5.2平行线的判定对应练习题及详解
文档属性
| 名称 | 5.2平行线的判定对应练习题及详解 |  | |
| 格式 | zip | ||
| 文件大小 | 298.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-13 20:57:07 | ||
图片预览



文档简介
2013.10.11平行线的判定
一.选择题(共29小题)
1.一个人从点A出发,沿北偏东70°的方向走到B处,再从点B处沿南偏西15°的方向走到点C处,那么∠ABC的度数是( )
A.55°B. 85°C. 105° D. 125°
2.下列说法中可能错误的是( )
A.过一点有且只有一条直线与已知直线平行 B. 过一点有且只有一条直线与已知直线垂直
C.两条直线相交,有且只有一个交点 D. 若两条直线相交成直角,则这两条直线互相垂直
3.下列说法正确的是( )
A. 两点之间的距离是两点间的线段 B. 与同一条直线垂直的两条直线也垂直 C. 同一平面内,过一点有且只有一条直线与已知直线平行
D. 同一平面内,过一点有且只有一条直线与已知直线垂直
4.下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( ) A.1个 B. 2个 C. 3个 D. 4个
5.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( ) A.∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
6.学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直线平行;④内错角相等,两直线平行.
A.①② B. ②③ C. ③④ D. ①④
7.有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A.2个 B. 3个 C. 4个 D. 5个
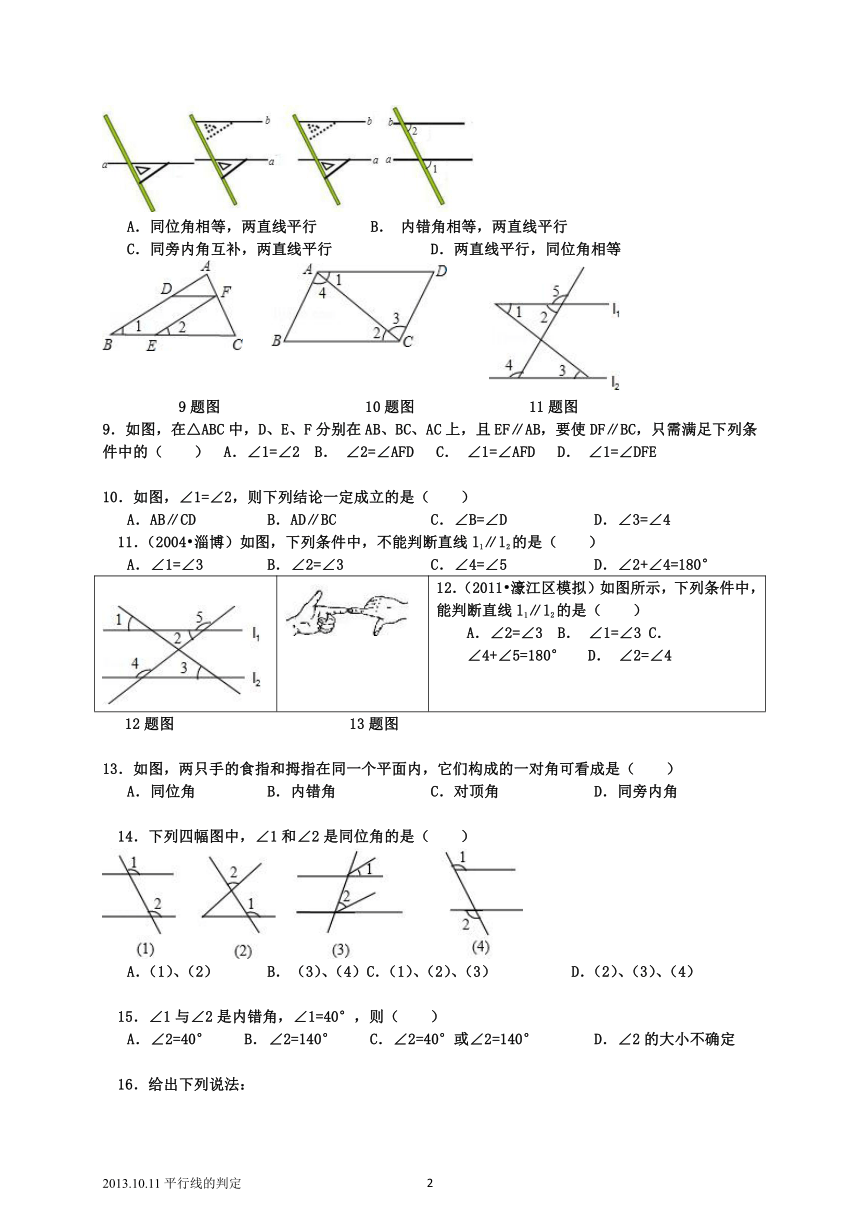
8.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B. 内错角相等,两直线平行
C.同旁内角互补,两直线平行 D. 两直线平行,同位角相等
9题图 10题图 11题图
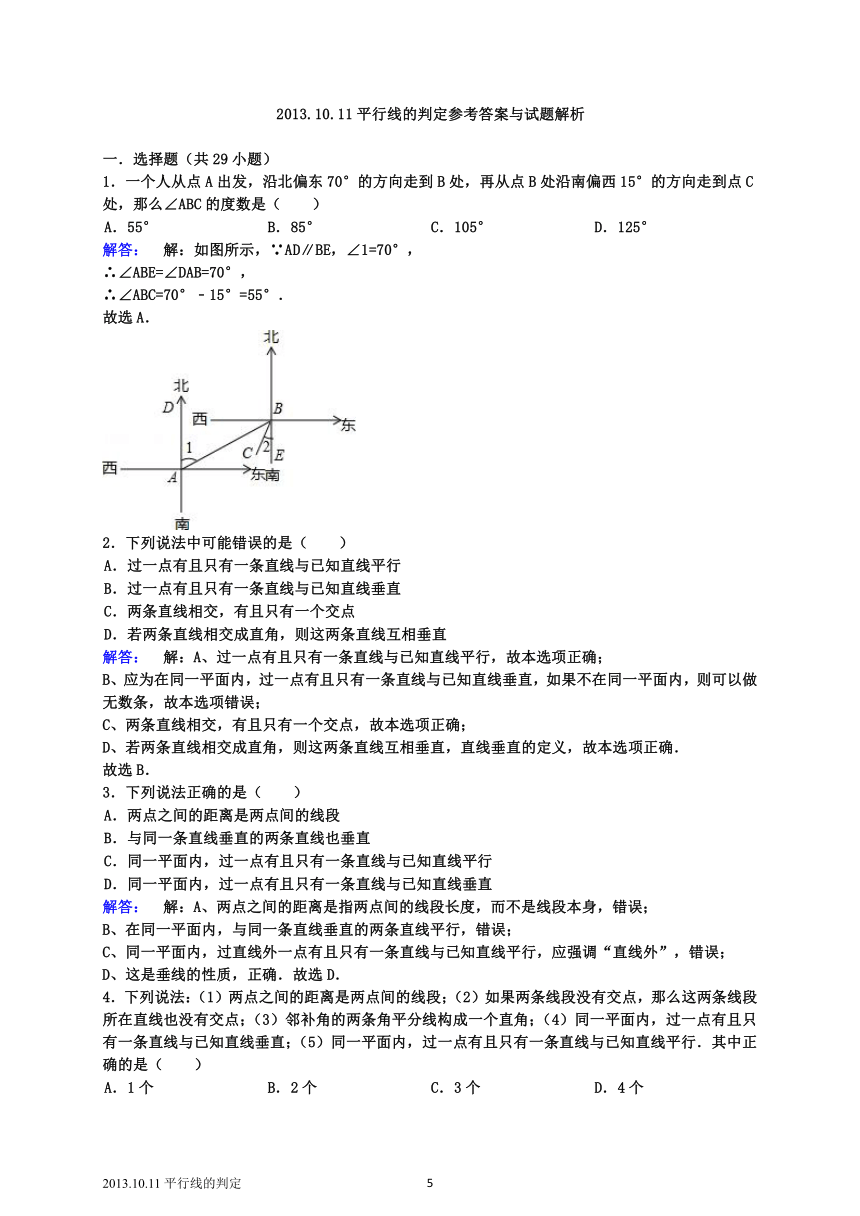
9.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的( ) A.∠1=∠2 B. ∠2=∠AFD C. ∠1=∠AFD D. ∠1=∠DFE
10.如图,∠1=∠2,则下列结论一定成立的是( )
A.AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
11.(2004 淄博)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B. ∠2=∠3 C. ∠4=∠5 D. ∠2+∠4=180°
12.(2011 濠江区模拟)如图所示,下列条件中,能判断直线l1∥l2的是( ) A.∠2=∠3 B. ∠1=∠3 C. ∠4+∠5=180° D. ∠2=∠4
12题图 13题图
13.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B. 内错角 C. 对顶角 D. 同旁内角
14.下列四幅图中,∠1和∠2是同位角的是( )
A.(1)、(2) B. (3)、(4)C.(1)、(2)、(3) D.(2)、(3)、(4)
15.∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40° B. ∠2=140° C.∠2=40°或∠2=140° D. ∠2的大小不确定
16.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( ) A.0个 B. 1个 C. 2个 D. 3个
17.下列所示的四个图形中,∠1和∠2是同位角的是( ) A.②③ B.①②③ C. ①②④ D①④
18.下列说法中正确的有( )个
①对顶角的角平分线成一条直线;②相邻二角的角平分线互相垂直;
③同旁内角的角平分线互相垂直;④邻补角的角平分线互相垂直. A.1B. 2 C. 3 D. 4
19.下列说法正确的是( ) A.同位角相等 B在同一平面内,如果a⊥b,b⊥c,则a⊥c C相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
20.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B. ∠3=∠4 C. ∠5=∠B D. ∠B+∠BDC=180°
20题图 21题图 22题图
21.如图,不能作为判断AB∥CD的条件是( )
A.∠FEB=∠ECD B. ∠AEC=∠ECD C. ∠BEC+∠ECD=180° D. ∠AEG=∠DCH
22.如图,在下列结论给出的条件中,不能判定AB∥DF的是( ) A.∠2+∠A=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A 23.如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( ) A.∠1=∠2 B. ∠B=∠DCE C. ∠3=∠4 D. ∠D+∠DAB=180°
24题图 25题图 27题图
24.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠3=∠4 D. ∠1=∠2
25.如图,要得到a∥b,则需要条件( )
A.∠2=∠4 B. ∠1+∠3=180° C. ∠1+∠2=180° D. ∠2=∠3
26.下面各语句中,正确的是( )
A. 两条直线被第三条直线所截,同位角相等 B. 垂直于同一条直线的两条直线平行
C. 若a∥b,c∥d,则a∥d D. 同旁内角互补,两直线平行
27.如图,点E在BC的延长线上,下列条件中能判断AB∥CD( )
A.∠3=∠4 B. ∠D=∠DCE C. ∠D+∠ACD=180° D. ∠1=∠2
28.下面的说法正确的个数为( )
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
A.1 B. 2 C. 3 D. 4
29.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
A. ①③ B. ②④ C. ①③④ D. ①②③④
二.填空题(共1小题)
30.下列说法:
(1)两点之间的所有连线中,线段最短;(2)相等的角是对顶角;(3)过一点有且仅有一条直线与已知直线平行;(4)长方体是四棱柱.其中正确的有 _________ (填正确说法的序号).
2013.10.11平行线的判定参考答案与试题解析
一.选择题(共29小题)
1.一个人从点A出发,沿北偏东70°的方向走到B处,再从点B处沿南偏西15°的方向走到点C处,那么∠ABC的度数是( )
A. 55° B. 85° C. 105° D. 125°
解答: 解:如图所示,∵AD∥BE,∠1=70°,
∴∠ABE=∠DAB=70°,
∴∠ABC=70°﹣15°=55°.
故选A.
2.下列说法中可能错误的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 过一点有且只有一条直线与已知直线垂直
C. 两条直线相交,有且只有一个交点
D. 若两条直线相交成直角,则这两条直线互相垂直
解答: 解:A、过一点有且只有一条直线与已知直线平行,故本选项正确;
B、应为在同一平面内,过一点有且只有一条直线与已知直线垂直,如果不在同一平面内,则可以做无数条,故本选项错误;
C、两条直线相交,有且只有一个交点,故本选项正确;
D、若两条直线相交成直角,则这两条直线互相垂直,直线垂直的定义,故本选项正确.
故选B.
3.下列说法正确的是( )
A. 两点之间的距离是两点间的线段
B. 与同一条直线垂直的两条直线也垂直
C. 同一平面内,过一点有且只有一条直线与已知直线平行
D. 同一平面内,过一点有且只有一条直线与已知直线垂直
解答: 解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,错误;
B、在同一平面内,与同一条直线垂直的两条直线平行,错误;
C、同一平面内,过直线外一点有且只有一条直线与已知直线平行,应强调“直线外”,错误;
D、这是垂线的性质,正确.故选D.
4.下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A. 1个 B. 2个 C. 3个 D. 4个
解答: 解:(1)两点之间的距离是两点间的线段长度,故(1)错误;
(2)如果两条线段没有交点,那么这两条线段所在直线不一定没有交点,故(2)错误;
(3)邻补角的两条角平分线一定构成一个直角,故(3)正确;
(4)同一平面内,过一点有且只有一条直线与已知直线垂直,故(4)正确;
(5)同一平面内,过直线外一点有且只有一条直线与已知直线平行,故(5)错误.
其中正确的是2个.故本题选B.
5.(2008 十堰)如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A. ∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
解答: 解:∵∠1=∠2,
∴BC∥AD(内错角相等,两直线平行).
故选C.
6.(2007 绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直线平行;④内错角相等,两直线平行.
A. ①② B. ②③ C. ③④ D. ①④
解答: 解:由作图过程可知,∠1=∠2,为内错角相等;∠1=∠4,为同位角相等;
可知小敏画平行线的依据有:③同位角相等,两直线平行;④内错角相等,两直线平行.
故选C.
7.(2006 梧州)有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
解答: 解:①忽略了两条直线必须是平行线;
③不应忽略相等的两个角的两条边必须互为反向延长线,才是对顶角;
④举一反例即可证明是错的:80°+60°=170°,170°显然不是锐角,故①③④是错的.
②是公理故正确;⑤根据补角定义如果两个角的和是一个平角,那么这两个角叫互为补角,
其中一个角叫做另一个角的补角,同角的补角相等.比如:∠A+∠B=180°,∠A+∠C=180°,则∠C=∠B. 等角的补角相等.比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D,则∠C=∠B.
∴②⑤是正确的.
故选A.
8.(2006 苏州)如图,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 两直线平行,同位角相等
考点: 平行线的判定.
专题: 作图题.
分析: 作图时保持∠1=∠2,则可判定两直线平行.
解答: 解:∵∠1=∠2,∴a∥b(同位角相等,两直线平行).故选A.
点评: 本题主要考查了平行线的判定.平行线的判定方法有:(1)定理1:同位角相等,两直线平行;(2)定理2:内错角相等,两直线平行;(3)定理3:同旁内角互补,两直线平行;(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行;(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
9.(2005 潍坊)如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的( )
A. ∠1=∠2 B. ∠2=∠AFD C. ∠1=∠AFD D. ∠1=∠DFE
考点: 平行线的判定.
分析: 要使DF∥BC,可围绕截线找同位角、内错角和同旁内角,选项中∠1=∠DFE,根据已知条件可得∠1=∠2,所以∠DFE=∠2,满足关于DF,BC的内错角相等,则DF∥BC.
解答: 解:∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).所以只需满足下列条件中的∠1=∠DFE.故选D.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.
10.(2005 双柏县)如图,∠1=∠2,则下列结论一定成立的是( )
A. AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
考点: 平行线的判定.
专题: 压轴题.
分析: 因为∠1与∠2是AD,BC被AC所截构成的内错角,所以结合已知,由内错角相等,两直线平行求解.
解答: 解:∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行).故选B.
点评: 正确识别同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
11.(2004 淄博)如图,下列条件中,不能判断直线l1∥l2的是( )
A. ∠1=∠3 B. ∠2=∠3 C. ∠4=∠5 D. ∠2+∠4=180°
考点: 平行线的判定.
分析: 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:∠1与∠3是l1与l2形成的内错角,所以能判断直线l1∥l2;∠4与∠5是l1与l2形成的同位角,所以能判断直线l1∥l2;∠2与∠4是l1与l2形成的同旁内角,所以能判断直线l1∥l2;∠2与∠3不是l1与l2形成的角,故不能判断直线l1∥l2.故选B.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两条被截直线平行.
12.(2011 濠江区模拟)如图所示,下列条件中,能判断直线l1∥l2的是( )
A. ∠2=∠3 B. ∠1=∠3 C. ∠4+∠5=180° D. ∠2=∠4
考点: 平行线的判定.
分析: 要证明两直线平行,则要找到同位角、内错角相等,同旁内角互补等.
解答: 解:A、∠2和∠3不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.B、∵∠1=∠3,∴l1∥l2(同位角相等两直线平行).C、∠4、∠5是直线l1、l2被第三条直线所截形成的同位角,故∠4+∠5=180°不能判断直线l1∥l2.D、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线l1∥l2.故选B.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
13.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A. 同位角 B. 内错角 C. 对顶角 D. 同旁内角
考点: 同位角、内错角、同旁内角.
分析: 拇指所在直线被两个食指所在的直线所截,因而构成的一对角可看成是内错角.
解答: 解:角在被截线的内部,又在截线的两侧,符合内错角的定义,故选B.
点评: 本题主要考查了内错角的定义.
14.下列四幅图中,∠1和∠2是同位角的是( )
A. (1)、(2) B. (3)、(4) C. (1)、(2)、(3) D. (2)、(3)、(4)
考点: 同位角、内错角、同旁内角.
分析: 互为同位角的两个角,都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
解答: 解:根据同位角的定义,图(1)、(2)中,∠1和∠2是同位角;图(3)∠1、∠2的两边都不在同一条直线上,不是同位角;图(4)∠1、∠2不在被截线同侧,不是同位角.故选A.
点评: 本题考查同位角的概念,是需要熟记的内容.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
15.∠1与∠2是内错角,∠1=40°,则( )
A. ∠2=40° B. ∠2=140° C. ∠2=40°或∠2=140° D. ∠2的大小不确定
考点: 同位角、内错角、同旁内角.
分析: 两直线平行时内错角相等,不平行时无法确定内错角的大小关系.
解答: 解:内错角只是一种位置关系,并没有一定的大小关系,只有两直线平行时,内错角才相等.故选D.
点评: 特别注意,内错角相等的条件是两直线平行.
16.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
考点: 同位角、内错角、同旁内角;对顶角、邻补角;点到直线的距离.
分析: 正确理解对顶角、同位角、相交线、平行线、点到直线的距离的概念,逐一判断.
解答: 解:(1)同位角只是一种位置关系,只有两条直线平行时,同位角相等,错误;(2)强调了在平面内,正确;(3)不符合对顶角的定义,错误;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段的本身,而是指垂线段的长度.故选B.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
17.下列所示的四个图形中,∠1和∠2是同位角的是( )
A. ②③ B. ①②③ C. ①②④ D. ①④
考点: 同位角、内错角、同旁内角.
分析: 此题在于考查同位角的概念,在截线的同侧,并且在被截线的同一方的两个角是同位角,所以①②④符合要求.
解答: 解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.
点评: 判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
18.下列说法中正确的有( )个
①对顶角的角平分线成一条直线;
②相邻二角的角平分线互相垂直;
③同旁内角的角平分线互相垂直;
④邻补角的角平分线互相垂直.
A. 1个 B. 2个 C. 3个 D. 4个
考点: 同位角、内错角、同旁内角;角平分线的定义;对顶角、邻补角.
分析: 本题考查几个类别图形的角平分线的关系,要从两个角的位置及大小上,进行判断.
解答: 解:①因为对顶角相等,其角平分线所分得的角也相等,可构成新的对顶角,故对顶角的角平分线成一条直线,正确;②相邻二角互补时角平分线互相垂直,其它情况下就不垂直,错误;③同旁内角互补时角平分线互相垂直,其它情况下就不垂直,错误;④由于邻补角互补,又有位置关系,故邻补角的角平分线互相垂直,正确.故选B.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
19.下列说法正确的是( )
A. 同位角相等 B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
考点: 平行公理及推论;对顶角、邻补角;平行线的判定.
分析: 根据平行线的性质和判定以及对顶角的定义进行判断.
解答: 解:A、只有在两直线平行这一前提下,同位角才相等,故错误;B、在同一平面内,如果a⊥b,b⊥c,则a∥c,所以B错误;C、相等的角不一定是对顶角,因为对顶角还有位置限制,所以C错误;D、由平行公理的推论知,D正确.故选D.
点评: 本题考查了平行线的性质、判定,对顶角的性质,注意对顶角一定相等,但相等的角不一定是对顶角.
20.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠B D. ∠B+∠BDC=180°
考点: 平行线的判定.
分析: 根据平行线的判定方法直接判定.
解答: 解:选项B中,∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),所以正确;选项C中,∵∠5=∠B,∴AB∥CD (内错角相等,两直线平行),所以正确;选项D中,∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),所以正确;而选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A错误.故选A.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
21.如图,不能作为判断AB∥CD的条件是( )
A. ∠FEB=∠ECD B. ∠AEC=∠ECD C. ∠BEC+∠ECD=180° D. ∠AEG=∠DCH
考点: 平行线的判定.
分析: 利用平行线的判定定理,逐一判断.
解答: 解:A、正确,∵∠FEB=∠ECD,∴AB∥CD(同位角相等,两直线平行).B、正确,∵∠AEC=∠ECD,∴AB∥CD(内错角相等,两直线平行).C、正确,∵∠BEC+∠ECD=180°,∴AB∥CD(同旁内角互补,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
22.如图,在下列结论给出的条件中,不能判定AB∥DF的是( )
A. ∠2+∠A=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A
考点: 平行线的判定.
分析: 利用平行线的判定定理,逐一判断.
解答: 解:A、∵∠2+∠A=180,∴AB∥DF(同旁内角互补,两直线平行);B、∵∠A=∠3,∴AB∥DF(同位角相等,两直线平行);C、∵∠1=∠4,∴AB∥DF(内错角相等,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
23.如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A. ∠1=∠2 B. ∠B=∠DCE C. ∠3=∠4 D. ∠D+∠DAB=180°
考点: 平行线的判定.
分析: 根据平行线的判定定理进行逐一分析解答即可.
解答: 解:A、正确,符合内错角相等,两条直线平行的判定定理;B、正确,符合同位角相等,两条直线平行的判定定理;C、错误,若∠3=∠4,则AD∥BE;D、正确,符合同旁内角互补,两条直线平行的判定定理;故选C.
点评: 本题考查的是平行线的判定定理,比较简单.
24.如图,下列条件中,能判定DE∥AC的是( )
A. ∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠3=∠4 D. ∠1=∠2
考点: 平行线的判定.
分析: 可以从直线DE、AC的截线所组成的“三线八角”图形入手进行判断.
解答: 解:∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行;∠AFE=∠ACD,∠1=∠2是EF和BC被AC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC;∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
25.如图,要得到a∥b,则需要条件( )
A. ∠2=∠4 B. ∠1+∠3=180° C. ∠1+∠2=180° D. ∠2=∠3
考点: 平行线的判定.
分析: 在复杂的图形中具有相等关系的两角要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:A、∵∠2=∠4,∴c∥d(同位角相等,两直线平行);B、∵∠1+∠3=180°,c∥d(同旁内角互补,两直线平行);C、∵∠1+∠2=180°,∴a∥b(同旁内角互补,两直线平行);D、∠2与∠3不能构成三线八角,无法判定两直线平行.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
26.下面各语句中,正确的是( )
A. 两条直线被第三条直线所截,同位角相等
B. 垂直于同一条直线的两条直线平行
C. 若a∥b,c∥d,则a∥d
D. 同旁内角互补,两直线平行
考点: 平行线的判定.
分析: 根据相关的定义或定理判断.
解答: 解:A、应强调两直线平行,被第三条直线所截,才能同位角相等;B、应强调在同一平面内,垂直于同一条直线的两条直线平行;C、应为a∥b,b∥c,c∥d,则a∥d;只有D正确.故选D.
点评: 叙述命题时要注意所学定理叙述的完整性,注意定理成立的条件.
27.如图,点E在BC的延长线上,下列条件中能判断AB∥CD( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠D+∠ACD=180° D. ∠1=∠2
考点: 平行线的判定.
分析: 根据平行线的判定定理对四个选项进行逐一分析即可.
解答: 解:A、错误,若∠3=∠4,则AC∥BD;B、错误,若∠D=∠DCE,则AC∥BD;C、错误,若∠D+∠ACD=180°,则AC∥BD;D、正确,若∠1=∠2,则AB∥CD.故选D.
点评: 此题比较简单,考查的是平行线的判定定理,解答此类题目的关键是正确区分两条直线被第三条直线所截形成的同位角、内错角及同旁内角.
28.下面的说法正确的个数为( )
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
A. 1 B. 2 C. 3 D. 4
考点: 平行线的判定;余角和补角;对顶角、邻补角.
分析: 根据相关的定义或定理,逐个进行判断,可知有2个是正确的,故选B.
解答: 解:①错误,不符合对顶角的定义.②正确,满足补角的定义.③正确,一个角的补角减去这个角的余角等于(180°﹣α)﹣(90°﹣α)=90°.④错误,同旁内角互补,两直线平行.故选B.
点评: 此题综合运用了对顶角、补角余角的定义和平行线的判定方法.
29.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
A. ①③ B. ②④ C. ①③④ D. ①②③④
考点: 平行线的判定;对顶角、邻补角.
分析: 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:①∵∠1=∠2,∴a∥b(同位角相等,两直线平行).②∵∠3=∠6,∴a∥b(内错角相等,两直线平行).③∵∠4+∠7=180°,∵∠4=∠6(对顶角相等),∴∠6+∠7=180°,∴a∥b(同旁内角互补,两直线平行).④同理得,a∥b(同旁内角互补,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
二.填空题(共1小题)
30.下列说法:
(1)两点之间的所有连线中,线段最短;(2)相等的角是对顶角;(3)过一点有且仅有一条直线与已知直线平行;(4)长方体是四棱柱.其中正确的有 (4) (填正确说法的序号).
考点: 平行公理及推论.
分析: 根据所学公理和性质解答.
解答: 解:(1)应为两点之间的所有连线中,直线段最短,故本说法错误;(2)相等的角不一定是对顶角,但对顶角相等,故本说法错误;(3)应为过直线外一点有且仅有一条直线与已知直线平行,故本说法错误;(4)长方体是四棱柱,正确.故正确的有(4).
点评: 本题是对数学语言的严谨性的考查,记忆数学公理、性质概念等一定要做的严谨.
PAGE
16
2013.10.11平行线的判定
一.选择题(共29小题)
1.一个人从点A出发,沿北偏东70°的方向走到B处,再从点B处沿南偏西15°的方向走到点C处,那么∠ABC的度数是( )
A.55°B. 85°C. 105° D. 125°
2.下列说法中可能错误的是( )
A.过一点有且只有一条直线与已知直线平行 B. 过一点有且只有一条直线与已知直线垂直
C.两条直线相交,有且只有一个交点 D. 若两条直线相交成直角,则这两条直线互相垂直
3.下列说法正确的是( )
A. 两点之间的距离是两点间的线段 B. 与同一条直线垂直的两条直线也垂直 C. 同一平面内,过一点有且只有一条直线与已知直线平行
D. 同一平面内,过一点有且只有一条直线与已知直线垂直
4.下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( ) A.1个 B. 2个 C. 3个 D. 4个
5.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( ) A.∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
6.学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直线平行;④内错角相等,两直线平行.
A.①② B. ②③ C. ③④ D. ①④
7.有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A.2个 B. 3个 C. 4个 D. 5个
8.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B. 内错角相等,两直线平行
C.同旁内角互补,两直线平行 D. 两直线平行,同位角相等
9题图 10题图 11题图
9.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的( ) A.∠1=∠2 B. ∠2=∠AFD C. ∠1=∠AFD D. ∠1=∠DFE
10.如图,∠1=∠2,则下列结论一定成立的是( )
A.AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
11.(2004 淄博)如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B. ∠2=∠3 C. ∠4=∠5 D. ∠2+∠4=180°
12.(2011 濠江区模拟)如图所示,下列条件中,能判断直线l1∥l2的是( ) A.∠2=∠3 B. ∠1=∠3 C. ∠4+∠5=180° D. ∠2=∠4
12题图 13题图
13.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B. 内错角 C. 对顶角 D. 同旁内角
14.下列四幅图中,∠1和∠2是同位角的是( )
A.(1)、(2) B. (3)、(4)C.(1)、(2)、(3) D.(2)、(3)、(4)
15.∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40° B. ∠2=140° C.∠2=40°或∠2=140° D. ∠2的大小不确定
16.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( ) A.0个 B. 1个 C. 2个 D. 3个
17.下列所示的四个图形中,∠1和∠2是同位角的是( ) A.②③ B.①②③ C. ①②④ D①④
18.下列说法中正确的有( )个
①对顶角的角平分线成一条直线;②相邻二角的角平分线互相垂直;
③同旁内角的角平分线互相垂直;④邻补角的角平分线互相垂直. A.1B. 2 C. 3 D. 4
19.下列说法正确的是( ) A.同位角相等 B在同一平面内,如果a⊥b,b⊥c,则a⊥c C相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
20.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B. ∠3=∠4 C. ∠5=∠B D. ∠B+∠BDC=180°
20题图 21题图 22题图
21.如图,不能作为判断AB∥CD的条件是( )
A.∠FEB=∠ECD B. ∠AEC=∠ECD C. ∠BEC+∠ECD=180° D. ∠AEG=∠DCH
22.如图,在下列结论给出的条件中,不能判定AB∥DF的是( ) A.∠2+∠A=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A 23.如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( ) A.∠1=∠2 B. ∠B=∠DCE C. ∠3=∠4 D. ∠D+∠DAB=180°
24题图 25题图 27题图
24.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠3=∠4 D. ∠1=∠2
25.如图,要得到a∥b,则需要条件( )
A.∠2=∠4 B. ∠1+∠3=180° C. ∠1+∠2=180° D. ∠2=∠3
26.下面各语句中,正确的是( )
A. 两条直线被第三条直线所截,同位角相等 B. 垂直于同一条直线的两条直线平行
C. 若a∥b,c∥d,则a∥d D. 同旁内角互补,两直线平行
27.如图,点E在BC的延长线上,下列条件中能判断AB∥CD( )
A.∠3=∠4 B. ∠D=∠DCE C. ∠D+∠ACD=180° D. ∠1=∠2
28.下面的说法正确的个数为( )
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
A.1 B. 2 C. 3 D. 4
29.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
A. ①③ B. ②④ C. ①③④ D. ①②③④
二.填空题(共1小题)
30.下列说法:
(1)两点之间的所有连线中,线段最短;(2)相等的角是对顶角;(3)过一点有且仅有一条直线与已知直线平行;(4)长方体是四棱柱.其中正确的有 _________ (填正确说法的序号).
2013.10.11平行线的判定参考答案与试题解析
一.选择题(共29小题)
1.一个人从点A出发,沿北偏东70°的方向走到B处,再从点B处沿南偏西15°的方向走到点C处,那么∠ABC的度数是( )
A. 55° B. 85° C. 105° D. 125°
解答: 解:如图所示,∵AD∥BE,∠1=70°,
∴∠ABE=∠DAB=70°,
∴∠ABC=70°﹣15°=55°.
故选A.
2.下列说法中可能错误的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 过一点有且只有一条直线与已知直线垂直
C. 两条直线相交,有且只有一个交点
D. 若两条直线相交成直角,则这两条直线互相垂直
解答: 解:A、过一点有且只有一条直线与已知直线平行,故本选项正确;
B、应为在同一平面内,过一点有且只有一条直线与已知直线垂直,如果不在同一平面内,则可以做无数条,故本选项错误;
C、两条直线相交,有且只有一个交点,故本选项正确;
D、若两条直线相交成直角,则这两条直线互相垂直,直线垂直的定义,故本选项正确.
故选B.
3.下列说法正确的是( )
A. 两点之间的距离是两点间的线段
B. 与同一条直线垂直的两条直线也垂直
C. 同一平面内,过一点有且只有一条直线与已知直线平行
D. 同一平面内,过一点有且只有一条直线与已知直线垂直
解答: 解:A、两点之间的距离是指两点间的线段长度,而不是线段本身,错误;
B、在同一平面内,与同一条直线垂直的两条直线平行,错误;
C、同一平面内,过直线外一点有且只有一条直线与已知直线平行,应强调“直线外”,错误;
D、这是垂线的性质,正确.故选D.
4.下列说法:(1)两点之间的距离是两点间的线段;(2)如果两条线段没有交点,那么这两条线段所在直线也没有交点;(3)邻补角的两条角平分线构成一个直角;(4)同一平面内,过一点有且只有一条直线与已知直线垂直;(5)同一平面内,过一点有且只有一条直线与已知直线平行.其中正确的是( )
A. 1个 B. 2个 C. 3个 D. 4个
解答: 解:(1)两点之间的距离是两点间的线段长度,故(1)错误;
(2)如果两条线段没有交点,那么这两条线段所在直线不一定没有交点,故(2)错误;
(3)邻补角的两条角平分线一定构成一个直角,故(3)正确;
(4)同一平面内,过一点有且只有一条直线与已知直线垂直,故(4)正确;
(5)同一平面内,过直线外一点有且只有一条直线与已知直线平行,故(5)错误.
其中正确的是2个.故本题选B.
5.(2008 十堰)如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A. ∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
解答: 解:∵∠1=∠2,
∴BC∥AD(内错角相等,两直线平行).
故选C.
6.(2007 绍兴)学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;②两直线平行,内错角相等;
③同位角相等,两直线平行;④内错角相等,两直线平行.
A. ①② B. ②③ C. ③④ D. ①④
解答: 解:由作图过程可知,∠1=∠2,为内错角相等;∠1=∠4,为同位角相等;
可知小敏画平行线的依据有:③同位角相等,两直线平行;④内错角相等,两直线平行.
故选C.
7.(2006 梧州)有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
解答: 解:①忽略了两条直线必须是平行线;
③不应忽略相等的两个角的两条边必须互为反向延长线,才是对顶角;
④举一反例即可证明是错的:80°+60°=170°,170°显然不是锐角,故①③④是错的.
②是公理故正确;⑤根据补角定义如果两个角的和是一个平角,那么这两个角叫互为补角,
其中一个角叫做另一个角的补角,同角的补角相等.比如:∠A+∠B=180°,∠A+∠C=180°,则∠C=∠B. 等角的补角相等.比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D,则∠C=∠B.
∴②⑤是正确的.
故选A.
8.(2006 苏州)如图,给出了过直线外一点画已知直线的平行线的方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 两直线平行,同位角相等
考点: 平行线的判定.
专题: 作图题.
分析: 作图时保持∠1=∠2,则可判定两直线平行.
解答: 解:∵∠1=∠2,∴a∥b(同位角相等,两直线平行).故选A.
点评: 本题主要考查了平行线的判定.平行线的判定方法有:(1)定理1:同位角相等,两直线平行;(2)定理2:内错角相等,两直线平行;(3)定理3:同旁内角互补,两直线平行;(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行;(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
9.(2005 潍坊)如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的( )
A. ∠1=∠2 B. ∠2=∠AFD C. ∠1=∠AFD D. ∠1=∠DFE
考点: 平行线的判定.
分析: 要使DF∥BC,可围绕截线找同位角、内错角和同旁内角,选项中∠1=∠DFE,根据已知条件可得∠1=∠2,所以∠DFE=∠2,满足关于DF,BC的内错角相等,则DF∥BC.
解答: 解:∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).所以只需满足下列条件中的∠1=∠DFE.故选D.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.
10.(2005 双柏县)如图,∠1=∠2,则下列结论一定成立的是( )
A. AB∥CD B. AD∥BC C. ∠B=∠D D. ∠3=∠4
考点: 平行线的判定.
专题: 压轴题.
分析: 因为∠1与∠2是AD,BC被AC所截构成的内错角,所以结合已知,由内错角相等,两直线平行求解.
解答: 解:∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行).故选B.
点评: 正确识别同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
11.(2004 淄博)如图,下列条件中,不能判断直线l1∥l2的是( )
A. ∠1=∠3 B. ∠2=∠3 C. ∠4=∠5 D. ∠2+∠4=180°
考点: 平行线的判定.
分析: 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:∠1与∠3是l1与l2形成的内错角,所以能判断直线l1∥l2;∠4与∠5是l1与l2形成的同位角,所以能判断直线l1∥l2;∠2与∠4是l1与l2形成的同旁内角,所以能判断直线l1∥l2;∠2与∠3不是l1与l2形成的角,故不能判断直线l1∥l2.故选B.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两条被截直线平行.
12.(2011 濠江区模拟)如图所示,下列条件中,能判断直线l1∥l2的是( )
A. ∠2=∠3 B. ∠1=∠3 C. ∠4+∠5=180° D. ∠2=∠4
考点: 平行线的判定.
分析: 要证明两直线平行,则要找到同位角、内错角相等,同旁内角互补等.
解答: 解:A、∠2和∠3不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.B、∵∠1=∠3,∴l1∥l2(同位角相等两直线平行).C、∠4、∠5是直线l1、l2被第三条直线所截形成的同位角,故∠4+∠5=180°不能判断直线l1∥l2.D、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2=∠4不能判断直线l1∥l2.故选B.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
13.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A. 同位角 B. 内错角 C. 对顶角 D. 同旁内角
考点: 同位角、内错角、同旁内角.
分析: 拇指所在直线被两个食指所在的直线所截,因而构成的一对角可看成是内错角.
解答: 解:角在被截线的内部,又在截线的两侧,符合内错角的定义,故选B.
点评: 本题主要考查了内错角的定义.
14.下列四幅图中,∠1和∠2是同位角的是( )
A. (1)、(2) B. (3)、(4) C. (1)、(2)、(3) D. (2)、(3)、(4)
考点: 同位角、内错角、同旁内角.
分析: 互为同位角的两个角,都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
解答: 解:根据同位角的定义,图(1)、(2)中,∠1和∠2是同位角;图(3)∠1、∠2的两边都不在同一条直线上,不是同位角;图(4)∠1、∠2不在被截线同侧,不是同位角.故选A.
点评: 本题考查同位角的概念,是需要熟记的内容.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
15.∠1与∠2是内错角,∠1=40°,则( )
A. ∠2=40° B. ∠2=140° C. ∠2=40°或∠2=140° D. ∠2的大小不确定
考点: 同位角、内错角、同旁内角.
分析: 两直线平行时内错角相等,不平行时无法确定内错角的大小关系.
解答: 解:内错角只是一种位置关系,并没有一定的大小关系,只有两直线平行时,内错角才相等.故选D.
点评: 特别注意,内错角相等的条件是两直线平行.
16.给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
考点: 同位角、内错角、同旁内角;对顶角、邻补角;点到直线的距离.
分析: 正确理解对顶角、同位角、相交线、平行线、点到直线的距离的概念,逐一判断.
解答: 解:(1)同位角只是一种位置关系,只有两条直线平行时,同位角相等,错误;(2)强调了在平面内,正确;(3)不符合对顶角的定义,错误;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,不是指点到直线的垂线段的本身,而是指垂线段的长度.故选B.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
17.下列所示的四个图形中,∠1和∠2是同位角的是( )
A. ②③ B. ①②③ C. ①②④ D. ①④
考点: 同位角、内错角、同旁内角.
分析: 此题在于考查同位角的概念,在截线的同侧,并且在被截线的同一方的两个角是同位角,所以①②④符合要求.
解答: 解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.
点评: 判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
18.下列说法中正确的有( )个
①对顶角的角平分线成一条直线;
②相邻二角的角平分线互相垂直;
③同旁内角的角平分线互相垂直;
④邻补角的角平分线互相垂直.
A. 1个 B. 2个 C. 3个 D. 4个
考点: 同位角、内错角、同旁内角;角平分线的定义;对顶角、邻补角.
分析: 本题考查几个类别图形的角平分线的关系,要从两个角的位置及大小上,进行判断.
解答: 解:①因为对顶角相等,其角平分线所分得的角也相等,可构成新的对顶角,故对顶角的角平分线成一条直线,正确;②相邻二角互补时角平分线互相垂直,其它情况下就不垂直,错误;③同旁内角互补时角平分线互相垂直,其它情况下就不垂直,错误;④由于邻补角互补,又有位置关系,故邻补角的角平分线互相垂直,正确.故选B.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
19.下列说法正确的是( )
A. 同位角相等 B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
考点: 平行公理及推论;对顶角、邻补角;平行线的判定.
分析: 根据平行线的性质和判定以及对顶角的定义进行判断.
解答: 解:A、只有在两直线平行这一前提下,同位角才相等,故错误;B、在同一平面内,如果a⊥b,b⊥c,则a∥c,所以B错误;C、相等的角不一定是对顶角,因为对顶角还有位置限制,所以C错误;D、由平行公理的推论知,D正确.故选D.
点评: 本题考查了平行线的性质、判定,对顶角的性质,注意对顶角一定相等,但相等的角不一定是对顶角.
20.如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠B D. ∠B+∠BDC=180°
考点: 平行线的判定.
分析: 根据平行线的判定方法直接判定.
解答: 解:选项B中,∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),所以正确;选项C中,∵∠5=∠B,∴AB∥CD (内错角相等,两直线平行),所以正确;选项D中,∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),所以正确;而选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A错误.故选A.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
21.如图,不能作为判断AB∥CD的条件是( )
A. ∠FEB=∠ECD B. ∠AEC=∠ECD C. ∠BEC+∠ECD=180° D. ∠AEG=∠DCH
考点: 平行线的判定.
分析: 利用平行线的判定定理,逐一判断.
解答: 解:A、正确,∵∠FEB=∠ECD,∴AB∥CD(同位角相等,两直线平行).B、正确,∵∠AEC=∠ECD,∴AB∥CD(内错角相等,两直线平行).C、正确,∵∠BEC+∠ECD=180°,∴AB∥CD(同旁内角互补,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
22.如图,在下列结论给出的条件中,不能判定AB∥DF的是( )
A. ∠2+∠A=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A
考点: 平行线的判定.
分析: 利用平行线的判定定理,逐一判断.
解答: 解:A、∵∠2+∠A=180,∴AB∥DF(同旁内角互补,两直线平行);B、∵∠A=∠3,∴AB∥DF(同位角相等,两直线平行);C、∵∠1=∠4,∴AB∥DF(内错角相等,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
23.如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是( )
A. ∠1=∠2 B. ∠B=∠DCE C. ∠3=∠4 D. ∠D+∠DAB=180°
考点: 平行线的判定.
分析: 根据平行线的判定定理进行逐一分析解答即可.
解答: 解:A、正确,符合内错角相等,两条直线平行的判定定理;B、正确,符合同位角相等,两条直线平行的判定定理;C、错误,若∠3=∠4,则AD∥BE;D、正确,符合同旁内角互补,两条直线平行的判定定理;故选C.
点评: 本题考查的是平行线的判定定理,比较简单.
24.如图,下列条件中,能判定DE∥AC的是( )
A. ∠EDC=∠EFC B. ∠AFE=∠ACD C. ∠3=∠4 D. ∠1=∠2
考点: 平行线的判定.
分析: 可以从直线DE、AC的截线所组成的“三线八角”图形入手进行判断.
解答: 解:∠EDC=∠EFC不是两直线被第三条直线所截得到的,因而不能判定两直线平行;∠AFE=∠ACD,∠1=∠2是EF和BC被AC所截得到的同位角和内错角,因而可以判定EF∥BC,但不能判定DE∥AC;∠3=∠4这两个角是AC与DE被EC所截得到的内错角,可以判定DE∥AC.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
25.如图,要得到a∥b,则需要条件( )
A. ∠2=∠4 B. ∠1+∠3=180° C. ∠1+∠2=180° D. ∠2=∠3
考点: 平行线的判定.
分析: 在复杂的图形中具有相等关系的两角要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:A、∵∠2=∠4,∴c∥d(同位角相等,两直线平行);B、∵∠1+∠3=180°,c∥d(同旁内角互补,两直线平行);C、∵∠1+∠2=180°,∴a∥b(同旁内角互补,两直线平行);D、∠2与∠3不能构成三线八角,无法判定两直线平行.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
26.下面各语句中,正确的是( )
A. 两条直线被第三条直线所截,同位角相等
B. 垂直于同一条直线的两条直线平行
C. 若a∥b,c∥d,则a∥d
D. 同旁内角互补,两直线平行
考点: 平行线的判定.
分析: 根据相关的定义或定理判断.
解答: 解:A、应强调两直线平行,被第三条直线所截,才能同位角相等;B、应强调在同一平面内,垂直于同一条直线的两条直线平行;C、应为a∥b,b∥c,c∥d,则a∥d;只有D正确.故选D.
点评: 叙述命题时要注意所学定理叙述的完整性,注意定理成立的条件.
27.如图,点E在BC的延长线上,下列条件中能判断AB∥CD( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠D+∠ACD=180° D. ∠1=∠2
考点: 平行线的判定.
分析: 根据平行线的判定定理对四个选项进行逐一分析即可.
解答: 解:A、错误,若∠3=∠4,则AC∥BD;B、错误,若∠D=∠DCE,则AC∥BD;C、错误,若∠D+∠ACD=180°,则AC∥BD;D、正确,若∠1=∠2,则AB∥CD.故选D.
点评: 此题比较简单,考查的是平行线的判定定理,解答此类题目的关键是正确区分两条直线被第三条直线所截形成的同位角、内错角及同旁内角.
28.下面的说法正确的个数为( )
①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.
A. 1 B. 2 C. 3 D. 4
考点: 平行线的判定;余角和补角;对顶角、邻补角.
分析: 根据相关的定义或定理,逐个进行判断,可知有2个是正确的,故选B.
解答: 解:①错误,不符合对顶角的定义.②正确,满足补角的定义.③正确,一个角的补角减去这个角的余角等于(180°﹣α)﹣(90°﹣α)=90°.④错误,同旁内角互补,两直线平行.故选B.
点评: 此题综合运用了对顶角、补角余角的定义和平行线的判定方法.
29.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
A. ①③ B. ②④ C. ①③④ D. ①②③④
考点: 平行线的判定;对顶角、邻补角.
分析: 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答: 解:①∵∠1=∠2,∴a∥b(同位角相等,两直线平行).②∵∠3=∠6,∴a∥b(内错角相等,两直线平行).③∵∠4+∠7=180°,∵∠4=∠6(对顶角相等),∴∠6+∠7=180°,∴a∥b(同旁内角互补,两直线平行).④同理得,a∥b(同旁内角互补,两直线平行).故选D.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
二.填空题(共1小题)
30.下列说法:
(1)两点之间的所有连线中,线段最短;(2)相等的角是对顶角;(3)过一点有且仅有一条直线与已知直线平行;(4)长方体是四棱柱.其中正确的有 (4) (填正确说法的序号).
考点: 平行公理及推论.
分析: 根据所学公理和性质解答.
解答: 解:(1)应为两点之间的所有连线中,直线段最短,故本说法错误;(2)相等的角不一定是对顶角,但对顶角相等,故本说法错误;(3)应为过直线外一点有且仅有一条直线与已知直线平行,故本说法错误;(4)长方体是四棱柱,正确.故正确的有(4).
点评: 本题是对数学语言的严谨性的考查,记忆数学公理、性质概念等一定要做的严谨.
PAGE
16
2013.10.11平行线的判定
