5.2平行线的判定对应练习及详解
文档属性
| 名称 | 5.2平行线的判定对应练习及详解 |  | |
| 格式 | zip | ||
| 文件大小 | 283.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-13 20:58:25 | ||
图片预览



文档简介
5.2平行线的判定
一.选择题(共8小题)
1.下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有( )
A.1个 B. 2个 C. 3个 D. 4个
2.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )
A.1个 B. 2个 C. 3个 D. 4个
3.根据图,下列推理判断错误的是( ) A.因为∠1=∠2,所以c∥d B. 因为∠3=∠4,所以c∥d C.因为∠1=∠3,所以c∥d D. 因为∠2=∠3,所以a∥b
3题图 4题图
4.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°,其中能说明a∥b的条件有( )个.
A.1 B. 2 C. 3 D. 4
5.有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A.2个 B. 3个 C. 4个 D. 5个
6.下列语句正确的是( )
A. 平角是直线 B. 画5cm长的射线 C. 平行线就是不相交的两条直线
D. 在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
7题图 8题图 7.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.A.4 B.8 C.12 D.168.图中所标出的角中,共有同位角( )A.2对 B. 3对 C. 4对 D. 5对
二.填空题(共6小题)
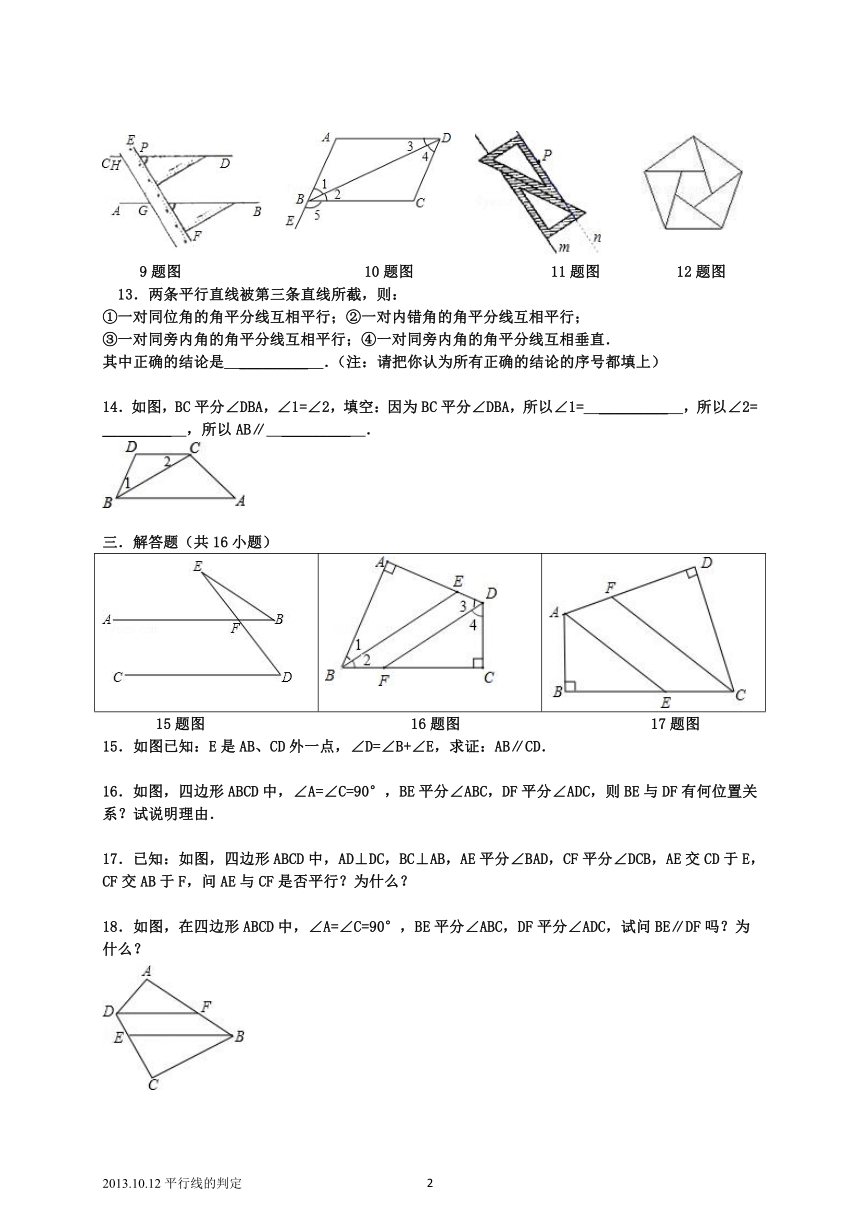
9.我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是 _________ .
10.如图:已知∠2=∠3,则 _________ ∥ _________ .
11.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是 _________ .
12.如图是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有 _________ 对平行线.
9题图 10题图 11题图 12题图
13.两条平行直线被第三条直线所截,则:
①一对同位角的角平分线互相平行;②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;④一对同旁内角的角平分线互相垂直.
其中正确的结论是 _________ .(注:请把你认为所有正确的结论的序号都填上)
14.如图,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1= _________ ,所以∠2= _________ ,所以AB∥ _________ .
三.解答题(共16小题)
15题图 16题图 17题图
15.如图已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.
16.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
17.已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
18.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?
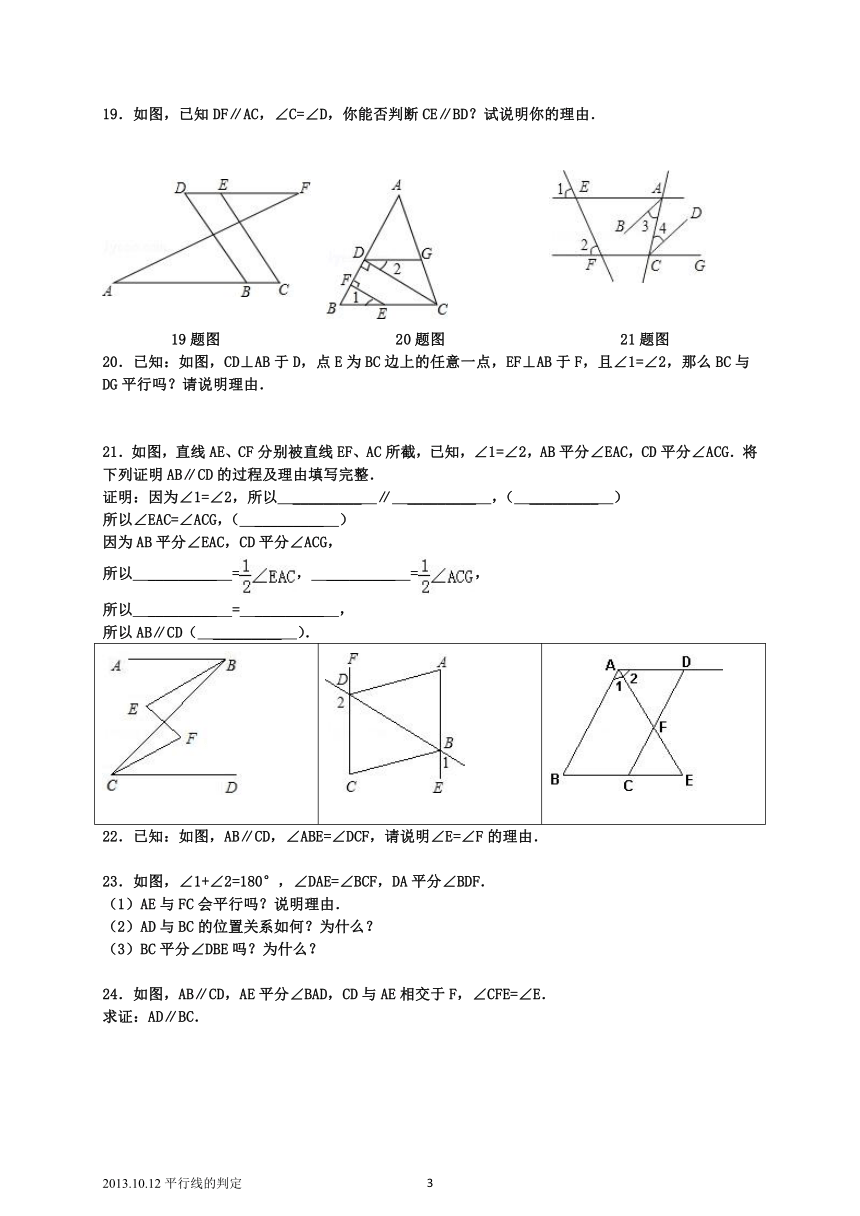
19.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
19题图 20题图 21题图
20.已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.
21.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:因为∠1=∠2,所以 _________ ∥ _________ ,( _________ )
所以∠EAC=∠ACG,( _________ )
因为AB平分∠EAC,CD平分∠ACG,
所以 _________ =, _________ =,
所以 _________ = _________ ,
所以AB∥CD( _________ ).
22.已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
23.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
求证:AD∥BC.
25.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
26.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
27.如图,∠1=30°,∠B=60°,AB⊥AC.①∠DAB+∠B=多少度?
②AD与BC平行吗?AB与CD平行吗?试说明理由.
28.如图,已知CD⊥AD,DA⊥AB,∠1=∠2.则DF与AE平行吗?为什么?
29.已知:如图在四边形ABCD中,∠A=∠D、∠B=∠C,试判断AD与BC的位置关系,并说明理由.
30.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
2013.10.115.2平行线的判定
参考答案与试题解析
一.选择题(共8小题)
1.下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 同位角、内错角、同旁内角;余角和补角;对顶角、邻补角.
分析: 根据内错角、对顶角、余角和补角的有关概念,逐一判断.
解答: 解:①内错角只是表示两个角的位置关系,只有当两直线平行时,内错角才相等,错误;②相等的角不一定具备对顶角的位置关系,故相等的角是对顶角,错误;③互余的两个角其和是90°,故每个角都小于90°,一定都是锐角,正确;④互补的两个角,有一种可能是两个角都是直角,不一定一个为钝角,另一个角为锐角,错误.故选A.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
2.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 平行线的判定.
分析: 根据对顶角的性质和平行线的判定定理,逐一判断.
解答: 解:①是正确的,对顶角相等;②正确,在同一平面内,垂直于同一条直线的两直线平行;③错误,角平分线分成的两个角相等但不是对顶角;④错误,同位角只有在两直线平行的情况下才相等.故①②正确,③④错误,所以错误的有两个,故选B.
点评: 平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要学会区分不同概念之间的联系和区别.
3.根据图,下列推理判断错误的是( )
A. 因为∠1=∠2,所以c∥d B. 因为∠3=∠4,所以c∥d
C. 因为∠1=∠3,所以c∥d D. 因为∠2=∠3,所以a∥b
考点: 平行线的判定.
分析: 根据平行线的判定定理进行解答.
解答: 解:A、正确,因为∠1=∠2,由内错角相等,两直线平行,所以c∥d;B、正确,因为∠3=∠4,由同位角相等,两直线平行,所以c∥d;C、三不符合平行线的判定条件,所以无法确定两直线平行.D、正确,因为∠2=∠3,由同位角相等,两直线平行,所以a∥b.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°,其中能说明a∥b的条件有( )个.
A. 1 B. 2 C. 3 D. 4
考点: 平行线的判定;对顶角、邻补角.
分析: 根据平行线的判定定理进行判断.同位角相等,两直线平行;内错角相等,两条直线平行;同旁内角互补,两条直线平行.
解答: 解:①根据同位角相等,两条直线平行.故此选项正确;②根据对顶角相等,得∠7=∠5,已知∠1=∠7,可得∠1=∠5,根据同位角相等,两条直线平行.故此选项正确;③根据内错角相等,两条直线平行.故此选项正确;④根据对顶角相等,得∠4=∠2,∠7=∠5,已知∠4+∠7=180°,可得∠2+∠5=180°,根据同旁内角互补,两直线平行.故此选项正确.故选D.
点评: 此题综合运用了对顶角相等的性质和平行线的判定方法.
5.(2006 梧州)有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
考点: 同位角、内错角、同旁内角;线段的性质:两点之间线段最短.
分析: 此题考查的知识点多,用平行线的性质,对顶角性质,补角的定义等来一一验证,从而求解.
解答: 解:①忽略了两条直线必须是平行线;③不应忽略相等的两个角的两条边必须互为反向延长线,才是对顶角;④举一反例即可证明是错的:80°+60°=170°,170°显然不是锐角,故①③④是错的.②是公理故正确;⑤根据补角定义如果两个角的和是一个平角,那么这两个角叫互为补角,其中一个角叫做另一个角的补角,同角的补角相等.比如:∠A+∠B=180°,∠A+∠C=180°,则∠C=∠B. 等角的补角相等.比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D,则∠C=∠B.∴②⑤是正确的.故选A.
点评: 此题涉及知识较多,请同学们认真阅读,最好借助图形来解答.
6.下列语句正确的是( )
A. 平角是直线
B. 画5cm长的射线
C. 平行线就是不相交的两条直线
D. 在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
考点: 平行线;直线、射线、线段;角的概念.
专题: 推理填空题.
分析: 根据角的定义即可判断A;根据射线的性质进行判断B;根据平行线的定义即可判断C;根据在同一平面内,两条不重合的直线的位置关系即可判断D.
解答: 解:A,根据角的定义,角是有公共端点的两条射线组成的图形,故本选项错误;B、射线没有长度,故本选项错误;C、平行线是指在同一平面内,不相交的直线,故本选项错误;D、在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行,故本选项正确.故选D.
点评: 本题主要考查对平行线的定义,射线的定义,角的定义等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
7.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
A. 4 B. 8 C. 12 D. 16
考点: 同位角、内错角、同旁内角.
专题: 分类讨论.
分析: 观察图形,确定不同的截线分类讨论,如分l1、l2被l3所截,l1、l2被l4所截,l1、l3被l4所截,l2、l3被l4所截,l3、l4被l1所截,l3、l4被l2所截l1、l4被l3所截、l2、l4被l3所截来讨论.
解答: 解:l1、l2被l3所截,有两对同旁内角,其它同理,故一共有同旁内角2×8=16对.故选D.
点评: 在较复杂图形中确定“三线八角”可从截线入手,分类讨论,做到不重复不遗漏.
8.图中所标出的角中,共有同位角( )
A. 2对 B. 3对 C. 4对 D. 5对
考点: 同位角、内错角、同旁内角.
分析: 本题考查同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
解答: 解:根据同位角的定义,图中∠3与∠4,∠4与∠5,∠7与∠1,∠5与∠2,∠2与∠3是同位角,共5对.故选D.
点评: 判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
二.填空题(共6小题)
9.我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是 同位角相等,两直线平行 .
考点: 平行线的判定.
分析: 由已知可知∠DPF=∠BMF,从而得出同位角相等,两直线平行.
解答: 解:∵∠DPF=∠BMF,∴AB∥CD(同位角相等,两直线平行).
点评: 正确理解题目的含义,是解决本题的关键.
10.如图:已知∠2=∠3,则 AD ∥ BC .
考点: 平行线的判定.
分析: 因为∠2=∠3,在图中发现AD、BC被BD所截,故可按内错角相等两直线平行进行判定.
解答: 解:∵∠2=∠3,∴AD∥BC(内错角相等两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题能有效地培养“执果索图”的思维方式与能力.
11.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是 内错角相等,两直线平行 .
考点: 平行线的判定.
专题: 应用题.
分析: 根据图形知道已知∠PAB=∠ACD,利用内错角相等,判断两直线平行.
解答: 解:∵∠PAB=∠ACD,∴CD∥AP(内错角相等,两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索图”的思维方式与能力.
12.如图是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有 5 对平行线.
考点: 平行线的判定.
分析: 利用平行线的判定,由已知角相等或互补推出两直线平行.
解答: 解:∵∠BAG=∠AHE=72°,∴AB∥EI;∵∠BFC=∠FCD=72°,∴BG∥CD;∵∠CBF=∠BGA=72°,∴BC∥AH;∵∠EDI=∠CKD=72°,∴DE∥CF;∵∠AEH=∠EID=72°,∴AE∥DK.故共有5对平行线.
点评: 本题是考查平行线的判定的基础题,比较容易.
13.两条平行直线被第三条直线所截,则:
①一对同位角的角平分线互相平行;
②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;
④一对同旁内角的角平分线互相垂直.
其中正确的结论是 ①②④ .(注:请把你认为所有正确的结论的序号都填上)
考点: 平行线的判定.
分析: 根据平行线的性质,结合图形分析平分角之后得到的角之间的位置关系,运用平行线的判定判断是否平行;若不平行,则进一步探究其特殊性.
解答: 解:①两直线平行,同位角相等,其角平分线分得的角也相等.根据同位角相等,两直线平行可判断角平分线平行;②两直线平行,内错角相等,其角平分线分得的角也相等.根据内错角相等,两直线平行可判断角平分线平行;③显然不对;④两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直.故正确的结论是①②④.
点评: 本题考查的是平行线的性质和判定.
14.如图,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1= ∠CBA ,所以∠2= ∠CBA ,所以AB∥ CD .
考点: 平行线的判定;角平分线的定义.
分析: 由角平分线的性质可知∠1=∠CBA,由内错角相等,两直线平行可知AB∥CD.
解答: 解:∵BC平分∠DBA,∴∠1=∠CBA,又∵∠1=∠2,∴∠2=∠CBA,∴AB∥CD(内错角相等,两直线平行).
点评: 此题主要考查了角平分线的性质及内错角相等,两直线平行的判定定理.
三.解答题(共16小题)
15.已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.
考点: 三角形的外角性质;平行线的判定.
专题: 证明题.
分析: 欲证AB∥CD,已知∠D=∠B+∠E,且∠BFD=∠B+∠E,即证∴∠D=∠BFD,故可根据内错角相等,两直线平行求证.
解答: 证明:∵∠D=∠B+∠E(已知),∠BFD=∠B+∠E(三角形的一个外角等于与它不相留邻的两个内角的和),∴∠D=∠BFD(等式的性质).∴AB∥CD(内错角相等,两直线平行).
点评: 本题考查的是三角形内角与外角的关系及两直线平行判定定理,比较简单.三角形的一个外角等于和它不相邻的两个内角和.同位角相等、内错角相等、同旁内角互补,两直线平行.
16.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
考点: 平行线的判定;角平分线的定义.
专题: 探究型.
分析: 根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
解答: 解:BE∥DF.理由如下:∵∠A=∠C=90°(已知),∴∠ABC+∠ADC=180°(四边形的内角和等于360°).∵BE平分∠ABC,DF平分∠ADC,∴∠1=∠2=∠ABC,∠3=∠4=∠ADC(角平分线的定义).∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°(等式的性质).又∠1+∠AEB=90°(三角形的内角和等于180°),∴∠3=∠AEB(等量代换).∴BE∥DF(同位角相等,两直线平行).
点评: 此题运用了四边形的内角和定理、角平分线定义、等角的余角相等和平行线的判定,难度中等.
17.已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: 想证明AE与CF平行需构造应用平行线判定方法的条件,∠DEA和∠DFC是直线AE与FC被直线CD所截而成的同位角,根据垂直的定义和角平分线的性质可结合图形证得∠DAE=∠DFC,再根据同位角相等,两直线平行可得AE∥CF.
解答: 解:平行.理由如下:∵AD⊥DC,BC⊥AB,∴∠D=∠B=90°.∵∠DAB+∠B+∠BCD+∠D=360°,∴∠DAB+∠BCD=180°.∵AE平分∠BAD,CF平分∠DCB,∴∠DAE+∠DCF=90°.∵∠D+∠DFC+∠DCF=180°,∴∠DFC+∠DCF=90°.∴∠DAE=∠DFC∴AE∥CF.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.本题通过构造同位角相等证明两被截直线平行.
18.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?
考点: 平行线的判定;多边形内角与外角.
专题: 探究型.
分析: 要证BE∥DF,需证∠FDC=∠BEC,由于已知里给出了两条角平分线,ABCD又是四边形,内角和为360°,可得:∠FDC+∠EBC=90°,在△BCE中,∠BEC+∠EBC=90°,等角的余角相等,就可得到∠FDC=∠BEC,即可证.
解答: 解:平行.∵∠A=∠C=90°,四边形ABCD的内角和为360°,∴∠ADC+∠ABC=180°,∵BE平分∠ABC,DF平分∠ADC,∴∠FDC+∠EBC=90°.又∵∠C=90°,∴∠BEC+∠EBC=90°,∴∠FDC=∠BEC,∴BE∥DF.
点评: 本题利用了角平分线性质和判定,四边形的内角和为360°,同角的余角相等.
19.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
考点: 平行线的判定.
专题: 探究型.
分析: 因为DF∥AC,由内错角相等证明∠C=∠FEC,又因为∠C=∠D,则∠D=∠FEC,故CE∥BD.
解答: 解:CE∥BD.理由:∵DF∥AC(已知),∴∠C=∠FEC(两直线平行,内错角相等),又∵∠C=∠D(已知),∴∠D=∠FEC(等量代换),∴CE∥BD(同位角相等,两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题能有效地培养“执果索图”的思维方式与能力.
20.已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.
考点: 平行线的判定.
专题: 探究型.
分析: 要说明BC∥DG,需先确定与两直线都相交的第三线.图中有三条AB、AC、CD,很显然利用DC更为方便,在“三线八角”中,与已知∠1、∠2都相关的角为∠DCB.至此,证题途径已经明朗.
解答: 解:∵CD⊥AB,EF⊥AB,∴CD∥EF;∴∠1=∠BCD(两直线平行,同位角相等);又∵∠1=∠2(已知),∴∠2=∠BCD;∴BC∥DG(内错角相等,两直线平行).
点评: 本题主要考查了平行线的性质和判定.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角的关系.
21.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:因为∠1=∠2,所以 AE ∥ CF ,( 同位角相等,两直线平行 )
所以∠EAC=∠ACG,( 两直线平行,内错角相等 )
因为AB平分∠EAC,CD平分∠ACG,
所以 ∠3 =, ∠4 =,
所以 ∠3 = ∠4 ,
所以AB∥CD( 内错角相等,两直线平行 ).
考点: 平行线的判定.
专题: 推理填空题.
分析: 利用平行线的判定及性质就可求得本题.即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.反之即为性质.
解答: 证明:因为∠1=∠2,所以AE∥CF(同位角相等,两直线平行),所以∠EAC=∠ACG(两直线平行,内错角相等),因为AB平分∠EAC,CD平分∠ACG,所以∠3=,∠4=,所以∠3=∠4,所以AB∥CD(内错角相等,两直线平行).
点评: 此题主要考查了平行线的判定即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线的判定即两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.
22.已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
考点: 平行线的判定.
专题: 证明题.
分析: 根据两直线平行内错角相等可得,∠ABC=∠BCD结合已知又可知∠EBC=∠FCB,所以BE∥CF(内错角相等,两直线平行)从而证两角相等.
解答: 解:∵AB∥CD(已知),∴∠ABC=∠BCD(两直线平行内错角相等),∵∠ABE=∠DCF(已知),∴∠EBC=∠FCB,∴BE∥CF(内错角相等,两直线平行),∴∠E=∠F(两直线平行内错角相等).
点评: 本题主要利用平行线的性质和判定及图中角的和差关系来证明.
23.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: (1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.
解答: 解:(1)平行,证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索图”的思维方式与能力.
24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
求证:AD∥BC.
考点: 平行线的判定.
专题: 证明题.
分析: 首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.
解答: 证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.
点评: 本题考查角平分线的性质以及平行线的判定定理.
25.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
考点: 平行线的判定.
专题: 证明题.
分析: 先由已知证明AD∥EF,再证明1∠1=∠4,∠2=∠4,等量代换得出∠1=∠2.
解答: 证明:∵AD⊥BC,EF⊥BC(已知),∴AD∥EF(垂直于同一条直线的两直线平行),∴∠1=∠4(两直线平行,同位角相等),又∵∠3=∠C(已知),∴AC∥DG(同位角相等,两直线平行),∴∠2=∠4(两直线平行,内错角相等),∴∠1=∠2(等量代换).
点评: 此题的关键是理解平行线的性质及判定.①两直线平行,同位角相等.②两直线平行,内错角相等.③同位角相等,两直线平行.④内错角相等,两直线平行.
26.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
考点: 平行线的判定.
专题: 探究型.
分析: 设AB与DE相交于H,若判断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.
解答: 解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,又∵∠5=∠6,∴∠BAF=∠6,∴AB∥CD,∴∠2=∠EHA,又∵∠1=∠2,即∠1=∠EHA,∴BF∥DE.另解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,∵∠5=∠6,∴∠BAF=∠6,∵△BFA、△DEC的内角和都是180°∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6∵∠1=∠2;∠BAF=∠6∴∠BFA=∠4(同位角相等,两直线就平行)∴BF∥DE.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
27.如图,∠1=30°,∠B=60°,AB⊥AC.
①∠DAB+∠B=多少度?
②AD与BC平行吗?AB与CD平行吗?试说明理由.
考点: 平行线的判定.
专题: 探究型.
分析: (1)由已知可求得∠DAB=120°,从而可求得∠DAB+∠B=180°(2)根据同旁内角互补两直线平行可得AD∥BC,∠ACD不能确定从而不能确定AB与CD平行.
解答: 解:①∵AB⊥AC,∴∠BAC=90°,又∠1=30°,∴∠BAD=120°,∵∠B=60°,∴∠DAB+∠B=180°(7分).②答:AD∥BC,AB与CD不一定平行.(3分)理由是:∵∠DAB+∠B=180°∴AD∥BC(4分)∵∠ACD不能确定(5分)∴AB与CD不一定平行.(6分)
点评: 此题主要考查学生对平行线的判定的理解及运用.
28.如图,已知CD⊥AD,DA⊥AB,∠1=∠2.则DF与AE平行吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: DF和AE的截线是AD,欲证FD∥AE,需证∠FDA=∠DAE,由已知条件易得此结论.
解答: 解:FD∥AE.理由如下:∵CD⊥AD,DA⊥AB,∴∠2+∠FDA=90°,∠1+∠DAE=90°,又∠1=∠2,∴∠FDA=∠DAE,∴FD∥AE(内错角相等,两直线平行).
点评: 本题利用了等角的余角相等,还有平行线的判定:内错角相等,两直线平行.
29.已知:如图在四边形ABCD中,∠A=∠D、∠B=∠C,试判断AD与BC的位置关系,并说明理由.
考点: 平行线的判定.
分析: 根据四边形ABCD的内角和是360°,结合已知条件得到∠A+∠B=180°,根据同旁内角互补,两直线平行得AD∥BC.
解答: 解:AD与BC的位置关系是平行.理由:∵四边形ABCD的内角和是360°,∴∠A+∠B+∠C+∠D=360°,∵∠A=∠D,∠B=∠C,∴∠A+∠B+∠B+∠A=360°,∴∠A+∠B=180°,∴AD∥BC(同旁内角互补,两直线平行).
点评: 本题考查四边形的内角和以及利用同旁内角互补,两直线平行进行解答.
30.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: 本题可通过证直线EF与BD的内错角∠1和∠2相等,来得出EF∥BD的结论.
解答: 解:EF∥BD;理由如下:∵∠AED=60°,EF平分∠AED,∴∠FED=30°,又∵∠FEB=∠2=30°,∴EF∥BD(内错角相等,两直线平行).
点评: 本题主要考查了平行线的判定方法:内错角相等,两直线平行.
PAGE
20
2013.10.12平行线的判定
一.选择题(共8小题)
1.下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有( )
A.1个 B. 2个 C. 3个 D. 4个
2.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )
A.1个 B. 2个 C. 3个 D. 4个
3.根据图,下列推理判断错误的是( ) A.因为∠1=∠2,所以c∥d B. 因为∠3=∠4,所以c∥d C.因为∠1=∠3,所以c∥d D. 因为∠2=∠3,所以a∥b
3题图 4题图
4.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°,其中能说明a∥b的条件有( )个.
A.1 B. 2 C. 3 D. 4
5.有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A.2个 B. 3个 C. 4个 D. 5个
6.下列语句正确的是( )
A. 平角是直线 B. 画5cm长的射线 C. 平行线就是不相交的两条直线
D. 在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
7题图 8题图 7.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.A.4 B.8 C.12 D.168.图中所标出的角中,共有同位角( )A.2对 B. 3对 C. 4对 D. 5对
二.填空题(共6小题)
9.我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是 _________ .
10.如图:已知∠2=∠3,则 _________ ∥ _________ .
11.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是 _________ .
12.如图是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有 _________ 对平行线.
9题图 10题图 11题图 12题图
13.两条平行直线被第三条直线所截,则:
①一对同位角的角平分线互相平行;②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;④一对同旁内角的角平分线互相垂直.
其中正确的结论是 _________ .(注:请把你认为所有正确的结论的序号都填上)
14.如图,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1= _________ ,所以∠2= _________ ,所以AB∥ _________ .
三.解答题(共16小题)
15题图 16题图 17题图
15.如图已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.
16.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
17.已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
18.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?
19.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
19题图 20题图 21题图
20.已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.
21.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:因为∠1=∠2,所以 _________ ∥ _________ ,( _________ )
所以∠EAC=∠ACG,( _________ )
因为AB平分∠EAC,CD平分∠ACG,
所以 _________ =, _________ =,
所以 _________ = _________ ,
所以AB∥CD( _________ ).
22.已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
23.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
求证:AD∥BC.
25.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
26.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
27.如图,∠1=30°,∠B=60°,AB⊥AC.①∠DAB+∠B=多少度?
②AD与BC平行吗?AB与CD平行吗?试说明理由.
28.如图,已知CD⊥AD,DA⊥AB,∠1=∠2.则DF与AE平行吗?为什么?
29.已知:如图在四边形ABCD中,∠A=∠D、∠B=∠C,试判断AD与BC的位置关系,并说明理由.
30.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
2013.10.115.2平行线的判定
参考答案与试题解析
一.选择题(共8小题)
1.下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 同位角、内错角、同旁内角;余角和补角;对顶角、邻补角.
分析: 根据内错角、对顶角、余角和补角的有关概念,逐一判断.
解答: 解:①内错角只是表示两个角的位置关系,只有当两直线平行时,内错角才相等,错误;②相等的角不一定具备对顶角的位置关系,故相等的角是对顶角,错误;③互余的两个角其和是90°,故每个角都小于90°,一定都是锐角,正确;④互补的两个角,有一种可能是两个角都是直角,不一定一个为钝角,另一个角为锐角,错误.故选A.
点评: 对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
2.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
考点: 平行线的判定.
分析: 根据对顶角的性质和平行线的判定定理,逐一判断.
解答: 解:①是正确的,对顶角相等;②正确,在同一平面内,垂直于同一条直线的两直线平行;③错误,角平分线分成的两个角相等但不是对顶角;④错误,同位角只有在两直线平行的情况下才相等.故①②正确,③④错误,所以错误的有两个,故选B.
点评: 平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要学会区分不同概念之间的联系和区别.
3.根据图,下列推理判断错误的是( )
A. 因为∠1=∠2,所以c∥d B. 因为∠3=∠4,所以c∥d
C. 因为∠1=∠3,所以c∥d D. 因为∠2=∠3,所以a∥b
考点: 平行线的判定.
分析: 根据平行线的判定定理进行解答.
解答: 解:A、正确,因为∠1=∠2,由内错角相等,两直线平行,所以c∥d;B、正确,因为∠3=∠4,由同位角相等,两直线平行,所以c∥d;C、三不符合平行线的判定条件,所以无法确定两直线平行.D、正确,因为∠2=∠3,由同位角相等,两直线平行,所以a∥b.故选C.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°,其中能说明a∥b的条件有( )个.
A. 1 B. 2 C. 3 D. 4
考点: 平行线的判定;对顶角、邻补角.
分析: 根据平行线的判定定理进行判断.同位角相等,两直线平行;内错角相等,两条直线平行;同旁内角互补,两条直线平行.
解答: 解:①根据同位角相等,两条直线平行.故此选项正确;②根据对顶角相等,得∠7=∠5,已知∠1=∠7,可得∠1=∠5,根据同位角相等,两条直线平行.故此选项正确;③根据内错角相等,两条直线平行.故此选项正确;④根据对顶角相等,得∠4=∠2,∠7=∠5,已知∠4+∠7=180°,可得∠2+∠5=180°,根据同旁内角互补,两直线平行.故此选项正确.故选D.
点评: 此题综合运用了对顶角相等的性质和平行线的判定方法.
5.(2006 梧州)有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
考点: 同位角、内错角、同旁内角;线段的性质:两点之间线段最短.
分析: 此题考查的知识点多,用平行线的性质,对顶角性质,补角的定义等来一一验证,从而求解.
解答: 解:①忽略了两条直线必须是平行线;③不应忽略相等的两个角的两条边必须互为反向延长线,才是对顶角;④举一反例即可证明是错的:80°+60°=170°,170°显然不是锐角,故①③④是错的.②是公理故正确;⑤根据补角定义如果两个角的和是一个平角,那么这两个角叫互为补角,其中一个角叫做另一个角的补角,同角的补角相等.比如:∠A+∠B=180°,∠A+∠C=180°,则∠C=∠B. 等角的补角相等.比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D,则∠C=∠B.∴②⑤是正确的.故选A.
点评: 此题涉及知识较多,请同学们认真阅读,最好借助图形来解答.
6.下列语句正确的是( )
A. 平角是直线
B. 画5cm长的射线
C. 平行线就是不相交的两条直线
D. 在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
考点: 平行线;直线、射线、线段;角的概念.
专题: 推理填空题.
分析: 根据角的定义即可判断A;根据射线的性质进行判断B;根据平行线的定义即可判断C;根据在同一平面内,两条不重合的直线的位置关系即可判断D.
解答: 解:A,根据角的定义,角是有公共端点的两条射线组成的图形,故本选项错误;B、射线没有长度,故本选项错误;C、平行线是指在同一平面内,不相交的直线,故本选项错误;D、在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行,故本选项正确.故选D.
点评: 本题主要考查对平行线的定义,射线的定义,角的定义等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
7.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
A. 4 B. 8 C. 12 D. 16
考点: 同位角、内错角、同旁内角.
专题: 分类讨论.
分析: 观察图形,确定不同的截线分类讨论,如分l1、l2被l3所截,l1、l2被l4所截,l1、l3被l4所截,l2、l3被l4所截,l3、l4被l1所截,l3、l4被l2所截l1、l4被l3所截、l2、l4被l3所截来讨论.
解答: 解:l1、l2被l3所截,有两对同旁内角,其它同理,故一共有同旁内角2×8=16对.故选D.
点评: 在较复杂图形中确定“三线八角”可从截线入手,分类讨论,做到不重复不遗漏.
8.图中所标出的角中,共有同位角( )
A. 2对 B. 3对 C. 4对 D. 5对
考点: 同位角、内错角、同旁内角.
分析: 本题考查同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
解答: 解:根据同位角的定义,图中∠3与∠4,∠4与∠5,∠7与∠1,∠5与∠2,∠2与∠3是同位角,共5对.故选D.
点评: 判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.
二.填空题(共6小题)
9.我们可以用直尺和三角尺画平行线,如图,在这一过程中,所用到的判断两直线平行的方法是 同位角相等,两直线平行 .
考点: 平行线的判定.
分析: 由已知可知∠DPF=∠BMF,从而得出同位角相等,两直线平行.
解答: 解:∵∠DPF=∠BMF,∴AB∥CD(同位角相等,两直线平行).
点评: 正确理解题目的含义,是解决本题的关键.
10.如图:已知∠2=∠3,则 AD ∥ BC .
考点: 平行线的判定.
分析: 因为∠2=∠3,在图中发现AD、BC被BD所截,故可按内错角相等两直线平行进行判定.
解答: 解:∵∠2=∠3,∴AD∥BC(内错角相等两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题能有效地培养“执果索图”的思维方式与能力.
11.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是 内错角相等,两直线平行 .
考点: 平行线的判定.
专题: 应用题.
分析: 根据图形知道已知∠PAB=∠ACD,利用内错角相等,判断两直线平行.
解答: 解:∵∠PAB=∠ACD,∴CD∥AP(内错角相等,两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索图”的思维方式与能力.
12.如图是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有 5 对平行线.
考点: 平行线的判定.
分析: 利用平行线的判定,由已知角相等或互补推出两直线平行.
解答: 解:∵∠BAG=∠AHE=72°,∴AB∥EI;∵∠BFC=∠FCD=72°,∴BG∥CD;∵∠CBF=∠BGA=72°,∴BC∥AH;∵∠EDI=∠CKD=72°,∴DE∥CF;∵∠AEH=∠EID=72°,∴AE∥DK.故共有5对平行线.
点评: 本题是考查平行线的判定的基础题,比较容易.
13.两条平行直线被第三条直线所截,则:
①一对同位角的角平分线互相平行;
②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;
④一对同旁内角的角平分线互相垂直.
其中正确的结论是 ①②④ .(注:请把你认为所有正确的结论的序号都填上)
考点: 平行线的判定.
分析: 根据平行线的性质,结合图形分析平分角之后得到的角之间的位置关系,运用平行线的判定判断是否平行;若不平行,则进一步探究其特殊性.
解答: 解:①两直线平行,同位角相等,其角平分线分得的角也相等.根据同位角相等,两直线平行可判断角平分线平行;②两直线平行,内错角相等,其角平分线分得的角也相等.根据内错角相等,两直线平行可判断角平分线平行;③显然不对;④两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直.故正确的结论是①②④.
点评: 本题考查的是平行线的性质和判定.
14.如图,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1= ∠CBA ,所以∠2= ∠CBA ,所以AB∥ CD .
考点: 平行线的判定;角平分线的定义.
分析: 由角平分线的性质可知∠1=∠CBA,由内错角相等,两直线平行可知AB∥CD.
解答: 解:∵BC平分∠DBA,∴∠1=∠CBA,又∵∠1=∠2,∴∠2=∠CBA,∴AB∥CD(内错角相等,两直线平行).
点评: 此题主要考查了角平分线的性质及内错角相等,两直线平行的判定定理.
三.解答题(共16小题)
15.已知:E是AB、CD外一点,∠D=∠B+∠E,求证:AB∥CD.
考点: 三角形的外角性质;平行线的判定.
专题: 证明题.
分析: 欲证AB∥CD,已知∠D=∠B+∠E,且∠BFD=∠B+∠E,即证∴∠D=∠BFD,故可根据内错角相等,两直线平行求证.
解答: 证明:∵∠D=∠B+∠E(已知),∠BFD=∠B+∠E(三角形的一个外角等于与它不相留邻的两个内角的和),∴∠D=∠BFD(等式的性质).∴AB∥CD(内错角相等,两直线平行).
点评: 本题考查的是三角形内角与外角的关系及两直线平行判定定理,比较简单.三角形的一个外角等于和它不相邻的两个内角和.同位角相等、内错角相等、同旁内角互补,两直线平行.
16.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
考点: 平行线的判定;角平分线的定义.
专题: 探究型.
分析: 根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
解答: 解:BE∥DF.理由如下:∵∠A=∠C=90°(已知),∴∠ABC+∠ADC=180°(四边形的内角和等于360°).∵BE平分∠ABC,DF平分∠ADC,∴∠1=∠2=∠ABC,∠3=∠4=∠ADC(角平分线的定义).∴∠1+∠3=(∠ABC+∠ADC)=×180°=90°(等式的性质).又∠1+∠AEB=90°(三角形的内角和等于180°),∴∠3=∠AEB(等量代换).∴BE∥DF(同位角相等,两直线平行).
点评: 此题运用了四边形的内角和定理、角平分线定义、等角的余角相等和平行线的判定,难度中等.
17.已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交CD于E,CF交AB于F,问AE与CF是否平行?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: 想证明AE与CF平行需构造应用平行线判定方法的条件,∠DEA和∠DFC是直线AE与FC被直线CD所截而成的同位角,根据垂直的定义和角平分线的性质可结合图形证得∠DAE=∠DFC,再根据同位角相等,两直线平行可得AE∥CF.
解答: 解:平行.理由如下:∵AD⊥DC,BC⊥AB,∴∠D=∠B=90°.∵∠DAB+∠B+∠BCD+∠D=360°,∴∠DAB+∠BCD=180°.∵AE平分∠BAD,CF平分∠DCB,∴∠DAE+∠DCF=90°.∵∠D+∠DFC+∠DCF=180°,∴∠DFC+∠DCF=90°.∴∠DAE=∠DFC∴AE∥CF.
点评: 正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.本题通过构造同位角相等证明两被截直线平行.
18.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?
考点: 平行线的判定;多边形内角与外角.
专题: 探究型.
分析: 要证BE∥DF,需证∠FDC=∠BEC,由于已知里给出了两条角平分线,ABCD又是四边形,内角和为360°,可得:∠FDC+∠EBC=90°,在△BCE中,∠BEC+∠EBC=90°,等角的余角相等,就可得到∠FDC=∠BEC,即可证.
解答: 解:平行.∵∠A=∠C=90°,四边形ABCD的内角和为360°,∴∠ADC+∠ABC=180°,∵BE平分∠ABC,DF平分∠ADC,∴∠FDC+∠EBC=90°.又∵∠C=90°,∴∠BEC+∠EBC=90°,∴∠FDC=∠BEC,∴BE∥DF.
点评: 本题利用了角平分线性质和判定,四边形的内角和为360°,同角的余角相等.
19.如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由.
考点: 平行线的判定.
专题: 探究型.
分析: 因为DF∥AC,由内错角相等证明∠C=∠FEC,又因为∠C=∠D,则∠D=∠FEC,故CE∥BD.
解答: 解:CE∥BD.理由:∵DF∥AC(已知),∴∠C=∠FEC(两直线平行,内错角相等),又∵∠C=∠D(已知),∴∠D=∠FEC(等量代换),∴CE∥BD(同位角相等,两直线平行).
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题能有效地培养“执果索图”的思维方式与能力.
20.已知:如图,CD⊥AB于D,点E为BC边上的任意一点,EF⊥AB于F,且∠1=∠2,那么BC与DG平行吗?请说明理由.
考点: 平行线的判定.
专题: 探究型.
分析: 要说明BC∥DG,需先确定与两直线都相交的第三线.图中有三条AB、AC、CD,很显然利用DC更为方便,在“三线八角”中,与已知∠1、∠2都相关的角为∠DCB.至此,证题途径已经明朗.
解答: 解:∵CD⊥AB,EF⊥AB,∴CD∥EF;∴∠1=∠BCD(两直线平行,同位角相等);又∵∠1=∠2(已知),∴∠2=∠BCD;∴BC∥DG(内错角相等,两直线平行).
点评: 本题主要考查了平行线的性质和判定.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角的关系.
21.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:因为∠1=∠2,所以 AE ∥ CF ,( 同位角相等,两直线平行 )
所以∠EAC=∠ACG,( 两直线平行,内错角相等 )
因为AB平分∠EAC,CD平分∠ACG,
所以 ∠3 =, ∠4 =,
所以 ∠3 = ∠4 ,
所以AB∥CD( 内错角相等,两直线平行 ).
考点: 平行线的判定.
专题: 推理填空题.
分析: 利用平行线的判定及性质就可求得本题.即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.反之即为性质.
解答: 证明:因为∠1=∠2,所以AE∥CF(同位角相等,两直线平行),所以∠EAC=∠ACG(两直线平行,内错角相等),因为AB平分∠EAC,CD平分∠ACG,所以∠3=,∠4=,所以∠3=∠4,所以AB∥CD(内错角相等,两直线平行).
点评: 此题主要考查了平行线的判定即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.平行线的判定即两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.
22.已知:如图,AB∥CD,∠ABE=∠DCF,请说明∠E=∠F的理由.
考点: 平行线的判定.
专题: 证明题.
分析: 根据两直线平行内错角相等可得,∠ABC=∠BCD结合已知又可知∠EBC=∠FCB,所以BE∥CF(内错角相等,两直线平行)从而证两角相等.
解答: 解:∵AB∥CD(已知),∴∠ABC=∠BCD(两直线平行内错角相等),∵∠ABE=∠DCF(已知),∴∠EBC=∠FCB,∴BE∥CF(内错角相等,两直线平行),∴∠E=∠F(两直线平行内错角相等).
点评: 本题主要利用平行线的性质和判定及图中角的和差关系来证明.
23.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: (1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.
解答: 解:(1)平行,证明:∵∠2+∠CDB=180°,∠1+∠2=180°,∴∠CDB=∠1,∴AE∥FC.(2)平行,证明:∵AE∥FC,∴∠CDA+∠DAE=180°,∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,∴AD∥BC.(3)平分,证明:∵AE∥FC,∴∠EBC=∠BCF,∵AD∥BC,∴∠BCF=∠FDA,∠DBC=∠BDA,又∵DA平分∠BDF,即∠FDA=∠BDA,∴∠EBC=∠DBC,∴BC平分∠DBE.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索图”的思维方式与能力.
24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.
求证:AD∥BC.
考点: 平行线的判定.
专题: 证明题.
分析: 首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.
解答: 证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.
点评: 本题考查角平分线的性质以及平行线的判定定理.
25.如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
考点: 平行线的判定.
专题: 证明题.
分析: 先由已知证明AD∥EF,再证明1∠1=∠4,∠2=∠4,等量代换得出∠1=∠2.
解答: 证明:∵AD⊥BC,EF⊥BC(已知),∴AD∥EF(垂直于同一条直线的两直线平行),∴∠1=∠4(两直线平行,同位角相等),又∵∠3=∠C(已知),∴AC∥DG(同位角相等,两直线平行),∴∠2=∠4(两直线平行,内错角相等),∴∠1=∠2(等量代换).
点评: 此题的关键是理解平行线的性质及判定.①两直线平行,同位角相等.②两直线平行,内错角相等.③同位角相等,两直线平行.④内错角相等,两直线平行.
26.如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
考点: 平行线的判定.
专题: 探究型.
分析: 设AB与DE相交于H,若判断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.
解答: 解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,又∵∠5=∠6,∴∠BAF=∠6,∴AB∥CD,∴∠2=∠EHA,又∵∠1=∠2,即∠1=∠EHA,∴BF∥DE.另解:BF、DE互相平行;理由:如图;∵∠3=∠4,∴BD∥CF,∴∠5=∠BAF,∵∠5=∠6,∴∠BAF=∠6,∵△BFA、△DEC的内角和都是180°∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6∵∠1=∠2;∠BAF=∠6∴∠BFA=∠4(同位角相等,两直线就平行)∴BF∥DE.
点评: 解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.
27.如图,∠1=30°,∠B=60°,AB⊥AC.
①∠DAB+∠B=多少度?
②AD与BC平行吗?AB与CD平行吗?试说明理由.
考点: 平行线的判定.
专题: 探究型.
分析: (1)由已知可求得∠DAB=120°,从而可求得∠DAB+∠B=180°(2)根据同旁内角互补两直线平行可得AD∥BC,∠ACD不能确定从而不能确定AB与CD平行.
解答: 解:①∵AB⊥AC,∴∠BAC=90°,又∠1=30°,∴∠BAD=120°,∵∠B=60°,∴∠DAB+∠B=180°(7分).②答:AD∥BC,AB与CD不一定平行.(3分)理由是:∵∠DAB+∠B=180°∴AD∥BC(4分)∵∠ACD不能确定(5分)∴AB与CD不一定平行.(6分)
点评: 此题主要考查学生对平行线的判定的理解及运用.
28.如图,已知CD⊥AD,DA⊥AB,∠1=∠2.则DF与AE平行吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: DF和AE的截线是AD,欲证FD∥AE,需证∠FDA=∠DAE,由已知条件易得此结论.
解答: 解:FD∥AE.理由如下:∵CD⊥AD,DA⊥AB,∴∠2+∠FDA=90°,∠1+∠DAE=90°,又∠1=∠2,∴∠FDA=∠DAE,∴FD∥AE(内错角相等,两直线平行).
点评: 本题利用了等角的余角相等,还有平行线的判定:内错角相等,两直线平行.
29.已知:如图在四边形ABCD中,∠A=∠D、∠B=∠C,试判断AD与BC的位置关系,并说明理由.
考点: 平行线的判定.
分析: 根据四边形ABCD的内角和是360°,结合已知条件得到∠A+∠B=180°,根据同旁内角互补,两直线平行得AD∥BC.
解答: 解:AD与BC的位置关系是平行.理由:∵四边形ABCD的内角和是360°,∴∠A+∠B+∠C+∠D=360°,∵∠A=∠D,∠B=∠C,∴∠A+∠B+∠B+∠A=360°,∴∠A+∠B=180°,∴AD∥BC(同旁内角互补,两直线平行).
点评: 本题考查四边形的内角和以及利用同旁内角互补,两直线平行进行解答.
30.如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
考点: 平行线的判定.
专题: 探究型.
分析: 本题可通过证直线EF与BD的内错角∠1和∠2相等,来得出EF∥BD的结论.
解答: 解:EF∥BD;理由如下:∵∠AED=60°,EF平分∠AED,∴∠FED=30°,又∵∠FEB=∠2=30°,∴EF∥BD(内错角相等,两直线平行).
点评: 本题主要考查了平行线的判定方法:内错角相等,两直线平行.
PAGE
20
2013.10.12平行线的判定
