2022-2023学年京改版数学九年级上册 19.1二次函数 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年京改版数学九年级上册 19.1二次函数 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 944.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 15:11:33 | ||
图片预览






文档简介
(共16张PPT)
19.1二次函数
1.通过对多个实际问题的分析,让学生感受二次函数作为刻画现实世界有效模型的意义;通过观察和分析,学生归纳出二次函数的概念并能够根据函数特征识别二次函数.
2.学生能对具体情境中的数学信息作出合理的解释,能用二次函数来描述和刻画现实事物间的函数关系.
3.体验数学与日常生活密切相关,让学生认识到许多问题可以用数学方法解决,体验实际问题“数学化”的过程.
教学目标
里约奥运会上,哪位奥运健儿给你留下了深刻的印象?你能猜出下面表情包是谁吗?
你们是根据哪些特征猜出的呢?
情境导入
某种型号的电脑两年前的销售价为6000元,现降价销售,如果每年的平均降价率为x,怎样用x来表示该型号电脑现在的售价y(元)?
想一想:
解:笔记本电脑每次降价后的售价都是降价前的(1-x)倍,我们容易得到售价y与平均降价率x之间有如下的关系:
y = 6000(1-x)2, 0<x<1,
即 y = 6000x2-12000x+6000,0<x<1. ②
②式表示两年后的售价y与平均降价率x之间的关系,而且对于x的每一个取值,y都有唯一确定的值与它对应,即y是x的函数.
y = 6000x2-12000x+6000,0<x<1.
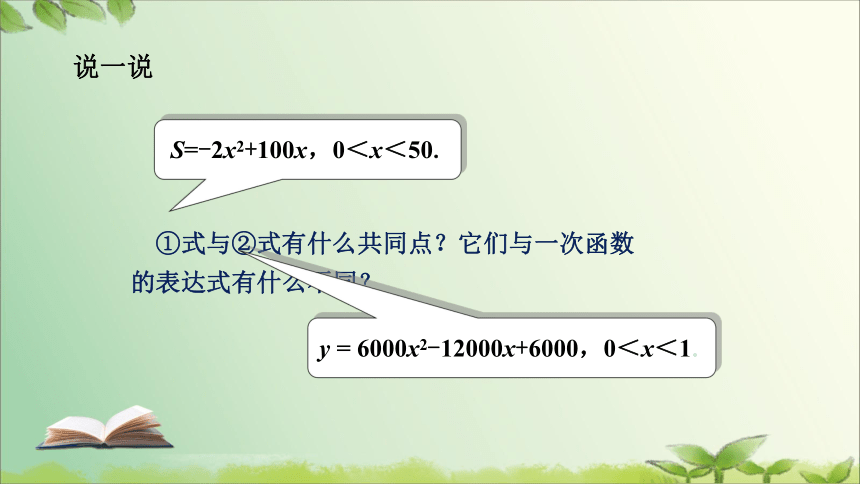
①式与②式有什么共同点?它们与一次函数的表达式有什么不同?
S=-2x2+100x,0<x<50.
y = 6000x2-12000x+6000,0<x<1.
说一说
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项;
如下图,一块矩形木板,长为120cm、宽为80cm, 在木板4个角上各截去边长为x(cm)的正方形,求余下面积S(cm2)与x 之间的函数表达式.
解 木板余下面积S与截去正方形边长x有如下
函数关系:
S =120×80-4×x2 = -4x2 +9600,0<x≤40.
分析 本问题中的数量关系是:
木板余下面积=矩形面积-截去面积.
做一做:
(1)列出下列函数的解析式;
(2)观察所列出的解析式,它们有什么共
同的特点 这些解析式可以用怎样的
式子来概括
(1)圆的面积A是它半径r的函数;
(2)如图,利用成直角的墙角,用20m长的栅栏围成一个矩形的小花园,花园面积S(m2)是它一边长a(m)的函数;
(3)正方形中圆的半径是4cm,阴影面积Q(cm2)是正方形的边长x(cm)的函数;
(4)某种药品现价每盒26元,计划两年内每年的降价率为p,那么,两年后这种药品每盒的价格M(元)是年降价率p的函数.
S
a
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数
其中,ax2叫二次项,a叫做二次项系数
bx叫做一次项, b叫做一次项系数
c叫做常数项
例.已知:如图,一个边长为8cm的正方形,把它的边长延长pcm后得到一个新的正方形,那么,周长增大的部分C(cm)和面积增大的部分Q(cm2)分别是p(cm)的函数.求出这两个函数的解析式,并判断它们的类型,如果是二次函数,写出解析式中a、b、c的值.
8
p
(2)当k取何值时,函数
是①一次函数;②二次函数.
练习:
(1)已知二次函数 ,
求m的值.
圆的半径是1cm,假设半径增加xcm时,圆的面积增加ycm .
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm, ,
2cm时,圆的面积增加多少?
二次函数
定 义
y=ax2+bx+c(a ≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
课堂小结
19.1二次函数
1.通过对多个实际问题的分析,让学生感受二次函数作为刻画现实世界有效模型的意义;通过观察和分析,学生归纳出二次函数的概念并能够根据函数特征识别二次函数.
2.学生能对具体情境中的数学信息作出合理的解释,能用二次函数来描述和刻画现实事物间的函数关系.
3.体验数学与日常生活密切相关,让学生认识到许多问题可以用数学方法解决,体验实际问题“数学化”的过程.
教学目标
里约奥运会上,哪位奥运健儿给你留下了深刻的印象?你能猜出下面表情包是谁吗?
你们是根据哪些特征猜出的呢?
情境导入
某种型号的电脑两年前的销售价为6000元,现降价销售,如果每年的平均降价率为x,怎样用x来表示该型号电脑现在的售价y(元)?
想一想:
解:笔记本电脑每次降价后的售价都是降价前的(1-x)倍,我们容易得到售价y与平均降价率x之间有如下的关系:
y = 6000(1-x)2, 0<x<1,
即 y = 6000x2-12000x+6000,0<x<1. ②
②式表示两年后的售价y与平均降价率x之间的关系,而且对于x的每一个取值,y都有唯一确定的值与它对应,即y是x的函数.
y = 6000x2-12000x+6000,0<x<1.
①式与②式有什么共同点?它们与一次函数的表达式有什么不同?
S=-2x2+100x,0<x<50.
y = 6000x2-12000x+6000,0<x<1.
说一说
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项;
如下图,一块矩形木板,长为120cm、宽为80cm, 在木板4个角上各截去边长为x(cm)的正方形,求余下面积S(cm2)与x 之间的函数表达式.
解 木板余下面积S与截去正方形边长x有如下
函数关系:
S =120×80-4×x2 = -4x2 +9600,0<x≤40.
分析 本问题中的数量关系是:
木板余下面积=矩形面积-截去面积.
做一做:
(1)列出下列函数的解析式;
(2)观察所列出的解析式,它们有什么共
同的特点 这些解析式可以用怎样的
式子来概括
(1)圆的面积A是它半径r的函数;
(2)如图,利用成直角的墙角,用20m长的栅栏围成一个矩形的小花园,花园面积S(m2)是它一边长a(m)的函数;
(3)正方形中圆的半径是4cm,阴影面积Q(cm2)是正方形的边长x(cm)的函数;
(4)某种药品现价每盒26元,计划两年内每年的降价率为p,那么,两年后这种药品每盒的价格M(元)是年降价率p的函数.
S
a
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数
其中,ax2叫二次项,a叫做二次项系数
bx叫做一次项, b叫做一次项系数
c叫做常数项
例.已知:如图,一个边长为8cm的正方形,把它的边长延长pcm后得到一个新的正方形,那么,周长增大的部分C(cm)和面积增大的部分Q(cm2)分别是p(cm)的函数.求出这两个函数的解析式,并判断它们的类型,如果是二次函数,写出解析式中a、b、c的值.
8
p
(2)当k取何值时,函数
是①一次函数;②二次函数.
练习:
(1)已知二次函数 ,
求m的值.
圆的半径是1cm,假设半径增加xcm时,圆的面积增加ycm .
(1)写出y与x之间的函数关系表达式;
(2)当圆的半径分别增加1cm, ,
2cm时,圆的面积增加多少?
二次函数
定 义
y=ax2+bx+c(a ≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
课堂小结
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
