19.6反比例函数的图像、性质和应用 课件(共18张PPT)
文档属性
| 名称 | 19.6反比例函数的图像、性质和应用 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 11:38:27 | ||
图片预览






文档简介
(共18张PPT)
19.6反比例函数的图像、性质和应用
复习回顾
1.反比例函数的定义:
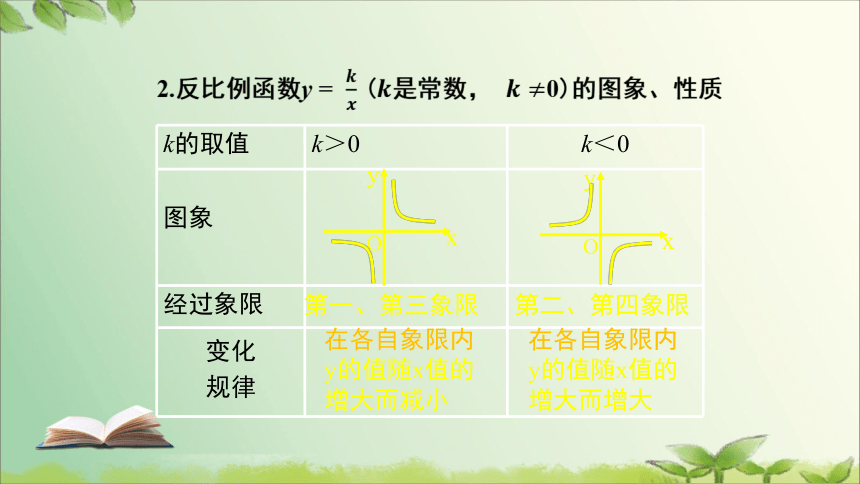
k的取值 k>0 k<0
图象
经过象限
变化
规律
x
y
O
第一、第三象限
在各自象限内
y的值随x值的增大而减小
第二、第四象限
在各自象限内
y的值随x值的增大而增大
x
y
O
问题牵引,导入新课。
1、反比例函数的一般形式为 ,
特殊要求 ,反比例函数还可以写成
形式。
2、一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式。
y是x的反比例函数
x
y
6
活动、挑战“记忆”
描点并连线:
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
… 1 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 -1 …
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
画法
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
列表
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
例 1
x
y =
x
6
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
※(1)列表取值时,x≠0,因为x=0函数无意义,
为了使描出的点具有代表性,可以“0”为中心,向两
边对称式取值,即正、负数各一半,且互为相反数,
这样也便于求y值。
(2)由于函数图象的特征还不清楚,所以要尽量多取
一些数值,多描一些点,这样便于连线,使画出的图象
更精确。
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
提醒学生:由于x≠0,
k≠0,所以y≠0,函数图象永
远不会与x轴、y轴相交,只是
无限靠近两坐标轴 。
你能试着说说反比例函数 的共同特征吗?
反比例函数 的图象
当k>0时,在每一象限内,y的值随x值的增大而 ;
当k<0时,在每一象限内,y的值随x值的增大而 。
减小
增大
小结
例:函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1,y2,y3的
大小关系是_______________.
y3< y1< y2
想一想做一做
例:如图,正比例函数 与反比例函数
的图象交于点A(2,3).
(1)求k、m的值;
(2)写出正比例函数值大于反比例函数值时自变
量x的取值范围.
解:(1)将A(2,3)分别代入 和
中可得: 和
解方程得: 、 m =6.
(2)由图象可知,正比例函数值大于反比例函数值时:x>2.
二四象限
一三象限
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
y随x的增大而增大
一三象限
在每个象限, y随x的增大而减小
二四象限
y随x的增大而减小
在每个象限, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
用对比的方法去记忆效果如何?
A
D
B
M
C
N
3
y
x
拓展 如图,B,C和D三点是∠MAN的边AM和AN上的三个动点,且使∠BDC和∠BCA保持相等,BC = 3.如果AB = y,BD = x, 那么y是x的函数吗?如果是,求出它的表达式.
A
D
B
M
C
N
3
y
x
拓展 如图,B,C和D三点是∠MAN的边AM和AN上的三个动点,且使∠BDC和∠BCA保持相等,BC = 3.如果AB = y,BD = x, 那么y是x的函数吗?如果是,求出它的表达式.
A
D
B
M
C
N
3
y
x
∴△ ABC∽△ CBD.
课堂小结
反比例函数的图象与性质
k>0 k<0
图象
经过象限 第一、三象限 第二、四象限
变化规律 在各自象限内,y的值随x值的增大而减小. 在各自象限内,y的值随x值的增大而增大.
y
x
O
y
x
O
反比例函数图象
经过的象限、变化规律
性质
课堂小结
19.6反比例函数的图像、性质和应用
复习回顾
1.反比例函数的定义:
k的取值 k>0 k<0
图象
经过象限
变化
规律
x
y
O
第一、第三象限
在各自象限内
y的值随x值的增大而减小
第二、第四象限
在各自象限内
y的值随x值的增大而增大
x
y
O
问题牵引,导入新课。
1、反比例函数的一般形式为 ,
特殊要求 ,反比例函数还可以写成
形式。
2、一个矩形的面积为6,相邻两边长分别为x和y,
那么y是x的什么函数?写出y与x的函数关系式。
y是x的反比例函数
x
y
6
活动、挑战“记忆”
描点并连线:
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
… 1 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 -1 …
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
画法
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
列表
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
例 1
x
y =
x
6
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
※(1)列表取值时,x≠0,因为x=0函数无意义,
为了使描出的点具有代表性,可以“0”为中心,向两
边对称式取值,即正、负数各一半,且互为相反数,
这样也便于求y值。
(2)由于函数图象的特征还不清楚,所以要尽量多取
一些数值,多描一些点,这样便于连线,使画出的图象
更精确。
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =-
x
6
提醒学生:由于x≠0,
k≠0,所以y≠0,函数图象永
远不会与x轴、y轴相交,只是
无限靠近两坐标轴 。
你能试着说说反比例函数 的共同特征吗?
反比例函数 的图象
当k>0时,在每一象限内,y的值随x值的增大而 ;
当k<0时,在每一象限内,y的值随x值的增大而 。
减小
增大
小结
例:函数 的图象上有三点
(-3,y1), (-1,y2), (2,y3),则函数值y1,y2,y3的
大小关系是_______________.
y3< y1< y2
想一想做一做
例:如图,正比例函数 与反比例函数
的图象交于点A(2,3).
(1)求k、m的值;
(2)写出正比例函数值大于反比例函数值时自变
量x的取值范围.
解:(1)将A(2,3)分别代入 和
中可得: 和
解方程得: 、 m =6.
(2)由图象可知,正比例函数值大于反比例函数值时:x>2.
二四象限
一三象限
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
y随x的增大而增大
一三象限
在每个象限, y随x的增大而减小
二四象限
y随x的增大而减小
在每个象限, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
用对比的方法去记忆效果如何?
A
D
B
M
C
N
3
y
x
拓展 如图,B,C和D三点是∠MAN的边AM和AN上的三个动点,且使∠BDC和∠BCA保持相等,BC = 3.如果AB = y,BD = x, 那么y是x的函数吗?如果是,求出它的表达式.
A
D
B
M
C
N
3
y
x
拓展 如图,B,C和D三点是∠MAN的边AM和AN上的三个动点,且使∠BDC和∠BCA保持相等,BC = 3.如果AB = y,BD = x, 那么y是x的函数吗?如果是,求出它的表达式.
A
D
B
M
C
N
3
y
x
∴△ ABC∽△ CBD.
课堂小结
反比例函数的图象与性质
k>0 k<0
图象
经过象限 第一、三象限 第二、四象限
变化规律 在各自象限内,y的值随x值的增大而减小. 在各自象限内,y的值随x值的增大而增大.
y
x
O
y
x
O
反比例函数图象
经过的象限、变化规律
性质
课堂小结
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
