2.3 用计算器求锐角三角比 课件(共16张PPT)
文档属性
| 名称 | 2.3 用计算器求锐角三角比 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.3 用计算器求锐角三角比
温故知新
特殊角的三角比.
角α
三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
问题:
(1)当锐角α的度数逐渐增大时,sinα,cosα,tanα
值的增减性是什么?
(2)锐角三角比sinα,cosα,tanα的取值范围是什么?
tan
第一步:按计算器 键,
求 tan30°36'.
第二步:输入角度值30,分值36 (可以使用 键),
°' ″
屏幕显示答案:0.591 398 351;
第一种方法:
第二种方法:
tan
第一步:按计算器 键,
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
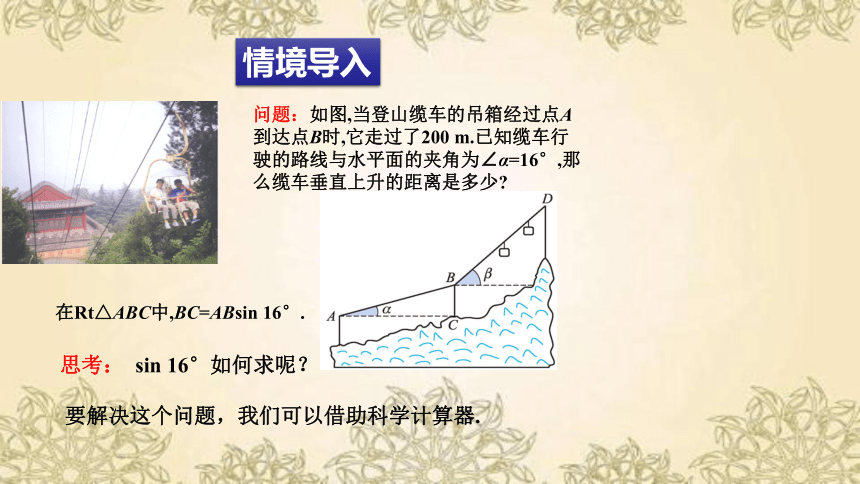
问题:如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少
在Rt△ABC中,BC=ABsin 16°. °..
情境导入
思考: sin 16°如何求呢?
要解决这个问题,我们可以借助科学计算器.
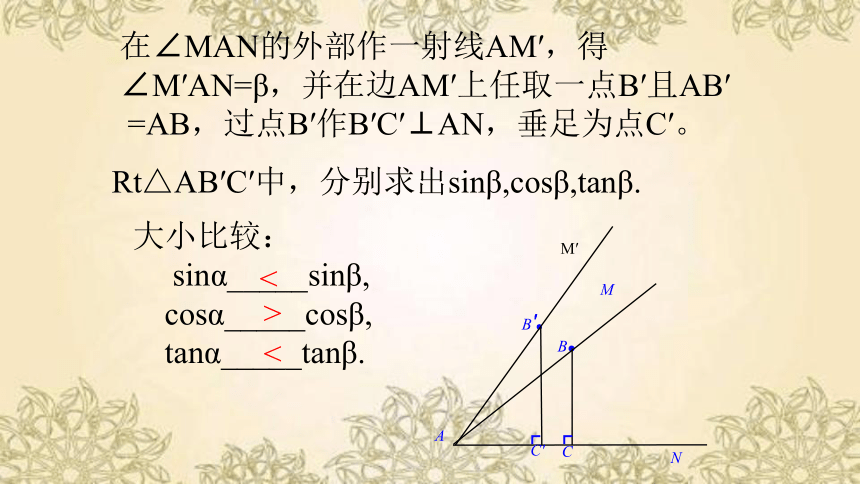
在∠MAN的外部作一射线AM′,得∠M′AN=β,并在边AM′上任取一点B′且AB′
=AB,过点B′作B′C′⊥AN,垂足为点C′。
Rt△AB′C′中,分别求出sinβ,cosβ,tanβ.
B●
B′●
A
M
N
C
┏
C′
┏
M′
大小比较:
sinα_____sinβ,
cosα_____cosβ,
tanα_____tanβ.
<
>
<
例:已知sinA=0.501 8;用计算器求锐角A可以按照下面方法操作:
还以以利用 键,进一步得到
∠A=30°07'08.97 "
第一步:按计算器 键,
2nd F
sin
第二步:然后输入函数值0. 501 8
屏幕显示答案: 30.119 158 67° (按实际需要进行精确)
第一种方法:
°'″
2nd F
学习新知
用计算器求三角比值
1.求sin 18°.
第二步:输入角度值18,
屏幕显示结果sin 18°=0.309 016 994
(也有的计算器是先输入角度再按函数名称键.)
第一步:按计算器 键,
锐角α的有关规律
1、三角比的增减性:
正弦:锐角α的正弦值随着度数的增大
而增大;
余弦:锐角α的余弦值随着度数的增大
而减小;
正切:锐角α的正切值随着度数的增大
而增大。
2、三角比的取值范围:
当0°<α<90°时,
0o
用计算器求下列锐角三角函数值;
(1) sin20°= , cos70°= ;
(2)tan3°8 ' = ,tan80°25'43″= .
sin35°= ,cos55°= ;
sin15°32 ' = ,cos74°28 ' = .
分析第1(1)题的结果,你能得出什么猜想,你能说明你的猜想吗?
0.342
0.342
0.574
0.268
0.574
0.268
5.930
0.055
例1 用计算器求下列各式的值:
(1)sin 38°17′18″ ; (2)cos 42.3°;
(3)tan 62°19′41″.
典例精析
知识探索
A
C
B
┏
在Rt△ABC中,分别求出sinA,cosA,tanA,
sinB,cosB,tanB.
大小比较:
(1) sinA__ cosB, sinB__ cosA.
=
=
=
=
=1
=1
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
利用计算器由三角比的值求角度
如果已知锐角三角比值,也可以使用计算器求出相应的锐角.
随堂练习
1、大小比较:sin37°____cos42°
2、下列各式的值可能为 是( )
=sin48°
<
D
课堂小结
本节课到此结束,相信大家已经初步掌握了许多的新知识,要通过课后习题进行复习巩固
2.3 用计算器求锐角三角比
温故知新
特殊角的三角比.
角α
三角比 30° 45° 60°
sin α
cosα
tanα
1
2
1
2
2
2
3
3
2
1
2
3
2
2
3
3
问题:
(1)当锐角α的度数逐渐增大时,sinα,cosα,tanα
值的增减性是什么?
(2)锐角三角比sinα,cosα,tanα的取值范围是什么?
tan
第一步:按计算器 键,
求 tan30°36'.
第二步:输入角度值30,分值36 (可以使用 键),
°' ″
屏幕显示答案:0.591 398 351;
第一种方法:
第二种方法:
tan
第一步:按计算器 键,
第二步:输入角度值30.6 (因为30°36'=30.6°)
屏幕显示答案:0.591 398 351.
问题:如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少
在Rt△ABC中,BC=ABsin 16°. °..
情境导入
思考: sin 16°如何求呢?
要解决这个问题,我们可以借助科学计算器.
在∠MAN的外部作一射线AM′,得∠M′AN=β,并在边AM′上任取一点B′且AB′
=AB,过点B′作B′C′⊥AN,垂足为点C′。
Rt△AB′C′中,分别求出sinβ,cosβ,tanβ.
B●
B′●
A
M
N
C
┏
C′
┏
M′
大小比较:
sinα_____sinβ,
cosα_____cosβ,
tanα_____tanβ.
<
>
<
例:已知sinA=0.501 8;用计算器求锐角A可以按照下面方法操作:
还以以利用 键,进一步得到
∠A=30°07'08.97 "
第一步:按计算器 键,
2nd F
sin
第二步:然后输入函数值0. 501 8
屏幕显示答案: 30.119 158 67° (按实际需要进行精确)
第一种方法:
°'″
2nd F
学习新知
用计算器求三角比值
1.求sin 18°.
第二步:输入角度值18,
屏幕显示结果sin 18°=0.309 016 994
(也有的计算器是先输入角度再按函数名称键.)
第一步:按计算器 键,
锐角α的有关规律
1、三角比的增减性:
正弦:锐角α的正弦值随着度数的增大
而增大;
余弦:锐角α的余弦值随着度数的增大
而减小;
正切:锐角α的正切值随着度数的增大
而增大。
2、三角比的取值范围:
当0°<α<90°时,
0
用计算器求下列锐角三角函数值;
(1) sin20°= , cos70°= ;
(2)tan3°8 ' = ,tan80°25'43″= .
sin35°= ,cos55°= ;
sin15°32 ' = ,cos74°28 ' = .
分析第1(1)题的结果,你能得出什么猜想,你能说明你的猜想吗?
0.342
0.342
0.574
0.268
0.574
0.268
5.930
0.055
例1 用计算器求下列各式的值:
(1)sin 38°17′18″ ; (2)cos 42.3°;
(3)tan 62°19′41″.
典例精析
知识探索
A
C
B
┏
在Rt△ABC中,分别求出sinA,cosA,tanA,
sinB,cosB,tanB.
大小比较:
(1) sinA__ cosB, sinB__ cosA.
=
=
=
=
=1
=1
1. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.
∠B=38°8″
∠A=38°51′57″
∠A=51°18′11″
∠B=80°27′2″
∠A=78°19′58″
∠B=41°23′58″
利用计算器由三角比的值求角度
如果已知锐角三角比值,也可以使用计算器求出相应的锐角.
随堂练习
1、大小比较:sin37°____cos42°
2、下列各式的值可能为 是( )
=sin48°
<
D
课堂小结
本节课到此结束,相信大家已经初步掌握了许多的新知识,要通过课后习题进行复习巩固
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
