2.4 解直角三角形 课件(共15张PPT)
文档属性
| 名称 | 2.4 解直角三角形 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 443.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 21:26:12 | ||
图片预览



文档简介
(共15张PPT)
2.4 解直角三角形
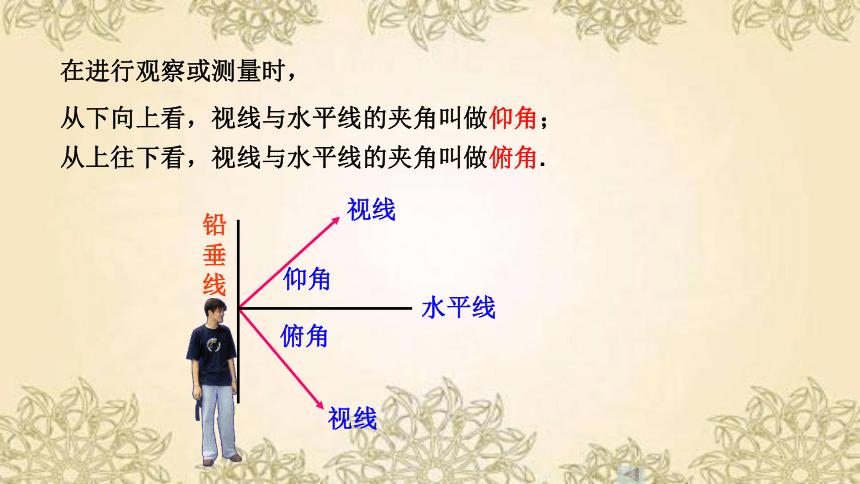
铅垂线
水平线
视线
视线
仰角
俯角
在进行观察或测量时,
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
知 识回 顾
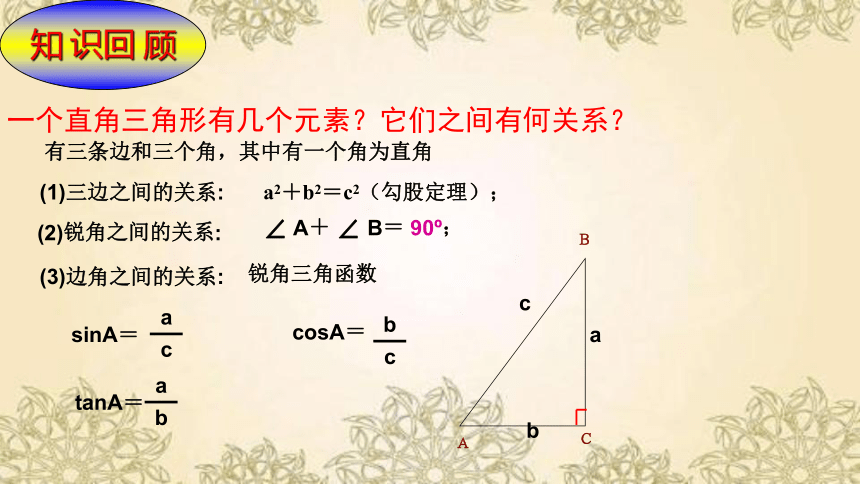
一个直角三角形有几个元素?它们之间有何关系?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
有三条边和三个角,其中有一个角为直角
b
c
a
b
锐角三角函数
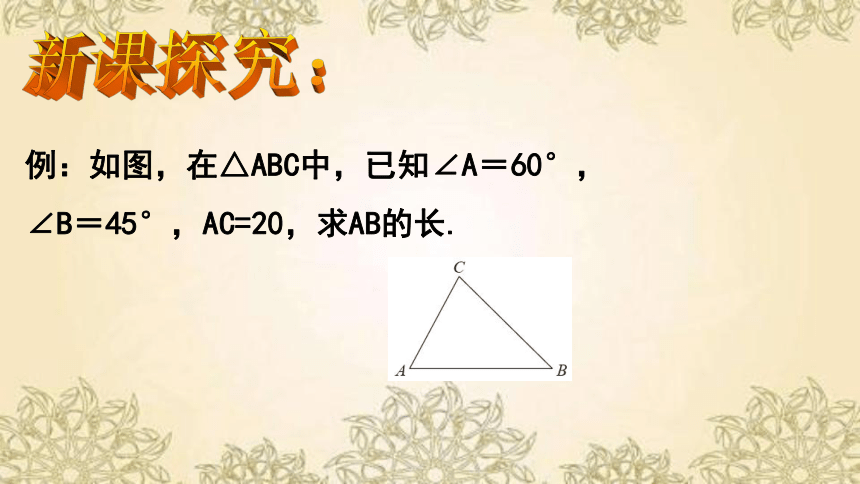
例:如图,在△ABC中,已知∠A=60°,
∠B=45°,AC=20,求AB的长.
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
通过作垂线(高),将斜三角形分割成两个直角三角
形,然后利用解直角三角形来解决边或角的问题,这种
“化斜为直”的思想很常见.在作垂线时,要结合已知
条件,充分利用已知条件,如本题若过B点作AC的垂线,
则∠B的正弦值就无法利用.
A
B
a
b
c
C
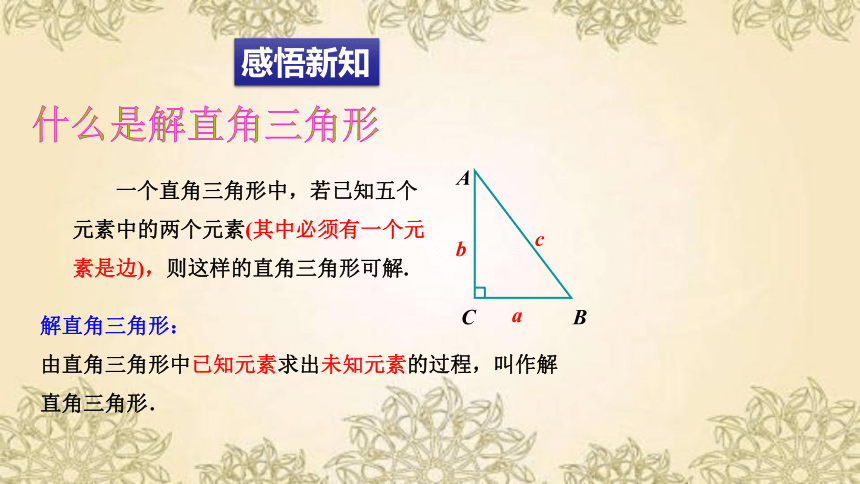
解直角三角形:
由直角三角形中已知元素求出未知元素的过程,叫作解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
感悟新知
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
如图,为了测量电线杆的高度AB,在离电线杆30米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.
1.20
30
=300
1、如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )米.
A.25 B. C. D.
B
C
A
D
l
B
在Rt△ABC中,如果已知其中两边的长,你能求出
这个三角形的其他元 素吗?
类型1 已知两边解直角三角形
基础练习
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
D
在山顶上D处有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。
A
B
C
D
α
β
30米
30°
45°
x
x
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过 ,求 ∠A
已知∠A,a. 则b= c= a
3.已知∠A,b. 则a= 的
2. 已知∠A,c. 则a= b= a
提高练习
5.已知b,c.则通过 ,求 ∠A
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
2.4 解直角三角形
铅垂线
水平线
视线
视线
仰角
俯角
在进行观察或测量时,
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
知 识回 顾
一个直角三角形有几个元素?它们之间有何关系?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
有三条边和三个角,其中有一个角为直角
b
c
a
b
锐角三角函数
例:如图,在△ABC中,已知∠A=60°,
∠B=45°,AC=20,求AB的长.
应用勾股定理求斜边,
应用角的正切值求出
一锐角,再利用直角
三角形的两锐角互余,求出另一锐角.一般不用正弦或余弦值求锐角,因为斜边是一个中间量,如果是近似值,会影响结果的精确度.
已知斜边和直角边:先利用勾股定理求出另一直角边,再求一锐角的正弦和余弦值,即可求出一锐角,再利用直角三角形的两锐角互余,求出另一锐角.
已知两直角边:
已知斜边和直角边:
通过作垂线(高),将斜三角形分割成两个直角三角
形,然后利用解直角三角形来解决边或角的问题,这种
“化斜为直”的思想很常见.在作垂线时,要结合已知
条件,充分利用已知条件,如本题若过B点作AC的垂线,
则∠B的正弦值就无法利用.
A
B
a
b
c
C
解直角三角形:
由直角三角形中已知元素求出未知元素的过程,叫作解直角三角形.
一个直角三角形中,若已知五个元素中的两个元素(其中必须有一个元素是边),则这样的直角三角形可解.
感悟新知
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
你能求出这三个角的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
如图,为了测量电线杆的高度AB,在离电线杆30米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=30°,求电线杆AB的高.
1.20
30
=300
1、如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )米.
A.25 B. C. D.
B
C
A
D
l
B
在Rt△ABC中,如果已知其中两边的长,你能求出
这个三角形的其他元 素吗?
类型1 已知两边解直角三角形
基础练习
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
D
在山顶上D处有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。
A
B
C
D
α
β
30米
30°
45°
x
x
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过 ,求 ∠A
已知∠A,a. 则b= c= a
3.已知∠A,b. 则a= 的
2. 已知∠A,c. 则a= b= a
提高练习
5.已知b,c.则通过 ,求 ∠A
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
