2.5.2 解直角三角形的应用 2 课件(共16张PPT)
文档属性
| 名称 | 2.5.2 解直角三角形的应用 2 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 982.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 21:27:35 | ||
图片预览





文档简介
(共16张PPT)
2.5.2 解直角三角形的应用 2
如图,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c .
(1)直角三角形的三边之间有什么关系?
(2)直角三角形的锐角之间有什么关系?
(3)直角三角形的边和锐角之间有什么关系?
a2+b2=c2(勾股定理)
∠A+∠B=90°.
α
h
1、坡角
与 的夹角叫做坡角,记作α 。
2、坡度(或坡比)
3、坡度与坡角的关系
坡面
水平面
坡度越大,坡角就越 ,坡面就越 .
垂直高度
水平宽度
如图所示,坡面的 (h)和 (l)
的比叫做坡面的坡度(或坡比),记作 i,即
坡面
水平面
垂直高度
水平宽度
大
陡
如图, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?右边的路BD陡些.如何用数量来刻画哪条路陡呢?
右边的BD陡些.
如何用数量来刻画哪条陡路呢?
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OE
A
B
C
D
OF
OG
OH
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方向角
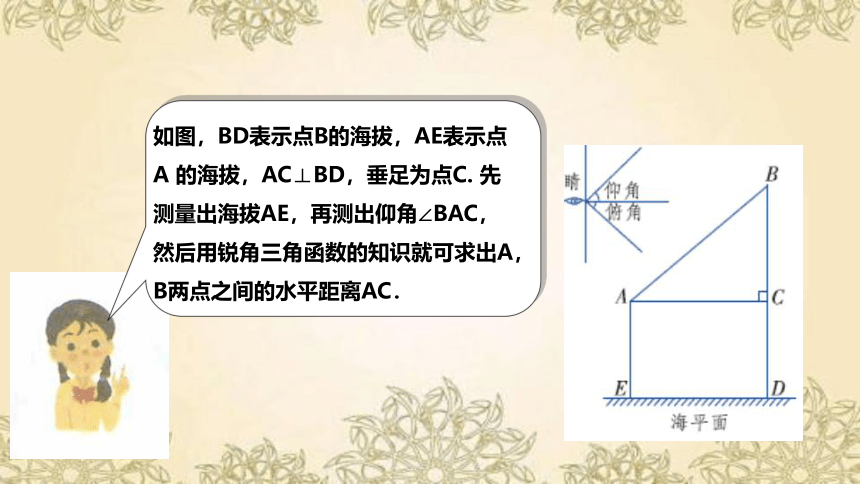
如图,BD表示点B的海拔,AE表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
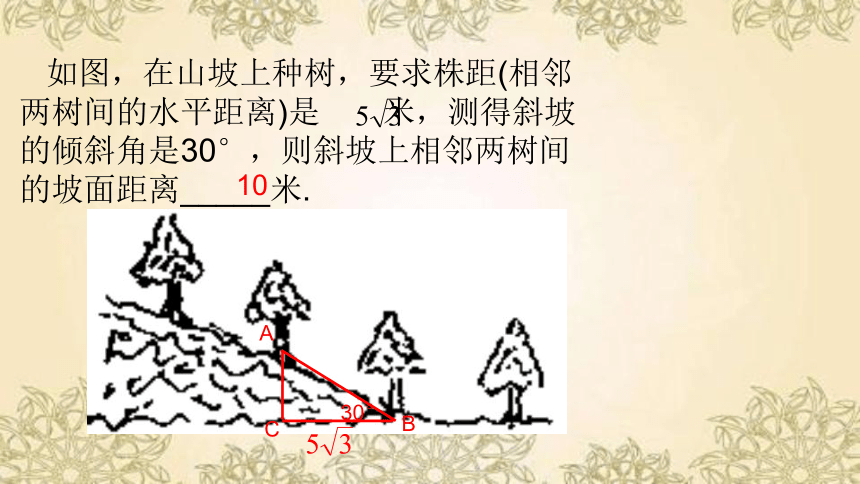
如图,在山坡上种树,要求株距(相邻两树间的水平距离)是 米,测得斜坡的倾斜角是30°,则斜坡上相邻两树间的坡面距离_____米.
10
30°
A
B
C
B
C
A
北
30°
60°
分析:
只需要计算垂线段CD的长度即可.
CD即渔船与小岛的最近距离,
当CD≥10时,没有危险;
当CD<10时,有危险.
D
例.如图,在离上海东方明珠塔底部1000 m 的A 处,用仪器测得塔顶的仰角∠BAC 为25°,仪器距地面高AE为1.7 m. 求上海东方明珠塔的高度BD(结果精确到1 m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
用三角函数求边长时的注意事项
讲解知识
用解直角三角形知识解决此类问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
1.如图,坡面的铅直高度h和水平宽度l的比叫作坡面的_______,记作i,即i=_____(坡度通常写成_______的形式).坡面与________的夹角叫作坡角,记作α.显然坡度等于坡角的________,即i=____=_________.坡度越________,山坡越陡.
课堂练习
坡度
1:m
水平面
tanα
正切
大
2.一水坝的横断面是梯形ABCD,迎水坡CD的坡角a=30°,背水坡AB的坡度i=1∶1, 坝顶宽BC=2.5m,坝高4.5m;
在上述问题中,为了提高堤坝的抗洪能力,防汛指挥部决定加固堤坝,要求坝顶BC加宽0.5m,背水坡AB的坡度改为1∶1.4,已知堤坝的总长为5km,
求:(1)加宽部分横截面的面积。
(2)完成该项工程需要多少立方米的土?
A
B
C
D
1∶1
1∶1.4
F
N
0.5
E
∟
M
∟
课堂练习
C
课堂小结
今天这节课就到此结束,同学们如果还有其他的问题,请同学们在课下去问老师和其他同学们进行学习,以便可以将这节课的内容融会贯通。
2.5.2 解直角三角形的应用 2
如图,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c .
(1)直角三角形的三边之间有什么关系?
(2)直角三角形的锐角之间有什么关系?
(3)直角三角形的边和锐角之间有什么关系?
a2+b2=c2(勾股定理)
∠A+∠B=90°.
α
h
1、坡角
与 的夹角叫做坡角,记作α 。
2、坡度(或坡比)
3、坡度与坡角的关系
坡面
水平面
坡度越大,坡角就越 ,坡面就越 .
垂直高度
水平宽度
如图所示,坡面的 (h)和 (l)
的比叫做坡面的坡度(或坡比),记作 i,即
坡面
水平面
垂直高度
水平宽度
大
陡
如图, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?右边的路BD陡些.如何用数量来刻画哪条路陡呢?
右边的BD陡些.
如何用数量来刻画哪条陡路呢?
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OE
A
B
C
D
OF
OG
OH
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
认识方向角
如图,BD表示点B的海拔,AE表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
如图,在山坡上种树,要求株距(相邻两树间的水平距离)是 米,测得斜坡的倾斜角是30°,则斜坡上相邻两树间的坡面距离_____米.
10
30°
A
B
C
B
C
A
北
30°
60°
分析:
只需要计算垂线段CD的长度即可.
CD即渔船与小岛的最近距离,
当CD≥10时,没有危险;
当CD<10时,有危险.
D
例.如图,在离上海东方明珠塔底部1000 m 的A 处,用仪器测得塔顶的仰角∠BAC 为25°,仪器距地面高AE为1.7 m. 求上海东方明珠塔的高度BD(结果精确到1 m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
用三角函数求边长时的注意事项
讲解知识
用解直角三角形知识解决此类问题的一般步骤:
(1)通过读题把已知转化为数学图形;
(2)找出直角三角形和已知、未知元素;
(3)选择合适的锐角三角函数求未知数;
(4)解题.
1.如图,坡面的铅直高度h和水平宽度l的比叫作坡面的_______,记作i,即i=_____(坡度通常写成_______的形式).坡面与________的夹角叫作坡角,记作α.显然坡度等于坡角的________,即i=____=_________.坡度越________,山坡越陡.
课堂练习
坡度
1:m
水平面
tanα
正切
大
2.一水坝的横断面是梯形ABCD,迎水坡CD的坡角a=30°,背水坡AB的坡度i=1∶1, 坝顶宽BC=2.5m,坝高4.5m;
在上述问题中,为了提高堤坝的抗洪能力,防汛指挥部决定加固堤坝,要求坝顶BC加宽0.5m,背水坡AB的坡度改为1∶1.4,已知堤坝的总长为5km,
求:(1)加宽部分横截面的面积。
(2)完成该项工程需要多少立方米的土?
A
B
C
D
1∶1
1∶1.4
F
N
0.5
E
∟
M
∟
课堂练习
C
课堂小结
今天这节课就到此结束,同学们如果还有其他的问题,请同学们在课下去问老师和其他同学们进行学习,以便可以将这节课的内容融会贯通。
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
