2.5.3 解直角三角形的应用3 课件(共15张PPT)
文档属性
| 名称 | 2.5.3 解直角三角形的应用3 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 637.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 21:28:57 | ||
图片预览






文档简介
(共15张PPT)
2.5.3 解直角三角形的应用 3
学习目标
1、了解方位角、坡度、坡角等概念,学会构造直角三角形后解直角三角形进而解决实际问题。
2、逐步培养学生分析问题、解决问题的能力。
3、巩固用三角函数有关知识解决问题,学会解决方位角、坡度、坡角问题。
学习重点
构造直角三角形解决实际问题
学习难点
方位角的画法,坡度的概念、构造直角形解决实际问题
运用三角函数解决实际应用问题
答题思路
知识点框架
仰角和俯角
如图所示,当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角.
铅垂线
仰角
俯角
视线
水平线
视线
在日常生活中,我们经常会碰到一些与直角
三角形有关的实际问题.对于这些问题,我们可以
用所学的解直角三角形的知识来加以解决.
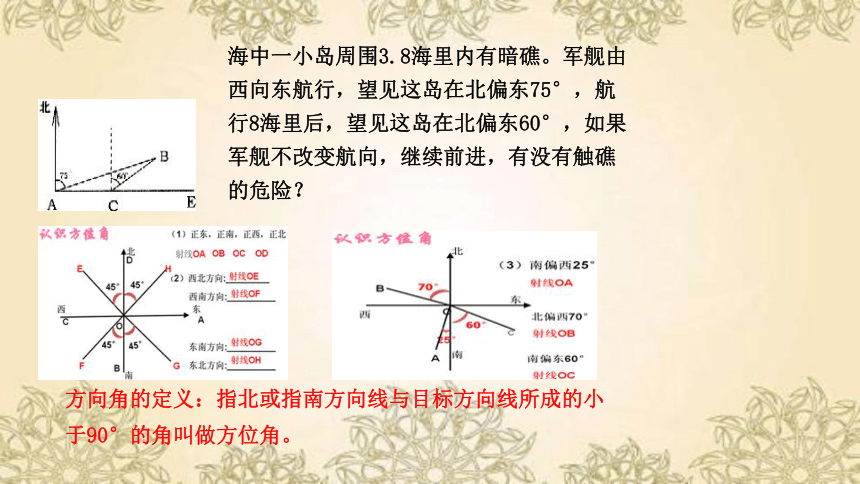
海中一小岛周围3.8海里内有暗礁。军舰由西向东航行,望见这岛在北偏东75°,航行8海里后,望见这岛在北偏东60°,如果军舰不改变航向,继续前进,有没有触礁的危险?
方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
如图, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?
在上图 中,∠BAC 叫作坡角.坡角:坡面与地平面的夹角α叫坡角.
右边的路BD陡些.如何用数量来刻画哪条路陡呢?
坡度(坡比): 如图,坡面的高度h和水平距离l的比叫坡度(或坡比),用字母i表示, 即
(坡度通常写成1 ∶ m的形式)
坡度越大,山坡越陡.
例题探究
例 如图所示, 在离上海东方明珠塔底部1 000 m 的A 处, 用仪器测得塔顶的仰角∠BAC 为25°, 仪器距地面高AE 为1.7 m. 求上海东方明珠塔的高度BD(结果精确到1 m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
解:如图,在Rt△ABC中,∠BAC =25°,AC =100m,
因此
答:上海东方明珠塔的高度BD为468 m.
从而
(m).
因此,上海东方明珠塔的高度
(m).
如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港沿北偏东60°的方向以40海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行_ _海里.
(2014·上海)已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为_ _米.
某水库大坝某段的横断面是等腰梯形,坝顶宽6米,坝底宽126米,斜坡的坡比为1∶ 则此处大坝的坡角和高分别是_ 和 _.
如图所示,一艘轮船以20海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/小时的速度由南向北移动,距台风中心20 海里的圆形区域(包括边界)都属台风区。当轮船到A处时,测得台风中心移到 位于点A正南方向B处,且AB = 100海里。
(1)若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由。
(2)现轮船自A处立即提高船速,向位于东偏北30°方向,相距60海里的D港驶去,为使台风到来之前,到达D港,问船速至少应提高多少?
A
B
D
·
·
·
G
E
F
C
能力提升
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB高为1.5米,求拉线CE的长.(结果保留根号)
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
2.5.3 解直角三角形的应用 3
学习目标
1、了解方位角、坡度、坡角等概念,学会构造直角三角形后解直角三角形进而解决实际问题。
2、逐步培养学生分析问题、解决问题的能力。
3、巩固用三角函数有关知识解决问题,学会解决方位角、坡度、坡角问题。
学习重点
构造直角三角形解决实际问题
学习难点
方位角的画法,坡度的概念、构造直角形解决实际问题
运用三角函数解决实际应用问题
答题思路
知识点框架
仰角和俯角
如图所示,当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角.
铅垂线
仰角
俯角
视线
水平线
视线
在日常生活中,我们经常会碰到一些与直角
三角形有关的实际问题.对于这些问题,我们可以
用所学的解直角三角形的知识来加以解决.
海中一小岛周围3.8海里内有暗礁。军舰由西向东航行,望见这岛在北偏东75°,航行8海里后,望见这岛在北偏东60°,如果军舰不改变航向,继续前进,有没有触礁的危险?
方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角叫做方位角。
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
如图, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?
在上图 中,∠BAC 叫作坡角.坡角:坡面与地平面的夹角α叫坡角.
右边的路BD陡些.如何用数量来刻画哪条路陡呢?
坡度(坡比): 如图,坡面的高度h和水平距离l的比叫坡度(或坡比),用字母i表示, 即
(坡度通常写成1 ∶ m的形式)
坡度越大,山坡越陡.
例题探究
例 如图所示, 在离上海东方明珠塔底部1 000 m 的A 处, 用仪器测得塔顶的仰角∠BAC 为25°, 仪器距地面高AE 为1.7 m. 求上海东方明珠塔的高度BD(结果精确到1 m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
解:如图,在Rt△ABC中,∠BAC =25°,AC =100m,
因此
答:上海东方明珠塔的高度BD为468 m.
从而
(m).
因此,上海东方明珠塔的高度
(m).
如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港沿北偏东60°的方向以40海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行_ _海里.
(2014·上海)已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为_ _米.
某水库大坝某段的横断面是等腰梯形,坝顶宽6米,坝底宽126米,斜坡的坡比为1∶ 则此处大坝的坡角和高分别是_ 和 _.
如图所示,一艘轮船以20海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/小时的速度由南向北移动,距台风中心20 海里的圆形区域(包括边界)都属台风区。当轮船到A处时,测得台风中心移到 位于点A正南方向B处,且AB = 100海里。
(1)若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由。
(2)现轮船自A处立即提高船速,向位于东偏北30°方向,相距60海里的D港驶去,为使台风到来之前,到达D港,问船速至少应提高多少?
A
B
D
·
·
·
G
E
F
C
能力提升
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪AB高为1.5米,求拉线CE的长.(结果保留根号)
课堂小结
今天的课到此结束。如果你有任何问题,你可以问老师。我相信每个人都能学会这节课的内容,对今后的学习会有很大的帮助
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
