22.2 二次函数与一元二次方程 课件(共29张PPT)
文档属性
| 名称 | 22.2 二次函数与一元二次方程 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 905.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
22.2 二次函数与一元二次方程
教学目标
知识与技能:二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系;会利用二次函数的图象求一元二次方程的近似解。
过程与方法:通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系。
情感、态度、价值观:通过观察二次函数图象与x轴的交点个数,讨论一元二次方程的根的情况,进一步体会数形结合思想.
教学重难点
教学重点:会利用二次函数的图象求一元二次方程的近似解
教学难点:一元二次方程根的情况与二次函数图象与x轴位置关系的联系,数形结合思想的灵活。
问题: 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线。如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系 h=20t—5t2。
情景导入
考虑以下问题
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?
分析:由于球的飞行高度h与飞行时间t的关系是二次函数
h=20t-5t2。
所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h的值:否则,说明球的飞行高度不能达到问题中h的值。
解:(1)解方程 15=20t—5t2。 t2—4t+3=0。 t1=1,t2=3。
当球飞行1s和3s时,它的高度为15m。
(2)解方程 20=20t-5t2。 t2-4t+4=0。 t1=t2=2。
当球飞行2s时,它的高度为20m。
(3)解方程 20.5=20t-5t2。 t2-4t+4.1=0。
因为(-4)2-4×4.1<0。所以方程无解。球的飞行高度达不到20.5m。
(4)解方程 0=20t-5t2。 t2-4t=0。 t1=0,t2=4。
当球飞行0s和4s时,它的高度为0m,即0s时球从地面飞出。4s时球落回地面。
例如:已知二次函数y=-x2+4x的值为3。求自变量x的值。可以解一元二次方程-x2+4x=3(即x2-4x+3=0) 。反过来,解方程x2-4x+3=0又可以看作已知二次函数y=x2-4+3的值为0,求自变量x的值。
一般地,我们可以利用二次函数y=ax2+bx+c深入讨论一元二次方程ax2+bx+c=0。
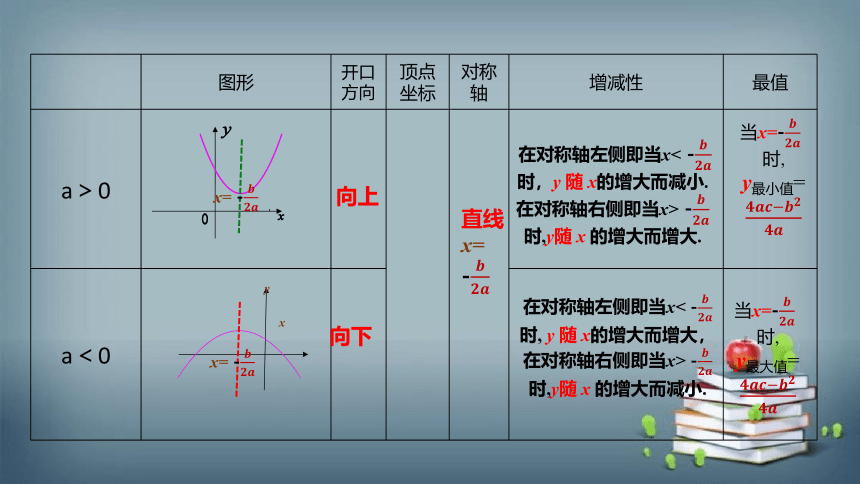
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线x=
-
在对称轴左侧即当x< -时,y 随 x的增大而减小.
在对称轴右侧即当x> -时,y随 x 的增大而增大.
在对称轴左侧即当x< -时, y 随 x的增大而增大,
在对称轴右侧即当x> -时,y随 x 的增大而减小.
当x=-
时,
y最小值=
当x=-
时,
y最大值=
x
y
O
y
x
x= -
x= -
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题一:球的飞行高度能否达到 15 m 若能,需要多少时间
【分析】:由于小球的飞行高度h与飞行时间t有函数关系h=20t-5t2,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.
【注意】根据实际问题,讨论h的取值.
解:当h=15时,20t-5t2=15,
解得,t1=1,t2=3.
当球飞行1s和3s时,它的高度为15m.
探索二次函数与一元二次方程的联系
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题二 球的飞行高度能否达到 20 m 若能,需要多少时间
当h=20时,20t-5t2=20,
解得,t1=t2=2.
当球飞行2s时,它的高度为20m.
探索二次函数与一元二次方程的联系
【提问】结合图形,你知道为什么在问题一中有两个点符合题意,而在问题二中只有一个点符合题意?
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题三 球的飞行高度能否达到 20.5 m 为什么?
探索二次函数与一元二次方程的联系
当h=20.5时,20t-5t2=20.5,
化简得,t2-4t+4.1=0,
因为(-4)2-4×4.1<0,所以方程无实根.
故球的飞行高度达不到20.5m.
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题四 球从飞出到落地要用多少时间
探索二次函数与一元二次方程的联系
当h=0时,20t-5t2=0,
解得,t1=0,t2=4.
当球飞行0s和4s时,它的高度为0m,
即0s时,球从地面飞出,4s时球落回地面.
探索二次函数与一元二次方程的联系
从上面发现,一般地,当 y 取定值且 a≠0 时,二次函数为一元二次方程。如:y=5 时,5=ax2+bx+c 就是一个一元二次方程。所以二次函数与一元二次方程关系密切。
例如:已知二次函数y=-x2+4x的值为3,求自变量x 的值。就是求方程3=-x2+4x(即x2-4x+3=0)的解。
反过来,解方程x2-4x+3=0,就是已知二次函数y=x2-4x+3的值为0,求自变量x的值。
探索二次函数与一元二次方程的联系
解题技巧
1.画出下列二次函数图象
1)y=x2+x-2;
2)y=x2-6x+9;
3)y=x2-x+1,
2.你得出相应的一元二次方程的解吗
6
5
4
3
2
1
-1
-2
-3
-4
x
O
-4 -3 -2 -1 1 2 3 4 5 6
6
5
4
3
2
1
-1
-2
-3
-4
二次函数 y=x2+x-2 y=x2-6x+9 y=x2-x+1
与x轴交点坐标 (-2,0),(1,0) (3,0) 无交点
相应方程的根 x1=-2,x2=1 x1=x2=3 无实根
y=x2+x-2
探索二次函数和x轴公共点与一元二次方程的根的关系
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系
抛物线y=ax2+bx+c(a≠0) 与x轴的公共点的个数 一元二次方程ax2+bx+c=0
(a≠0)的根的情况
b2-4ac>0 有两个 有两个不相等的实数根
b2-4ac=0 有一个 有两个相等的实数根
b2-4ac<0 没有公共点 没有实数根
判别式(△) b2-4ac 二次函数 y=ax2+bx+c(a≠0) 图象 一元二次方程ax2+bx+c=0(a≠0)的根
b2-4ac>0
b2-4ac=0
b2-4ac<0
与x轴有两个不同的交点
(x1,0)(x2,0)
与x轴没有交点
x
y
O
x
y
O
x
y
O
有两个不同的解x=x1,x=x2
没有实数根
有两个重合的公共点
有两个相等的实数根
探索二次函数和x轴公共点与一元二次方程的根的关系
图象伐解一元二次方程
由上面的结论,我们可以利用二次函数的图象求一元二次方程的根。由于作图或观察可能存在误差,由图象求得的根,一般是近似的。
例:利用函数图象求方程的实数根(结果保留小数后一位)。
解:如右图它与x轴的公共点的横坐标
大致为-0.7,2.7。
所以方程的实数根为:
探索二次函数与一元二次方程的联系
P(2,-2)
P’(3,1)
重复上述过程,不断缩小根的范围,根所在两端的值就越来越接近根的值.因而可以作为根的近似值。
当x=2时,y=-2(点(2,-2)在x轴下方);
当x=3时,y= 1(点(3, 1)在x轴上方) ;
而二次函数是一条连续不断的曲线,
所以二次函数在2即方程在在2P(2,-2)
P’(3,1)
尝求出方程
(求抛物线与坐标轴交点)
典例1.抛物线与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
变式1-1.已知二次函数y=x2﹣5x+m的图象与x轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为( )
A.(﹣1,0) B.(4,0) C.(5,0) D.(﹣6,0)
变式1-2 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
变式1-3 抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),则这条抛物线的对称轴是( )
A.直线x=-1 B.直线x=0 C.直线x=1 D.直线x=3
(求抛物线与坐标轴交点)
变式1-4如图二次函数的图象交轴于,两点,交轴于,则的面积为( )
A. B. C. D.
【详解】解:在中,
当时,、;
当时,;
即、、
故的面积为:;
故选C.
(求抛物线与坐标轴交点)
变式1-5 在图中画出函数y=x2-2x-3的图象,利用图象回答:
(1)方程x2-2x-3=0的解是多少;
(2) x取什么值时,函数值大于0;
(3) x取什么值时,函数值小于0.
解:图象如图所示.
(1) 方程x2-2x-3=0的解为x1=-1,x2=3.
(2) x>3或x<-1时,函数值大于0.
(3) -13
y
O
-3
3
x
(已知二次函数函数值求自变量的值)
典例2.根据下面表格中的对应值:
x 3.23 3.24 3.25 3.26
ax2+bx+c -0.06 -0.02 0.03 0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A.3<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
【详解】解:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,
函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=-0.02与y=0.03之间,
∴对应的x的值在3.24与3.25之间即3.24<x<3.25.故选C.
(已知二次函数函数值求自变量的值)
变式2-1.若抛物线的对称轴是直线,则方程 =5的解是( )
A., B.,
C., D.,
【详解】解:由题意: ,解得:b=-4
∴ =5
解得:,,故选:C
(抛物线与x轴有交点,求未知数取值范围)
典例3.已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点,则m的取值范围是( )
A.m≤5 B.m≥2 C.m<5 D.m>2
【详解】∵二次函数y=x2﹣x+m﹣1的图象与x轴有交点,
∴△=(-1) 2-4×1×( m-1)≥0,
解得:m≤5,故选A.
(抛物线与x轴有交点,求未知数取值范围)
变式3-1.已知函数的图象与x轴有交点.则的取值范围是( )
A.k<4 B.k≤4
C.k<4且k≠3 D.k≤4且k≠3
【解析】若此函数与x轴有交点,则,Δ≥0,即4-4(k-3)≥0,解得:k≤4,当k=3时,此函数为一次函数,题目要求仍然成立,故本题选B.
(图像法确定一元二次方程近似根)
典例4 下列表格是二次函数的自变量x与函数值y的对应值,判断方程(为常数)的一个解x的范围是()
A. B.
C. D.
【详解】
利用二次函数和一元二次方程的性质.
由表格中的数据看出-0.01和0.02更接近于0,故x应取对应的范围.
故选C.
二次函数与一元二次方程
二次函数与一元二次方程的关系
有两个交点
根据函数图象求一元二次方程的近似解
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
22.2 二次函数与一元二次方程
教学目标
知识与技能:二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系;会利用二次函数的图象求一元二次方程的近似解。
过程与方法:通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系。
情感、态度、价值观:通过观察二次函数图象与x轴的交点个数,讨论一元二次方程的根的情况,进一步体会数形结合思想.
教学重难点
教学重点:会利用二次函数的图象求一元二次方程的近似解
教学难点:一元二次方程根的情况与二次函数图象与x轴位置关系的联系,数形结合思想的灵活。
问题: 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线。如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系 h=20t—5t2。
情景导入
考虑以下问题
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?
分析:由于球的飞行高度h与飞行时间t的关系是二次函数
h=20t-5t2。
所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h的值:否则,说明球的飞行高度不能达到问题中h的值。
解:(1)解方程 15=20t—5t2。 t2—4t+3=0。 t1=1,t2=3。
当球飞行1s和3s时,它的高度为15m。
(2)解方程 20=20t-5t2。 t2-4t+4=0。 t1=t2=2。
当球飞行2s时,它的高度为20m。
(3)解方程 20.5=20t-5t2。 t2-4t+4.1=0。
因为(-4)2-4×4.1<0。所以方程无解。球的飞行高度达不到20.5m。
(4)解方程 0=20t-5t2。 t2-4t=0。 t1=0,t2=4。
当球飞行0s和4s时,它的高度为0m,即0s时球从地面飞出。4s时球落回地面。
例如:已知二次函数y=-x2+4x的值为3。求自变量x的值。可以解一元二次方程-x2+4x=3(即x2-4x+3=0) 。反过来,解方程x2-4x+3=0又可以看作已知二次函数y=x2-4+3的值为0,求自变量x的值。
一般地,我们可以利用二次函数y=ax2+bx+c深入讨论一元二次方程ax2+bx+c=0。
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
直线x=
-
在对称轴左侧即当x< -时,y 随 x的增大而减小.
在对称轴右侧即当x> -时,y随 x 的增大而增大.
在对称轴左侧即当x< -时, y 随 x的增大而增大,
在对称轴右侧即当x> -时,y随 x 的增大而减小.
当x=-
时,
y最小值=
当x=-
时,
y最大值=
x
y
O
y
x
x= -
x= -
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题一:球的飞行高度能否达到 15 m 若能,需要多少时间
【分析】:由于小球的飞行高度h与飞行时间t有函数关系h=20t-5t2,所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方程.
【注意】根据实际问题,讨论h的取值.
解:当h=15时,20t-5t2=15,
解得,t1=1,t2=3.
当球飞行1s和3s时,它的高度为15m.
探索二次函数与一元二次方程的联系
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题二 球的飞行高度能否达到 20 m 若能,需要多少时间
当h=20时,20t-5t2=20,
解得,t1=t2=2.
当球飞行2s时,它的高度为20m.
探索二次函数与一元二次方程的联系
【提问】结合图形,你知道为什么在问题一中有两个点符合题意,而在问题二中只有一个点符合题意?
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题三 球的飞行高度能否达到 20.5 m 为什么?
探索二次函数与一元二次方程的联系
当h=20.5时,20t-5t2=20.5,
化简得,t2-4t+4.1=0,
因为(-4)2-4×4.1<0,所以方程无实根.
故球的飞行高度达不到20.5m.
以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线是一条抛物线,如果不考虑空气阻力,球的飞行高度 h (单位:m)与飞行时间t (单位:s)之间具有关系:h= 20t–5t2 .
考虑下列问题:
问题四 球从飞出到落地要用多少时间
探索二次函数与一元二次方程的联系
当h=0时,20t-5t2=0,
解得,t1=0,t2=4.
当球飞行0s和4s时,它的高度为0m,
即0s时,球从地面飞出,4s时球落回地面.
探索二次函数与一元二次方程的联系
从上面发现,一般地,当 y 取定值且 a≠0 时,二次函数为一元二次方程。如:y=5 时,5=ax2+bx+c 就是一个一元二次方程。所以二次函数与一元二次方程关系密切。
例如:已知二次函数y=-x2+4x的值为3,求自变量x 的值。就是求方程3=-x2+4x(即x2-4x+3=0)的解。
反过来,解方程x2-4x+3=0,就是已知二次函数y=x2-4x+3的值为0,求自变量x的值。
探索二次函数与一元二次方程的联系
解题技巧
1.画出下列二次函数图象
1)y=x2+x-2;
2)y=x2-6x+9;
3)y=x2-x+1,
2.你得出相应的一元二次方程的解吗
6
5
4
3
2
1
-1
-2
-3
-4
x
O
-4 -3 -2 -1 1 2 3 4 5 6
6
5
4
3
2
1
-1
-2
-3
-4
二次函数 y=x2+x-2 y=x2-6x+9 y=x2-x+1
与x轴交点坐标 (-2,0),(1,0) (3,0) 无交点
相应方程的根 x1=-2,x2=1 x1=x2=3 无实根
y=x2+x-2
探索二次函数和x轴公共点与一元二次方程的根的关系
二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系
抛物线y=ax2+bx+c(a≠0) 与x轴的公共点的个数 一元二次方程ax2+bx+c=0
(a≠0)的根的情况
b2-4ac>0 有两个 有两个不相等的实数根
b2-4ac=0 有一个 有两个相等的实数根
b2-4ac<0 没有公共点 没有实数根
判别式(△) b2-4ac 二次函数 y=ax2+bx+c(a≠0) 图象 一元二次方程ax2+bx+c=0(a≠0)的根
b2-4ac>0
b2-4ac=0
b2-4ac<0
与x轴有两个不同的交点
(x1,0)(x2,0)
与x轴没有交点
x
y
O
x
y
O
x
y
O
有两个不同的解x=x1,x=x2
没有实数根
有两个重合的公共点
有两个相等的实数根
探索二次函数和x轴公共点与一元二次方程的根的关系
图象伐解一元二次方程
由上面的结论,我们可以利用二次函数的图象求一元二次方程的根。由于作图或观察可能存在误差,由图象求得的根,一般是近似的。
例:利用函数图象求方程的实数根(结果保留小数后一位)。
解:如右图它与x轴的公共点的横坐标
大致为-0.7,2.7。
所以方程的实数根为:
探索二次函数与一元二次方程的联系
P(2,-2)
P’(3,1)
重复上述过程,不断缩小根的范围,根所在两端的值就越来越接近根的值.因而可以作为根的近似值。
当x=2时,y=-2(点(2,-2)在x轴下方);
当x=3时,y= 1(点(3, 1)在x轴上方) ;
而二次函数是一条连续不断的曲线,
所以二次函数在2
P’(3,1)
尝求出方程
(求抛物线与坐标轴交点)
典例1.抛物线与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
变式1-1.已知二次函数y=x2﹣5x+m的图象与x轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为( )
A.(﹣1,0) B.(4,0) C.(5,0) D.(﹣6,0)
变式1-2 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
变式1-3 抛物线y=ax2+bx+c与x轴的公共点是(-1,0),(3,0),则这条抛物线的对称轴是( )
A.直线x=-1 B.直线x=0 C.直线x=1 D.直线x=3
(求抛物线与坐标轴交点)
变式1-4如图二次函数的图象交轴于,两点,交轴于,则的面积为( )
A. B. C. D.
【详解】解:在中,
当时,、;
当时,;
即、、
故的面积为:;
故选C.
(求抛物线与坐标轴交点)
变式1-5 在图中画出函数y=x2-2x-3的图象,利用图象回答:
(1)方程x2-2x-3=0的解是多少;
(2) x取什么值时,函数值大于0;
(3) x取什么值时,函数值小于0.
解:图象如图所示.
(1) 方程x2-2x-3=0的解为x1=-1,x2=3.
(2) x>3或x<-1时,函数值大于0.
(3) -1
y
O
-3
3
x
(已知二次函数函数值求自变量的值)
典例2.根据下面表格中的对应值:
x 3.23 3.24 3.25 3.26
ax2+bx+c -0.06 -0.02 0.03 0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A.3<x<3.23 B.3.23<x<3.24
C.3.24<x<3.25 D.3.25<x<3.26
【详解】解:函数y=ax2+bx+c的图象与x轴的交点就是方程ax2+bx+c=0的根,
函数y=ax2+bx+c的图象与x轴的交点的纵坐标为0;
由表中数据可知:y=0在y=-0.02与y=0.03之间,
∴对应的x的值在3.24与3.25之间即3.24<x<3.25.故选C.
(已知二次函数函数值求自变量的值)
变式2-1.若抛物线的对称轴是直线,则方程 =5的解是( )
A., B.,
C., D.,
【详解】解:由题意: ,解得:b=-4
∴ =5
解得:,,故选:C
(抛物线与x轴有交点,求未知数取值范围)
典例3.已知二次函数y=x2﹣x+m﹣1的图象与x轴有交点,则m的取值范围是( )
A.m≤5 B.m≥2 C.m<5 D.m>2
【详解】∵二次函数y=x2﹣x+m﹣1的图象与x轴有交点,
∴△=(-1) 2-4×1×( m-1)≥0,
解得:m≤5,故选A.
(抛物线与x轴有交点,求未知数取值范围)
变式3-1.已知函数的图象与x轴有交点.则的取值范围是( )
A.k<4 B.k≤4
C.k<4且k≠3 D.k≤4且k≠3
【解析】若此函数与x轴有交点,则,Δ≥0,即4-4(k-3)≥0,解得:k≤4,当k=3时,此函数为一次函数,题目要求仍然成立,故本题选B.
(图像法确定一元二次方程近似根)
典例4 下列表格是二次函数的自变量x与函数值y的对应值,判断方程(为常数)的一个解x的范围是()
A. B.
C. D.
【详解】
利用二次函数和一元二次方程的性质.
由表格中的数据看出-0.01和0.02更接近于0,故x应取对应的范围.
故选C.
二次函数与一元二次方程
二次函数与一元二次方程的关系
有两个交点
根据函数图象求一元二次方程的近似解
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
同课章节目录
