22.3.2 实际问题与一元二次函数(2) 课件(共22张PPT)
文档属性
| 名称 | 22.3.2 实际问题与一元二次函数(2) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 887.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
22.3.2 实际问题与一元二次函数(2)
教学目标
1、通过观察、分析、概括、总结等方法了解二次函数面积问题的基本类型,并掌握二次函数中面积问题的相关计算,从而体会方程思想、函数思想、化归思想在二次函数中的应用。
2、由简单题入手逐渐提升,从而消除学生的畏难情绪,让学生有兴趣和积极性参与数学活动。
3、提高学生的归纳总结能力,培养学生不断反思的习惯。
教学重难点
重点:选择方法求图形面积。
难点:如何割补图形求面积。
例1:如图,抛物线经过A(1,0),B(4,0), C(0,-4)三点。P是抛物线的顶点.
(1)求该抛物线的解析式及点P的坐标;
(2)求△PAB的面积。
(3)求△PBC的面积。
与第(2)相比,难度有所提升,但是学生的经验不难得出三边均不在坐标轴上的三角形及不规则多边形需把图形分解(即采用割或补的方法把它分解成易于求出面积的图形)。
补充:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h)。
我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah
即三角形面积等于水平宽与铅垂高乘积的一半.
请证明这个面积计算方法。
变式一: 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点。点D是直线BC上方的抛物线上一个动点,连结DC,DB,若△BCD的面积等于3,求点D的坐标。
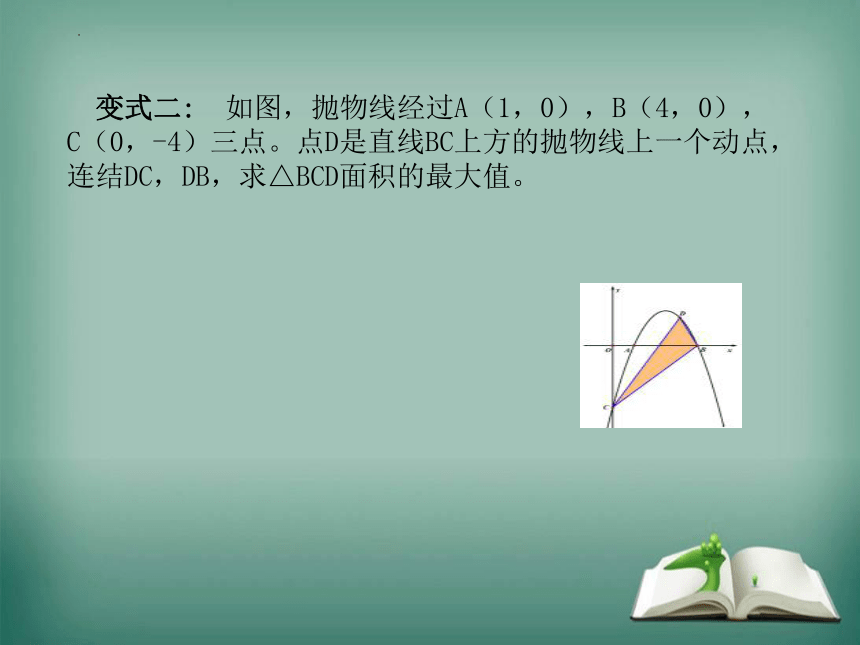
变式二: 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点。点D是直线BC上方的抛物线上一个动点,连结DC,DB,求△BCD面积的最大值。
总结回顾
1、求图形面积方法的选择;
2、数学思想的小结;
3、由二次函数中的面积问题延伸到所有的面积问题。
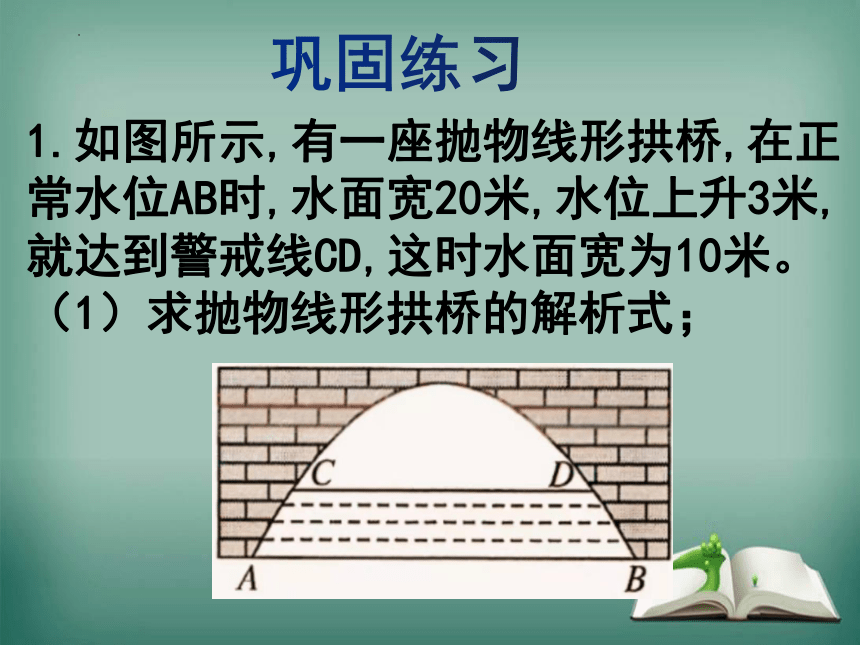
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
x
y
O
(10,m)
(5,m+3)
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
解:(1)设这条抛物线表示的二次函数为y=ax2.
可得,
这条抛物线表示的二次函数为y= - x2.
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
巩固练习
x
y
O
(10,m)
(5,m+3)
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
巩固练习
(2)∵m=-4,∴m+3=-1,
警戒线CD到拱桥顶的距离是1.
1÷0.2=5(小时),
所以从警戒线开始,再持续5小时就能达到拱桥顶.
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥
巩固练习
x
y
O
(10,m)
(5,m+3)
8m
E
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥
巩固练习
(3)由题意可得,点E的横坐标是4,
∴把x=4代入y= - x2中,y=- ,
- -(-4)=3.36>2.5
∴小船能安全通过这座桥.
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
巩固练习
解:(1)设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点B(10,-4),可得-4=100a,a=-.
这条抛物线表示的二次函数为y= - x2.
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
18m
E
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
(3)由题意可得,点E的横坐标是9,
∴把x=9代入y= - x2中,y=- ,
- -(-4)+2=2.76(m)
∴当水深超过2.76米时就会影响过往船只在桥下顺利航行.
解: (1) 如以 AB 所在直线为 x 轴,以 AB 的中点为原点建立平面直角坐标系 xoy,如图所示,
则 A( -4,0),B(4,0),C(0,6).
设这条抛物线的解析式为
y=a(x-4)(x+4).
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
随堂检测
解:(2) 由(1)知抛物线的解析式为
y .
当 x=1时,y= .因为4.4+0.5=4.9< ,
所以这辆货车能安全通过这条隧道.
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(2)现有一辆货车的高度是 4.4m,货车的宽度是 2m.为了保证安全,车顶距离隧道顶部至少 0.5m,通过计算说明这辆货车能否安全通过这条隧道.
2m
4.4m
随堂检测
将 C(0,6)的坐标代入,得 -16a=6,所以抛物线的解析式为
y .
课堂总结
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
22.3.2 实际问题与一元二次函数(2)
教学目标
1、通过观察、分析、概括、总结等方法了解二次函数面积问题的基本类型,并掌握二次函数中面积问题的相关计算,从而体会方程思想、函数思想、化归思想在二次函数中的应用。
2、由简单题入手逐渐提升,从而消除学生的畏难情绪,让学生有兴趣和积极性参与数学活动。
3、提高学生的归纳总结能力,培养学生不断反思的习惯。
教学重难点
重点:选择方法求图形面积。
难点:如何割补图形求面积。
例1:如图,抛物线经过A(1,0),B(4,0), C(0,-4)三点。P是抛物线的顶点.
(1)求该抛物线的解析式及点P的坐标;
(2)求△PAB的面积。
(3)求△PBC的面积。
与第(2)相比,难度有所提升,但是学生的经验不难得出三边均不在坐标轴上的三角形及不规则多边形需把图形分解(即采用割或补的方法把它分解成易于求出面积的图形)。
补充:如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h)。
我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah
即三角形面积等于水平宽与铅垂高乘积的一半.
请证明这个面积计算方法。
变式一: 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点。点D是直线BC上方的抛物线上一个动点,连结DC,DB,若△BCD的面积等于3,求点D的坐标。
变式二: 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点。点D是直线BC上方的抛物线上一个动点,连结DC,DB,求△BCD面积的最大值。
总结回顾
1、求图形面积方法的选择;
2、数学思想的小结;
3、由二次函数中的面积问题延伸到所有的面积问题。
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
x
y
O
(10,m)
(5,m+3)
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线形拱桥的解析式;
巩固练习
解:(1)设这条抛物线表示的二次函数为y=ax2.
可得,
这条抛物线表示的二次函数为y= - x2.
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
巩固练习
x
y
O
(10,m)
(5,m+3)
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
巩固练习
(2)∵m=-4,∴m+3=-1,
警戒线CD到拱桥顶的距离是1.
1÷0.2=5(小时),
所以从警戒线开始,再持续5小时就能达到拱桥顶.
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥
巩固练习
x
y
O
(10,m)
(5,m+3)
8m
E
1.如图所示,有一座抛物线形拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥
巩固练习
(3)由题意可得,点E的横坐标是4,
∴把x=4代入y= - x2中,y=- ,
- -(-4)=3.36>2.5
∴小船能安全通过这座桥.
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
巩固练习
解:(1)设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点B(10,-4),可得-4=100a,a=-.
这条抛物线表示的二次函数为y= - x2.
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(1)在如图所示的直角系中,求抛物线的解析式.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
18m
E
2.有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.
(2)设正常水位时桥下的水深为2m,为保证过往船只顺利航行,桥下水面的宽度不得小于18m,求水深超过多少米时,就会影响过往船只在桥下顺利航行.
巩固练习
(3)由题意可得,点E的横坐标是9,
∴把x=9代入y= - x2中,y=- ,
- -(-4)+2=2.76(m)
∴当水深超过2.76米时就会影响过往船只在桥下顺利航行.
解: (1) 如以 AB 所在直线为 x 轴,以 AB 的中点为原点建立平面直角坐标系 xoy,如图所示,
则 A( -4,0),B(4,0),C(0,6).
设这条抛物线的解析式为
y=a(x-4)(x+4).
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
随堂检测
解:(2) 由(1)知抛物线的解析式为
y .
当 x=1时,y= .因为4.4+0.5=4.9< ,
所以这辆货车能安全通过这条隧道.
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(2)现有一辆货车的高度是 4.4m,货车的宽度是 2m.为了保证安全,车顶距离隧道顶部至少 0.5m,通过计算说明这辆货车能否安全通过这条隧道.
2m
4.4m
随堂检测
将 C(0,6)的坐标代入,得 -16a=6,所以抛物线的解析式为
y .
课堂总结
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的解析式;
同课章节目录
