22.1.4 二次函数y=a(x-h)2 k的图像和性质 课件(共31张PPT)
文档属性
| 名称 | 22.1.4 二次函数y=a(x-h)2 k的图像和性质 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
22.1.4 二次函数y=a(x-h) +k的图像和性质
知识点一
二次函数y=a(x-h) +k的图象和性质
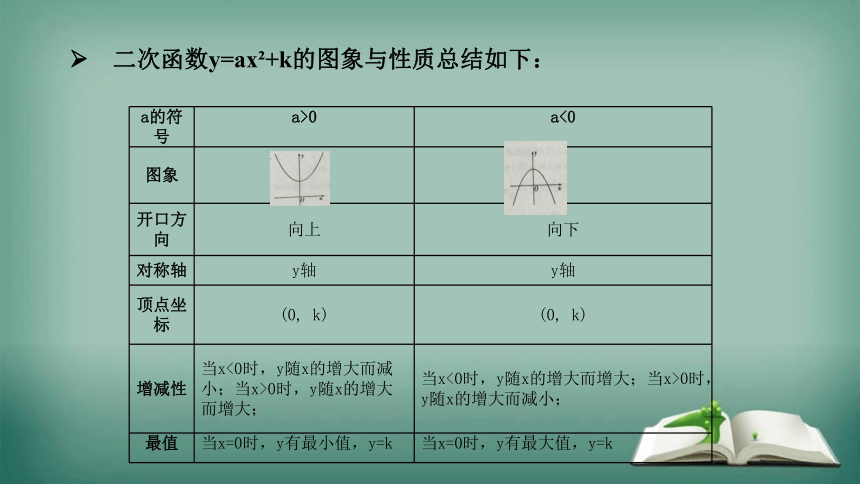
二次函数y=ax +k的图象是一条抛物线,可以看成由y=ax 的图象沿y轴向上(或下)平移
个单位长度得到。
二次函数y=ax +k的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 y轴 y轴
顶点坐标 (0, k) (0, k)
增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大; 当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小;
最值 当x=0时,y有最小值,y=k 当x=0时,y有最大值,y=k
知识点二:二次函数y=a(x-h) 的图象和性质
二次函数y=a(x-h) 的图象是一条抛物线,可以看成由y=ax 的图象向左(或右)平移
个单位长度得到。
二次函数y=a(x-h) 的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 x=h x=h
顶点坐标 (h, 0) (h, 0)
增减性 当xh时,y随x的增大而增大; 当xh时,y随x的增大而减小;
最值 当x=h时,y有最小值,y=0 当x=h时,y有最大值,y=0
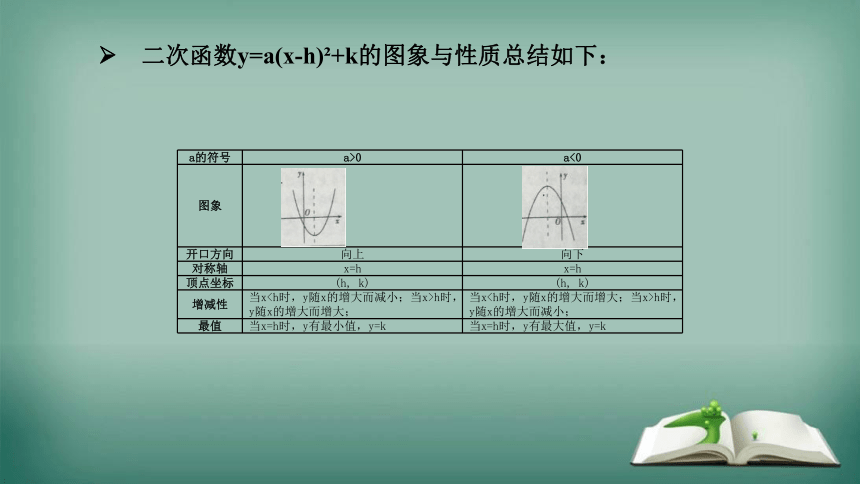
知识点三:二次函数y=a(x-h) +k的图象和性质
二次函数y=a(x-h) +k的图象是一条抛物线,可以看成由y=ax 的图象向左(或右)平移个单位长度,再向上(或下)平移个单位长度得到。
平移的规律可总结为:“作家有减自变量,上加下减常数项”由二次函数y=ax 的图象到y=a(x-h) +k的图象具体的平移过程如下图所示:
二次函数y=a(x-h) +k的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 x=h x=h
顶点坐标 (h, k) (h, k)
增减性 当xh时,y随x的增大而增大; 当xh时,y随x的增大而减小;
最值 当x=h时,y有最小值,y=k 当x=h时,y有最大值,y=k
1
二次函数的顶点式及其图象
二次函数的顶点式是什么意思?
答:
二次函数表达式的第二种表示方法:
对称轴
顶点坐标
最值
与的关系
与
的关系
的作用
时,有最大或者最小值
是向右平移个单位,再向上平移个单位的结果
是配方的结果
顶点的横坐标,也就是对称轴所在的位置;
是顶点的纵坐标,也是函数的最高或最低点.
1
二次函数的顶点式及其图象
二次函数 的图象与二次函数 图象之间的关系
它们的形状(开口大小和方向)相同,只是位置不同,二次函数 的图象可由二次函数 的图象平移得到,即先将二次函数 的图象向左右平移 | 个单位长度,得到二次函数 的图象,再将二次函数 的图象上下平移 | 个单位长度得到二次函数 的图象。
1
二次函数的顶点式及其图象
对二次项系数相同的二次函数,可以根据两抛物线的顶点位置来判断平移的方式,例如抛物线 的顶点坐标是 ,可以看成是把 的图像,先向左平移3个单位长度,再向上平移2个单位长度得到的
从 中可以直接得出抛物线的顶点坐标 ,所以通常把它称为二次函数的顶点式,顶点坐标是
1
二次函数的顶点式及其图象
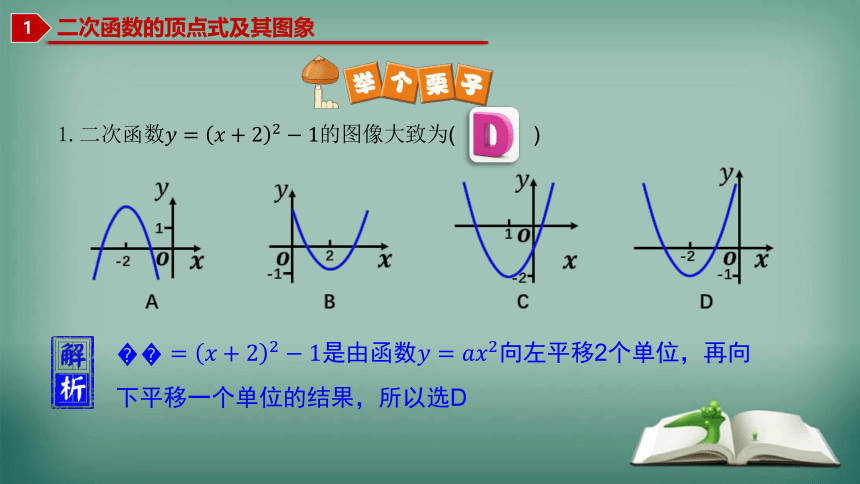
1.二次函数的图像大致为( )
是由函数向左平移2个单位,再向下平移一个单位的结果,所以选D
1
二次函数的顶点式及其图象
2.已知,把它先向右平移2个单位,再向下平移3个单位得到抛物线,则的表达式是多少?
根据“左加右减,上加下减”口诀,
的表达式为
再
1
二次函数的顶点式及其图象
3.已知某个抛物线的顶点坐标为,且经过点,求这个抛物线的表达式.
给了顶点坐标,可以设抛物线的表达式为顶点式,把顶点坐标代入,得,
再把点的坐标代入,得,解得,则抛物线的表达式为
1
二次函数的顶点式及其图象
顶点式与图像
二次函数的配方
2
二次函数的配方
2
二次函数能否配方?怎么配方?配方的结果是什么?
①提取公因式
②配方(配一次项系数
一半[]的平方)
③化简,配方完成
可以配方,方法和一元二次方程的配方法一样,如下图:
二次函数的配方
2
一般式
配方
顶点式
顶点坐标
抛物线从一般式变成了顶点式
二次函数的配方
2
函数形式
表达式
对称轴
顶点坐标
最值
区别关系
字母联系
一般式
顶点式
时,有最值
时,有最值
配方的结果,本质相同
二次函数的配方
2
1.将二次函数转化成的形式,结果为多少?
二次函数的配方
2
2.已知抛物线的对称轴为直线,点M在直线上,
则点M的坐标可能是( )
A. B. C. D.
由表达式可知直线的表达式为,
只有B选项的点的横坐标为3.所以选B
二次函数的配方
2
3.如图所示的二次函数的表达式可能是( )
(1)∵开口朝下,∴;
(2)∵对称轴在轴左边,所以排除A、C【左加右减】;
(3)∵抛物线与轴的交点在下方,∴,排除B,选D
A.
B.
C.
D.
顶点式的不同形式之间的关系
二次函数 之间的关系
位置关系
顶点式的不同形式之间的关系
二次函数 之间的关系
图像和性质关系
顶点式的不同形式之间的关系
抛物线的平移规律是“左加右减,上加下减”,所不同的是左右平移时只针对常数 进行变化,而上下平移时,只针对常数 进行变化。可简记为“左加右减自变量,上加下减常数项”
抛物线 中 的值相等,所以这四条抛物线的形状,大小完全一样,故它们之间可通过互相平移得到
顶点式的不同形式之间的关系
题型
——利用二次函数的对称求交点坐标
题型
——利用二次函数的对称求最小值
题型
——利用二次函数的对称性解决存在性探索问题
题型
——利用二次函数的对称性解决存在性探索问题
22.1.4 二次函数y=a(x-h) +k的图像和性质
知识点一
二次函数y=a(x-h) +k的图象和性质
二次函数y=ax +k的图象是一条抛物线,可以看成由y=ax 的图象沿y轴向上(或下)平移
个单位长度得到。
二次函数y=ax +k的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 y轴 y轴
顶点坐标 (0, k) (0, k)
增减性 当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大; 当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小;
最值 当x=0时,y有最小值,y=k 当x=0时,y有最大值,y=k
知识点二:二次函数y=a(x-h) 的图象和性质
二次函数y=a(x-h) 的图象是一条抛物线,可以看成由y=ax 的图象向左(或右)平移
个单位长度得到。
二次函数y=a(x-h) 的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 x=h x=h
顶点坐标 (h, 0) (h, 0)
增减性 当x
最值 当x=h时,y有最小值,y=0 当x=h时,y有最大值,y=0
知识点三:二次函数y=a(x-h) +k的图象和性质
二次函数y=a(x-h) +k的图象是一条抛物线,可以看成由y=ax 的图象向左(或右)平移个单位长度,再向上(或下)平移个单位长度得到。
平移的规律可总结为:“作家有减自变量,上加下减常数项”由二次函数y=ax 的图象到y=a(x-h) +k的图象具体的平移过程如下图所示:
二次函数y=a(x-h) +k的图象与性质总结如下:
a的符号 a>0 a<0
图象
开口方向 向上 向下
对称轴 x=h x=h
顶点坐标 (h, k) (h, k)
增减性 当x
最值 当x=h时,y有最小值,y=k 当x=h时,y有最大值,y=k
1
二次函数的顶点式及其图象
二次函数的顶点式是什么意思?
答:
二次函数表达式的第二种表示方法:
对称轴
顶点坐标
最值
与的关系
与
的关系
的作用
时,有最大或者最小值
是向右平移个单位,再向上平移个单位的结果
是配方的结果
顶点的横坐标,也就是对称轴所在的位置;
是顶点的纵坐标,也是函数的最高或最低点.
1
二次函数的顶点式及其图象
二次函数 的图象与二次函数 图象之间的关系
它们的形状(开口大小和方向)相同,只是位置不同,二次函数 的图象可由二次函数 的图象平移得到,即先将二次函数 的图象向左右平移 | 个单位长度,得到二次函数 的图象,再将二次函数 的图象上下平移 | 个单位长度得到二次函数 的图象。
1
二次函数的顶点式及其图象
对二次项系数相同的二次函数,可以根据两抛物线的顶点位置来判断平移的方式,例如抛物线 的顶点坐标是 ,可以看成是把 的图像,先向左平移3个单位长度,再向上平移2个单位长度得到的
从 中可以直接得出抛物线的顶点坐标 ,所以通常把它称为二次函数的顶点式,顶点坐标是
1
二次函数的顶点式及其图象
1.二次函数的图像大致为( )
是由函数向左平移2个单位,再向下平移一个单位的结果,所以选D
1
二次函数的顶点式及其图象
2.已知,把它先向右平移2个单位,再向下平移3个单位得到抛物线,则的表达式是多少?
根据“左加右减,上加下减”口诀,
的表达式为
再
1
二次函数的顶点式及其图象
3.已知某个抛物线的顶点坐标为,且经过点,求这个抛物线的表达式.
给了顶点坐标,可以设抛物线的表达式为顶点式,把顶点坐标代入,得,
再把点的坐标代入,得,解得,则抛物线的表达式为
1
二次函数的顶点式及其图象
顶点式与图像
二次函数的配方
2
二次函数的配方
2
二次函数能否配方?怎么配方?配方的结果是什么?
①提取公因式
②配方(配一次项系数
一半[]的平方)
③化简,配方完成
可以配方,方法和一元二次方程的配方法一样,如下图:
二次函数的配方
2
一般式
配方
顶点式
顶点坐标
抛物线从一般式变成了顶点式
二次函数的配方
2
函数形式
表达式
对称轴
顶点坐标
最值
区别关系
字母联系
一般式
顶点式
时,有最值
时,有最值
配方的结果,本质相同
二次函数的配方
2
1.将二次函数转化成的形式,结果为多少?
二次函数的配方
2
2.已知抛物线的对称轴为直线,点M在直线上,
则点M的坐标可能是( )
A. B. C. D.
由表达式可知直线的表达式为,
只有B选项的点的横坐标为3.所以选B
二次函数的配方
2
3.如图所示的二次函数的表达式可能是( )
(1)∵开口朝下,∴;
(2)∵对称轴在轴左边,所以排除A、C【左加右减】;
(3)∵抛物线与轴的交点在下方,∴,排除B,选D
A.
B.
C.
D.
顶点式的不同形式之间的关系
二次函数 之间的关系
位置关系
顶点式的不同形式之间的关系
二次函数 之间的关系
图像和性质关系
顶点式的不同形式之间的关系
抛物线的平移规律是“左加右减,上加下减”,所不同的是左右平移时只针对常数 进行变化,而上下平移时,只针对常数 进行变化。可简记为“左加右减自变量,上加下减常数项”
抛物线 中 的值相等,所以这四条抛物线的形状,大小完全一样,故它们之间可通过互相平移得到
顶点式的不同形式之间的关系
题型
——利用二次函数的对称求交点坐标
题型
——利用二次函数的对称求最小值
题型
——利用二次函数的对称性解决存在性探索问题
题型
——利用二次函数的对称性解决存在性探索问题
同课章节目录
