2.4 圆周角 课件(共20张PPT)
文档属性
| 名称 | 2.4 圆周角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 293.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 10:26:58 | ||
图片预览



文档简介
(共20张PPT)
2.4 圆周角
教学目标
1.认识圆周角,掌握圆周角的两个特征;
2.经历探索同弧或等弧所对圆周角与圆心角的关系的过程,体验“观察—猜想—验证—归纳”的过程,初步应用其解决问题;
3.引导学生体会分类的思想、转化等数学思想方法,学会理性的分析思考问题.
教学重难点
教学重点:
经历探索同弧或等弧所对圆周角与圆周角及圆周角与圆心角的关系的过程;
教学难点:
圆周角位置的分类以及一般位置关系与特殊位置关系的相互转化.
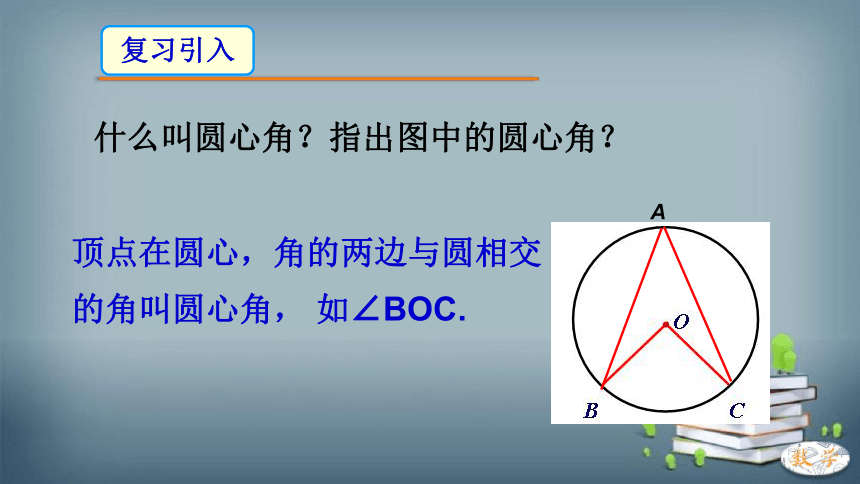
什么叫圆心角?指出图中的圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角, 如∠BOC.
A
复习引入
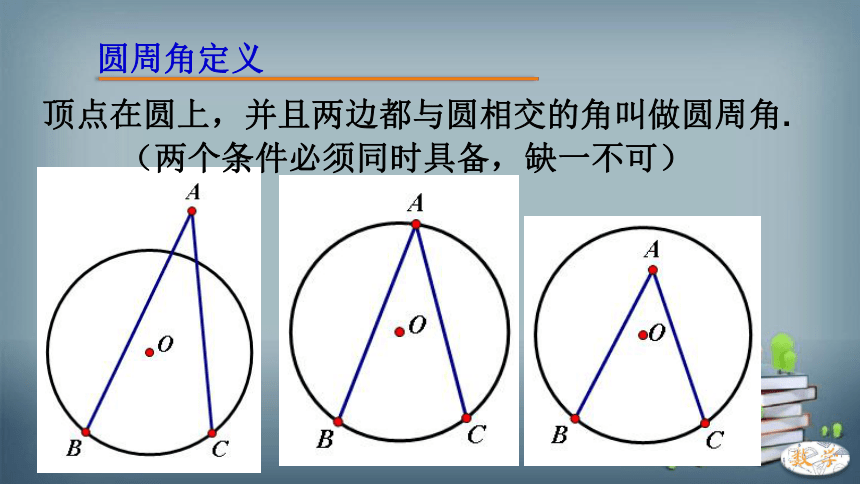
圆周角定义
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
·
C
O
B
A
·
C
O
A
B
·
C
O
B
A
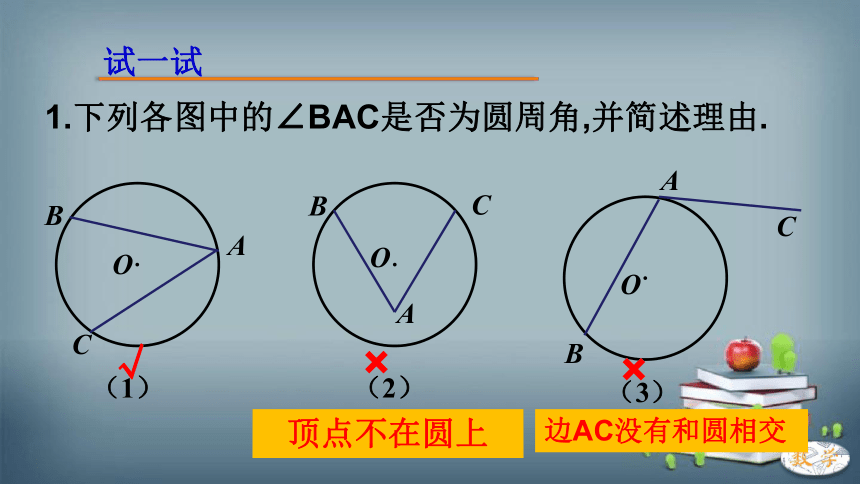
1.下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
顶点不在圆上
边AC没有和圆相交
√
×
×
试一试
·
C
O
A
B
·
C
O
B
A
·
C
O
B
A
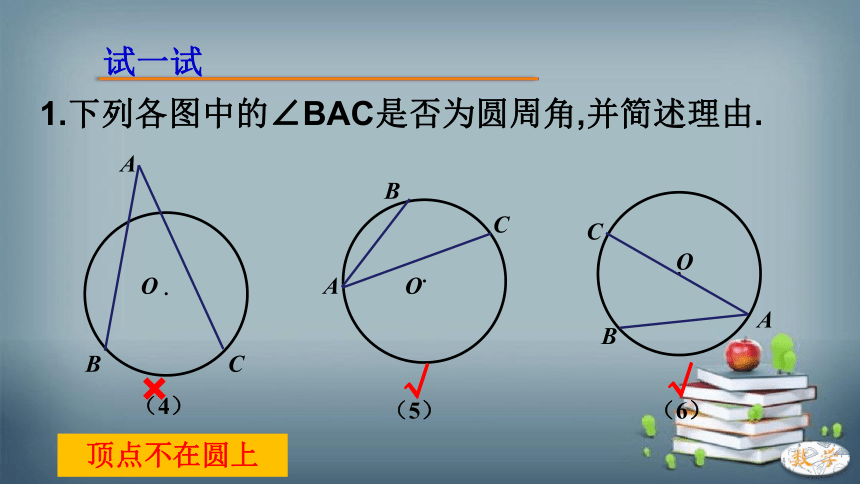
(5)
(6)
顶点不在圆上
1.下列各图中的∠BAC是否为圆周角,并简述理由.
(4)
√
×
√
试一试
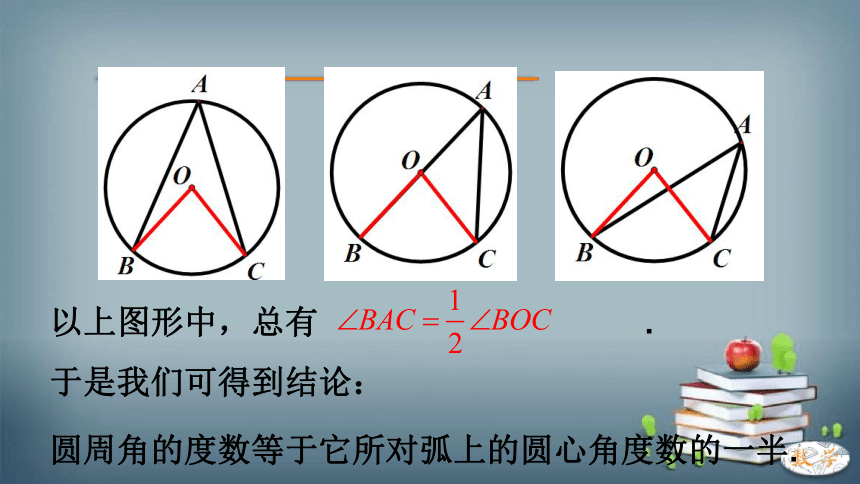
以上图形中,总有 .
于是我们可得到结论:
圆周角的度数等于它所对弧上的圆心角度数的一半.
D
A
O
C
B
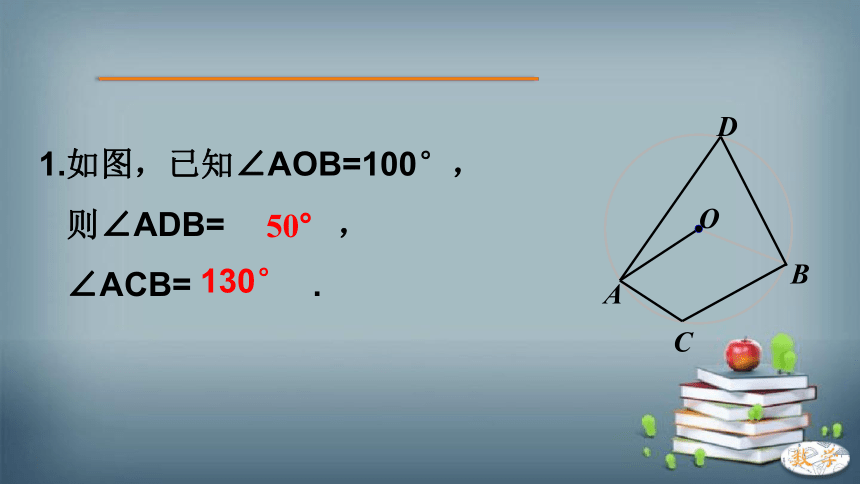
1.如图,已知∠AOB=100°,
则∠ADB= ,
∠ACB= .
50°
130°
C
A
B
O
2.如图,△ABC的顶点A,B,C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
2
3.如图,AB是⊙O的直径,C,D,E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
A1
A2
A3
推论1:
同弧所对的圆周角相等.
圆周角定理及其推论
如图,点A,B,C,D在⊙O上,若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论1:
等弧所对的圆周角相等.
推论1:
同弧或等弧所对的圆周角相等.
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
2.如图,点A,B,C,D在☉O上∠BAC=35 .则∠BOC= , ∠BDC= .
70
35
1.如图,已知⊙O的弦AB直径CD,若∠C=26°,则∠AOD= .
52°
2.如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
C
3.AB是⊙O的弦, C是⊙O上的一点(不与A,B重合),且∠AOB=80°,则∠ACB= .
40°或140°
通过这节课的学习,你又有哪些收获?
课堂小结
再见
2.4 圆周角
教学目标
1.认识圆周角,掌握圆周角的两个特征;
2.经历探索同弧或等弧所对圆周角与圆心角的关系的过程,体验“观察—猜想—验证—归纳”的过程,初步应用其解决问题;
3.引导学生体会分类的思想、转化等数学思想方法,学会理性的分析思考问题.
教学重难点
教学重点:
经历探索同弧或等弧所对圆周角与圆周角及圆周角与圆心角的关系的过程;
教学难点:
圆周角位置的分类以及一般位置关系与特殊位置关系的相互转化.
什么叫圆心角?指出图中的圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角, 如∠BOC.
A
复习引入
圆周角定义
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
·
C
O
B
A
·
C
O
A
B
·
C
O
B
A
1.下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
顶点不在圆上
边AC没有和圆相交
√
×
×
试一试
·
C
O
A
B
·
C
O
B
A
·
C
O
B
A
(5)
(6)
顶点不在圆上
1.下列各图中的∠BAC是否为圆周角,并简述理由.
(4)
√
×
√
试一试
以上图形中,总有 .
于是我们可得到结论:
圆周角的度数等于它所对弧上的圆心角度数的一半.
D
A
O
C
B
1.如图,已知∠AOB=100°,
则∠ADB= ,
∠ACB= .
50°
130°
C
A
B
O
2.如图,△ABC的顶点A,B,C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 .
2
3.如图,AB是⊙O的直径,C,D,E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
A1
A2
A3
推论1:
同弧所对的圆周角相等.
圆周角定理及其推论
如图,点A,B,C,D在⊙O上,若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
推论1:
等弧所对的圆周角相等.
推论1:
同弧或等弧所对的圆周角相等.
1.判断
(1)同一个圆中等弧所对的圆周角相等 ( )
(2)相等的弦所对的圆周角也相等 ( )
(3)同弦所对的圆周角相等 ( )
√
×
×
2.如图,点A,B,C,D在☉O上∠BAC=35 .则∠BOC= , ∠BDC= .
70
35
1.如图,已知⊙O的弦AB直径CD,若∠C=26°,则∠AOD= .
52°
2.如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
C
3.AB是⊙O的弦, C是⊙O上的一点(不与A,B重合),且∠AOB=80°,则∠ACB= .
40°或140°
通过这节课的学习,你又有哪些收获?
课堂小结
再见
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
