19.6反比例函数的图像、性质和应用 课件(共16张PPT)
文档属性
| 名称 | 19.6反比例函数的图像、性质和应用 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
19.6反比例函数的图像、性质和应用
反比例函数的图象是
两支( )
①当k>0时,函数图象位于第( )象限内;
②当k<0时,函数图象位于第( )象限内;
正比例函数的图象是
一条( )
①当k>0时,函数图象位于第( )象限内;
②当k<0时,函数图象位于第( )象限内;
正比例函数
反比例函数
直线
一、三
二、四
曲线
一、三
二、四
复习回顾
回想:正比例函数的性质
当k>0时, y的值随x值的增大而( )
当k<0时, y的值随x值的增大而( )
猜想:反比例函数的性质
当k>0时, 在每个象限内,y的值随x值的增大而( )
当k<0时,在每个象限
内,y的值随x值的增大而( )
增大
增大
减小
减小
复习回顾
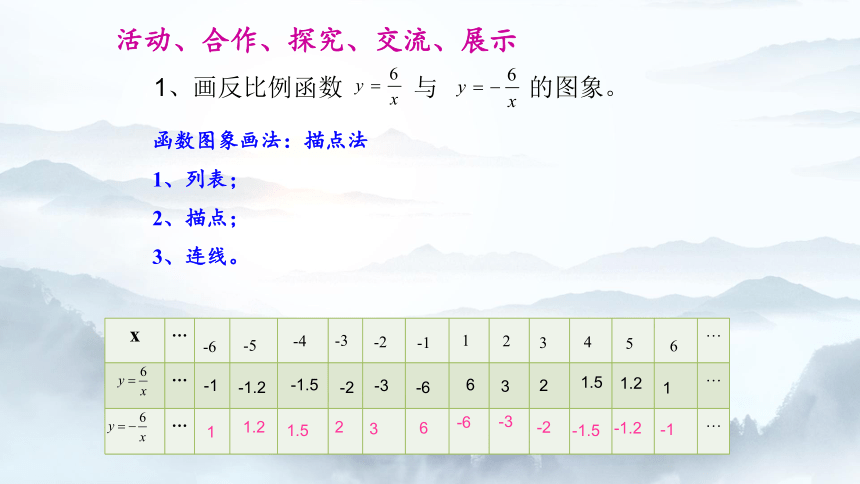
1、画反比例函数 与 的图象。
x … …
… …
… …
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
函数图象画法:描点法
1、列表;
2、描点;
3、连线。
活动、合作、探究、交流、展示
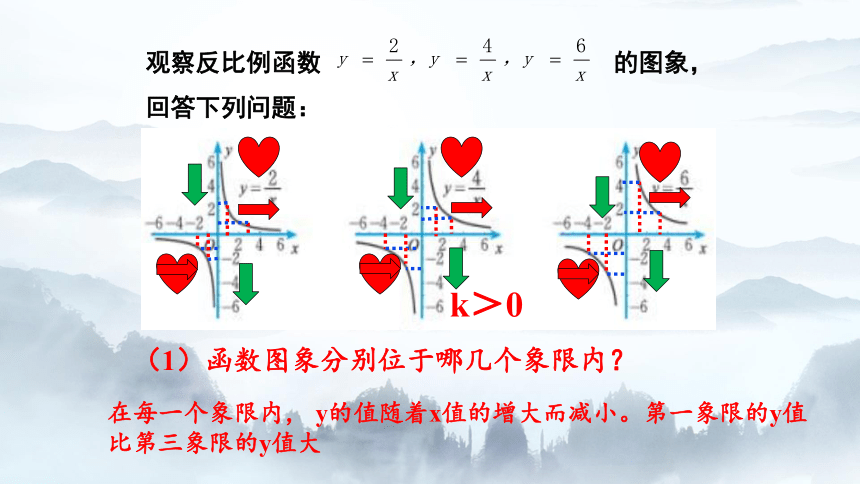
(1)函数图象分别位于哪几个象限内?
观察反比例函数 的图象,回答下列问题:
k>0
在每一个象限内, y的值随着x值的增大而减小。第一象限的y值比第三象限的y值大
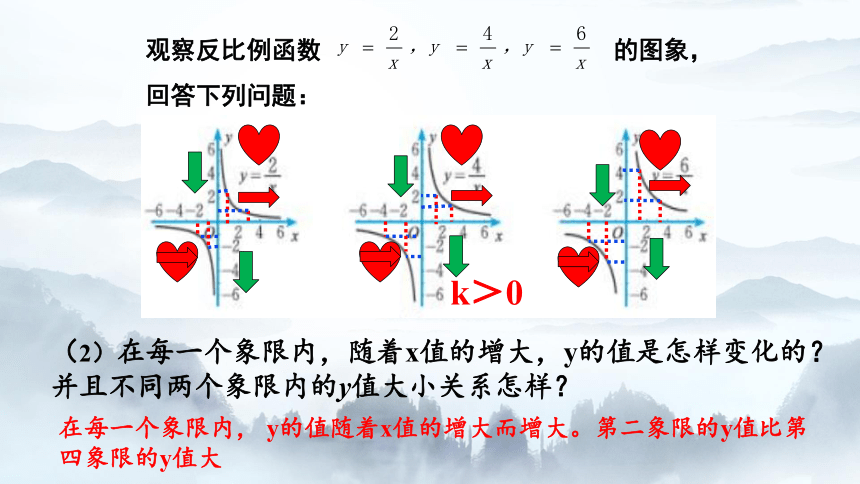
(2)在每一个象限内,随着x值的增大,y的值是怎样变化的?并且不同两个象限内的y值大小关系怎样?
观察反比例函数 的图象,回答下列问题:
k>0
在每一个象限内, y的值随着x值的增大而增大。第二象限的y值比第四象限的y值大
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
观察发现规律,对比生成总结
比较 与 两个图象,它们有什
么共同特点?它们之间有什么关系?
议一议
反比例函数的基本性质
活动、知识提炼
反比例函数(为常数,)图像是_____________.
当 k >0
当k <0
图像
性质
所在象限
增减性
对称性
远近性
双曲线两支
分别在第一、第三象限
双曲线两支
分别在第二、
第四象限
在每个象限内
y随x的增大
而减小;
在每个象限内
y随x的增大
而增大
双曲线
既关于坐标轴成轴对称,又关于原点成中心对称
越大,
图像离坐
标轴越远,
越小,
图像离坐
标轴越近,
但不会与坐
标轴相交.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
认真填一填 (基础题)
2.下列函数:① ;② ;
④ 中
(1)图象位于二、四象限的有 ;
(2)在每一象限内,y的值随x的值增大而增大的有 ;
(3)在每一象限内,y的值随x的值增大而减小的有 .
③
① ②
③ ④
③ ④
4.已知反比例函数y= 的图象过点(1,-2),则k
的值为( )
A.2 B.- C.1 D.-2
D
5.点 , , 均在函数 的图象
上,则y1,y2,y3的大小关系是( )
A. B.
C. D.
D
6.反比例函数 图象上有两个点为( )、
( ),且 ,则下式关系成立的是( )
A. B. C. D.不能确定
D
7.反比例函数 的图象与一次函数y=2x+1的图象的
一个交点是(1,k),则反比例函数的解析式是____.
课堂小结
1.利用反比例函数的图象、性质比较大小,理解反比例系数k的几何意义,并解决相关问题;
2.学会了多角度观察、思考问题;
3.在解决问题的过程中,体会数形结合、分类讨论等思想方法.
作业
1.画出下列函数的图象:
(1)在什么条件下,函数的图象布在第一、第三象限?在什么条 件下,函数的图象布在第二、第四象限?
(2)在什么条件下, y随x的增大而减小?在什么条件下,y随x的增大而增大?
19.6反比例函数的图像、性质和应用
反比例函数的图象是
两支( )
①当k>0时,函数图象位于第( )象限内;
②当k<0时,函数图象位于第( )象限内;
正比例函数的图象是
一条( )
①当k>0时,函数图象位于第( )象限内;
②当k<0时,函数图象位于第( )象限内;
正比例函数
反比例函数
直线
一、三
二、四
曲线
一、三
二、四
复习回顾
回想:正比例函数的性质
当k>0时, y的值随x值的增大而( )
当k<0时, y的值随x值的增大而( )
猜想:反比例函数的性质
当k>0时, 在每个象限内,y的值随x值的增大而( )
当k<0时,在每个象限
内,y的值随x值的增大而( )
增大
增大
减小
减小
复习回顾
1、画反比例函数 与 的图象。
x … …
… …
… …
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
函数图象画法:描点法
1、列表;
2、描点;
3、连线。
活动、合作、探究、交流、展示
(1)函数图象分别位于哪几个象限内?
观察反比例函数 的图象,回答下列问题:
k>0
在每一个象限内, y的值随着x值的增大而减小。第一象限的y值比第三象限的y值大
(2)在每一个象限内,随着x值的增大,y的值是怎样变化的?并且不同两个象限内的y值大小关系怎样?
观察反比例函数 的图象,回答下列问题:
k>0
在每一个象限内, y的值随着x值的增大而增大。第二象限的y值比第四象限的y值大
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
观察发现规律,对比生成总结
比较 与 两个图象,它们有什
么共同特点?它们之间有什么关系?
议一议
反比例函数的基本性质
活动、知识提炼
反比例函数(为常数,)图像是_____________.
当 k >0
当k <0
图像
性质
所在象限
增减性
对称性
远近性
双曲线两支
分别在第一、第三象限
双曲线两支
分别在第二、
第四象限
在每个象限内
y随x的增大
而减小;
在每个象限内
y随x的增大
而增大
双曲线
既关于坐标轴成轴对称,又关于原点成中心对称
越大,
图像离坐
标轴越远,
越小,
图像离坐
标轴越近,
但不会与坐
标轴相交.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
认真填一填 (基础题)
2.下列函数:① ;② ;
④ 中
(1)图象位于二、四象限的有 ;
(2)在每一象限内,y的值随x的值增大而增大的有 ;
(3)在每一象限内,y的值随x的值增大而减小的有 .
③
① ②
③ ④
③ ④
4.已知反比例函数y= 的图象过点(1,-2),则k
的值为( )
A.2 B.- C.1 D.-2
D
5.点 , , 均在函数 的图象
上,则y1,y2,y3的大小关系是( )
A. B.
C. D.
D
6.反比例函数 图象上有两个点为( )、
( ),且 ,则下式关系成立的是( )
A. B. C. D.不能确定
D
7.反比例函数 的图象与一次函数y=2x+1的图象的
一个交点是(1,k),则反比例函数的解析式是____.
课堂小结
1.利用反比例函数的图象、性质比较大小,理解反比例系数k的几何意义,并解决相关问题;
2.学会了多角度观察、思考问题;
3.在解决问题的过程中,体会数形结合、分类讨论等思想方法.
作业
1.画出下列函数的图象:
(1)在什么条件下,函数的图象布在第一、第三象限?在什么条 件下,函数的图象布在第二、第四象限?
(2)在什么条件下, y随x的增大而减小?在什么条件下,y随x的增大而增大?
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
