2.5 三角函数的应用 课件(共16张PPT)
文档属性
| 名称 | 2.5 三角函数的应用 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 840.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
2.5 三角函数的应用
1.巩固用三角函数有关知识解决问题,学会解决坡度、坡角问题.
2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
3.培养学生的数学意识,渗透数形结合的数学思想和方法.
重点:理解坡度和坡角的概念.
难点:利用坡度和坡角等条件,解决有关的实际问题.对于坡度i表示成1∶m的形式学生易疏忽,教学中应着重强调,引起学生的重视.
解直角三角形在实际问题中有着广泛的应用.
如图,一学生要测量校园内一棵水杉树的高度. 他站在距离水杉树 8 m 的 E 处,测得树顶的仰角∠ACD = 52°,已知测角器的架高 CE = 1.6 m,问树高 AB 为多少米?(精确到0.1m)
E
B
D
C
A
52°
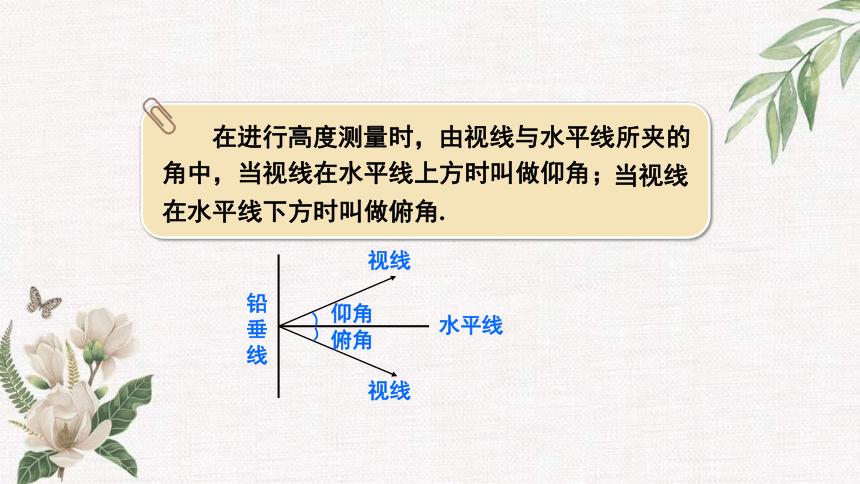
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平线上方时叫做仰角;
当视线在水平线下方时叫做俯角.
铅垂线
水平线
仰角
俯角
视线
视线
E
B
D
C
A
52°
解 在Rt△ACD 中,∠ACD = 52°,CD = EB = 8 m.
由 tan ∠ACD = ,得
AD = CD · tan ∠ACD
= 8×tan 52°
= 8×1.279 9
≈ 10.2(m)
E
B
D
C
A
52°
由 DB = CE = 1.6 m,得
AB = AD + DB
= 10.2 + 1.6
= 11.8(m)
答:树高 AB 为 11.8 m.
例1 如图,铁路路基的横断面是四边形 ABCD. AD∥BC,路基顶宽 BC = 9.8 m,路基高 BE = 5.8 m,斜坡 AB 的坡度 i = 1: 1.6,斜坡 CD 的坡度 i′ = 1: 2.5,求铁路路基下底宽 AD 的值(精确到 0.1 m)与斜坡的坡角 α 和 β (精确到 1°)的值.
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
解 过点 C 作 CF ⊥AD 于点 F,得
CF = BE,EF = BC,∠A = α,∠D = β.
F
∵ BE = 5.8 m, , ,
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
F
∴AE = 1.6×5.8 = 9.28(m),
DF = 2.5×5.8 = 14.5(m).
AD = AE + EF + DF = 9.28 + 9.8 + 14.5 ≈ 33.6(m)
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
F
由 tan α = i = ,tan β = i′ = ,得
α ≈ 32°,β ≈ 22°.
答:铁路路基下底宽为 33.6 m,斜坡的坡角分别为 32°和 22°
例2 已知:在直线 y = kx + b 上有任意两点 P1(x1,y1),P2(x2,y2),这条直线向上方向与 x 轴正方向所夹的锐角为 α.
求证:tan α = = k.
证明 由 α 是锐角,可知直线 y = kx + b 是上升的,即函数 y = kx + b 的值随 x 值的增大而增大.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
如图,设 x1< x2,则 y1<y2. 过点 P1,P2 作 x 轴的垂线,垂足分别为 Q1, Q2,再过点 P1 作 x 轴的平行线P1R 交 P2Q2 于点 R,得
∠P2P1R = α.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
∵ P1,P2 都在直线 y = kx + b上,
∴ y1 = kx1 + b, ①
y2 = kx2 + b. ②
由 ② – ①,得
在△P2P1R 中,
tan α = = =
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
y2 – y1 = k(x2 – x1)
∴ k = .
即 tan α = = k.
谈谈你的收获
2.5 三角函数的应用
1.巩固用三角函数有关知识解决问题,学会解决坡度、坡角问题.
2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
3.培养学生的数学意识,渗透数形结合的数学思想和方法.
重点:理解坡度和坡角的概念.
难点:利用坡度和坡角等条件,解决有关的实际问题.对于坡度i表示成1∶m的形式学生易疏忽,教学中应着重强调,引起学生的重视.
解直角三角形在实际问题中有着广泛的应用.
如图,一学生要测量校园内一棵水杉树的高度. 他站在距离水杉树 8 m 的 E 处,测得树顶的仰角∠ACD = 52°,已知测角器的架高 CE = 1.6 m,问树高 AB 为多少米?(精确到0.1m)
E
B
D
C
A
52°
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平线上方时叫做仰角;
当视线在水平线下方时叫做俯角.
铅垂线
水平线
仰角
俯角
视线
视线
E
B
D
C
A
52°
解 在Rt△ACD 中,∠ACD = 52°,CD = EB = 8 m.
由 tan ∠ACD = ,得
AD = CD · tan ∠ACD
= 8×tan 52°
= 8×1.279 9
≈ 10.2(m)
E
B
D
C
A
52°
由 DB = CE = 1.6 m,得
AB = AD + DB
= 10.2 + 1.6
= 11.8(m)
答:树高 AB 为 11.8 m.
例1 如图,铁路路基的横断面是四边形 ABCD. AD∥BC,路基顶宽 BC = 9.8 m,路基高 BE = 5.8 m,斜坡 AB 的坡度 i = 1: 1.6,斜坡 CD 的坡度 i′ = 1: 2.5,求铁路路基下底宽 AD 的值(精确到 0.1 m)与斜坡的坡角 α 和 β (精确到 1°)的值.
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
解 过点 C 作 CF ⊥AD 于点 F,得
CF = BE,EF = BC,∠A = α,∠D = β.
F
∵ BE = 5.8 m, , ,
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
F
∴AE = 1.6×5.8 = 9.28(m),
DF = 2.5×5.8 = 14.5(m).
AD = AE + EF + DF = 9.28 + 9.8 + 14.5 ≈ 33.6(m)
A
D
E
B
C
α
β
i = 1∶ 1.6
i′ = 1∶ 2.5
9.8
F
由 tan α = i = ,tan β = i′ = ,得
α ≈ 32°,β ≈ 22°.
答:铁路路基下底宽为 33.6 m,斜坡的坡角分别为 32°和 22°
例2 已知:在直线 y = kx + b 上有任意两点 P1(x1,y1),P2(x2,y2),这条直线向上方向与 x 轴正方向所夹的锐角为 α.
求证:tan α = = k.
证明 由 α 是锐角,可知直线 y = kx + b 是上升的,即函数 y = kx + b 的值随 x 值的增大而增大.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
如图,设 x1< x2,则 y1<y2. 过点 P1,P2 作 x 轴的垂线,垂足分别为 Q1, Q2,再过点 P1 作 x 轴的平行线P1R 交 P2Q2 于点 R,得
∠P2P1R = α.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
∵ P1,P2 都在直线 y = kx + b上,
∴ y1 = kx1 + b, ①
y2 = kx2 + b. ②
由 ② – ①,得
在△P2P1R 中,
tan α = = =
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
y2 – y1 = k(x2 – x1)
∴ k = .
即 tan α = = k.
谈谈你的收获
