2022年秋青岛版初中数学九年级上册 2.1 锐角三角比 课件(共16张PPT)
文档属性
| 名称 | 2022年秋青岛版初中数学九年级上册 2.1 锐角三角比 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.1 锐角三角比
1、探索锐角三角比的概念.
2、能叙述锐角三角比的概念,记住三角比的符号,掌握锐角三角比的表示方法.
3、会求直角三角形中指定锐角的三角比.
1.相似三角形的性质
2.勾股定理
3.Rt△ABC 中,斜边是( ),∠A的对边是 ( ), ∠A 的邻边是( ).
A
B
C
回顾思考:
根据现有知识,会解下列各题吗?
(1)已知:在直角三角形中,AC=4,BC=3,
求∠A.
(2)已知:在直角三角形中,AC=4,∠A=25°,
求:BC.
显然,不能。怎么办呢?
A
C
B
┏
生活中的梯子
梯子是我们日常生活中常见的物体.
情境导入
上图为一社区幼儿园的滑梯,为
了确保小朋友在玩耍过程中能更
加安全你能否用你学过的知识
利用钢管为小朋友们将这个滑梯
变得更加牢固呢?
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
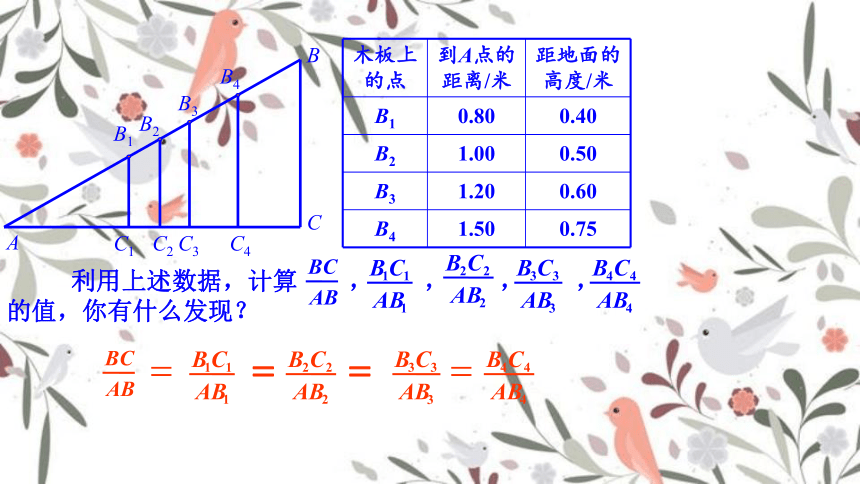
木板上
的点 到A点的
距离/米 距地面的
高度/米
B1 0.80 0.40
B2 1.00 0.50
B3 1.20 0.60
B4 1.50 0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
A
B
C
B1
C1
新知探索
在Rt△ABC中,点B1在斜边AB上,过点B1
作B1C1⊥AC与C1。
求证:(1)△ABC∽△AB1C1
证明:∵B1C1⊥AC
∴∠ACB=∠AC1B1=90°
∵∠A=∠A
∴Rt△ABC∽ Rt△AB1C1
A
B
C
B1
C1
结论:
只要锐角A的度数一定,∠A无论在哪一个直角三角形中,它的对边与斜边的比值都是不变的(定值)。
如图,我们知道:当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其他边之间的比值也确定吗
结论:
在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.
A
B
C
∠A的对边
∠A的邻边
┌
斜边
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
木板上
的点 到A点的
距离/米 距地面的
高度/米
B1 0.80 0.40
B2 1.00 0.50
B3 1.20 0.60
B4 1.50 0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
A
B
C
斜边
∠A的邻边
∠A的对边
由锐角A确定的比 叫做∠A的正弦,
∠A的对边
斜边
sinA =
∠A的对边
斜边
记作sinA,即
由锐角A确定的比 叫做∠A的余弦,
∠A的邻边
斜边
cosA =
∠A的邻边
斜边
记作cosA,即
∠A的对边
∠A的邻边
由锐角A确定的比 叫做∠A的正切,
记作tanA,即
tanA =
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
一个锐角A的三角比只与它的大小有关.
在直角三角形中,锐角A的对边与斜边的比 叫做∠A的正弦;
sinA =
∠A的对边
斜边
记作sinA,即
锐角三角比
正弦:
A
C
B
┏
∠B的正弦怎么表示呢?
结论:梯子的倾斜程度与sin A和cos A有关:
sin A越大,梯子越陡;cos A越小,梯子越陡.
如图,梯子的倾斜程度与sin A和cos A有关吗
A
C2
C1
B2
B1
1、正弦:在直角三角形中,锐角A的对
边与斜边的比叫做∠A的正弦;
sinA =
∠A的对边
斜边
记作sinA,即
一、锐角三角比
A
C
B
┏
2、余弦:在直角三角形中,锐角A的邻边与斜
边的比叫做∠A的余弦;
cosA =
∠A的邻边
斜边
记作cosA,即
3、正切:在直角三角形中,锐角A的对边与邻
边的比叫做∠A的正切。
记作tanA,即
tanA =
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
课堂小结
通过这节课的学习,相信同学们一定学到了不少的新的知识了吧,课下一定要积极的落实,对新学的知识进行复习巩固,对新知识预习
2.1 锐角三角比
1、探索锐角三角比的概念.
2、能叙述锐角三角比的概念,记住三角比的符号,掌握锐角三角比的表示方法.
3、会求直角三角形中指定锐角的三角比.
1.相似三角形的性质
2.勾股定理
3.Rt△ABC 中,斜边是( ),∠A的对边是 ( ), ∠A 的邻边是( ).
A
B
C
回顾思考:
根据现有知识,会解下列各题吗?
(1)已知:在直角三角形中,AC=4,BC=3,
求∠A.
(2)已知:在直角三角形中,AC=4,∠A=25°,
求:BC.
显然,不能。怎么办呢?
A
C
B
┏
生活中的梯子
梯子是我们日常生活中常见的物体.
情境导入
上图为一社区幼儿园的滑梯,为
了确保小朋友在玩耍过程中能更
加安全你能否用你学过的知识
利用钢管为小朋友们将这个滑梯
变得更加牢固呢?
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
木板上
的点 到A点的
距离/米 距地面的
高度/米
B1 0.80 0.40
B2 1.00 0.50
B3 1.20 0.60
B4 1.50 0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
A
B
C
B1
C1
新知探索
在Rt△ABC中,点B1在斜边AB上,过点B1
作B1C1⊥AC与C1。
求证:(1)△ABC∽△AB1C1
证明:∵B1C1⊥AC
∴∠ACB=∠AC1B1=90°
∵∠A=∠A
∴Rt△ABC∽ Rt△AB1C1
A
B
C
B1
C1
结论:
只要锐角A的度数一定,∠A无论在哪一个直角三角形中,它的对边与斜边的比值都是不变的(定值)。
如图,我们知道:当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其他边之间的比值也确定吗
结论:
在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.
A
B
C
∠A的对边
∠A的邻边
┌
斜边
A
B
C
B1
C1
C2
C3
C4
B2
B3
B4
木板上
的点 到A点的
距离/米 距地面的
高度/米
B1 0.80 0.40
B2 1.00 0.50
B3 1.20 0.60
B4 1.50 0.75
利用上述数据,计算 , , , , 的值,你有什么发现?
AB
BC
1
1
1
AB
C
B
2
2
2
AB
C
B
3
3
3
AB
C
B
4
4
4
AB
C
B
4
4
4
AB
C
B
=
3
3
3
AB
C
B
=
2
2
2
AB
C
B
=
1
1
1
AB
C
B
=
AB
BC
A
B
C
斜边
∠A的邻边
∠A的对边
由锐角A确定的比 叫做∠A的正弦,
∠A的对边
斜边
sinA =
∠A的对边
斜边
记作sinA,即
由锐角A确定的比 叫做∠A的余弦,
∠A的邻边
斜边
cosA =
∠A的邻边
斜边
记作cosA,即
∠A的对边
∠A的邻边
由锐角A确定的比 叫做∠A的正切,
记作tanA,即
tanA =
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
一个锐角A的三角比只与它的大小有关.
在直角三角形中,锐角A的对边与斜边的比 叫做∠A的正弦;
sinA =
∠A的对边
斜边
记作sinA,即
锐角三角比
正弦:
A
C
B
┏
∠B的正弦怎么表示呢?
结论:梯子的倾斜程度与sin A和cos A有关:
sin A越大,梯子越陡;cos A越小,梯子越陡.
如图,梯子的倾斜程度与sin A和cos A有关吗
A
C2
C1
B2
B1
1、正弦:在直角三角形中,锐角A的对
边与斜边的比叫做∠A的正弦;
sinA =
∠A的对边
斜边
记作sinA,即
一、锐角三角比
A
C
B
┏
2、余弦:在直角三角形中,锐角A的邻边与斜
边的比叫做∠A的余弦;
cosA =
∠A的邻边
斜边
记作cosA,即
3、正切:在直角三角形中,锐角A的对边与邻
边的比叫做∠A的正切。
记作tanA,即
tanA =
∠A的对边
∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比.
课堂小结
通过这节课的学习,相信同学们一定学到了不少的新的知识了吧,课下一定要积极的落实,对新学的知识进行复习巩固,对新知识预习
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
