2.1 锐角三角函数 课件(共17张PPT)
文档属性
| 名称 | 2.1 锐角三角函数 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 726.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 13:37:25 | ||
图片预览





文档简介
(共17张PPT)
2.1 锐角三角形
1.了解正切函数的概念,能够正确应用tan A表示直角三角形中两边的比,了解坡度的概念.
2.通过正切函数的学习,进一步认识函数,体会函数的变化与对应的思想,逐步培养学生会观察、比较、分析、概括等逻辑思维能力.
重点:
1.掌握锐角的正切的概念,能用直角三角形中两边的比表示锐角的正切.
2.了解坡度的概念,知道坡度越大,坡面越陡.
难点:利用正切的有关知识解决实际生活中的问题.
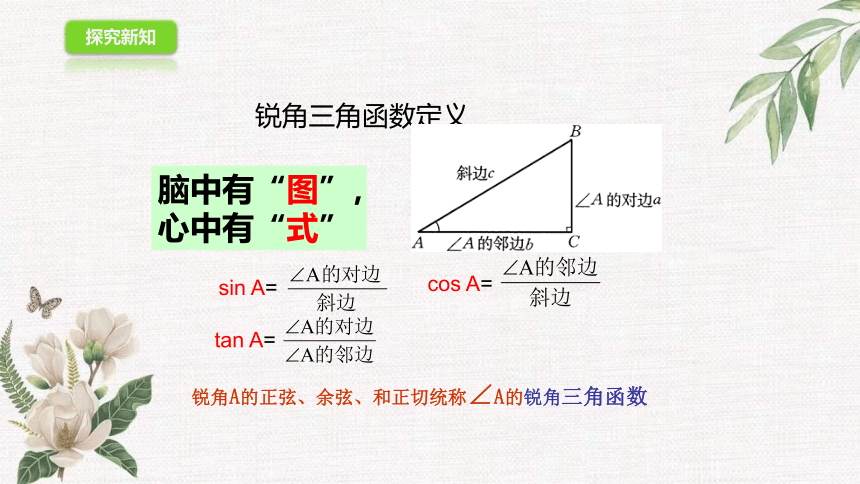
锐角三角函数定义
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数
sin A=
cos A=
tan A=
脑中有“图”,心中有“式”
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
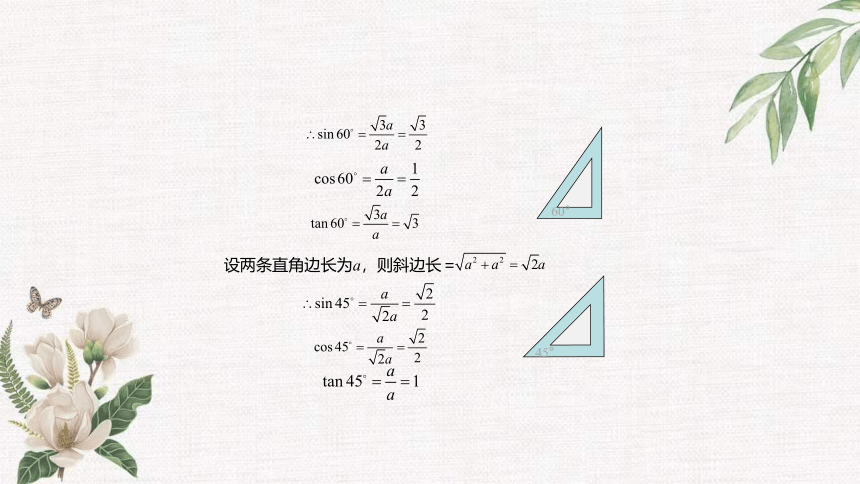
30°、45°、60°角的三角函数
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
设两条直角边长为a,则斜边长=
60°
45°
问题 这个规律是否适合任意一个锐角呢?你能够用所学的知识证明你的结论吗?
提示:使用三角函数的定义证明.
A
C
B
c
a
b
互余两角的正弦、余弦值的关系
一
问题引导
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
b
A
B
C
a
┌
c
∴sinA=cosB,cosA=sinB.
∵∠A+∠B=90°,
∴∠B=90°-∠A,
即sinA=cosB=cos(90°-∠A),
cosA=sinB= sin(90°-∠A).
sinA和cosB有什么关系
sinA=cosB
任意一个锐角的正(余)弦值,等于它的余角的
余(正)弦值.
结论:
例1: 计算:
(1)sin300+cos450;
(2) sin2600+cos2600-tan450.
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解:(1)原式=
(2)原式=
例2 已知cosα= ,α+β=90°,则cosβ=( )
C
解析:∵cosα= ,α+β=90°,∴sinβ=cosα= .设β是一个直角三角形中的锐角,且sinβ= ,设b=3k,c=5k,则另一直角边的长度为a=4k,∴cosβ=
【方法总结】利用互为余角的锐角三角函数关系时,先判断两角关系,然后再寻求锐角三角函数之间的关系.将角放到直角三角形中,画出图形,根据图形设出比例式,表示出各边.
例3:已知:
求∠A,∠B的度数。
解:
B
C
A
谈谈你的收获
2.1 锐角三角形
1.了解正切函数的概念,能够正确应用tan A表示直角三角形中两边的比,了解坡度的概念.
2.通过正切函数的学习,进一步认识函数,体会函数的变化与对应的思想,逐步培养学生会观察、比较、分析、概括等逻辑思维能力.
重点:
1.掌握锐角的正切的概念,能用直角三角形中两边的比表示锐角的正切.
2.了解坡度的概念,知道坡度越大,坡面越陡.
难点:利用正切的有关知识解决实际生活中的问题.
锐角三角函数定义
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数
sin A=
cos A=
tan A=
脑中有“图”,心中有“式”
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
30°、45°、60°角的三角函数
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
设两条直角边长为a,则斜边长=
60°
45°
问题 这个规律是否适合任意一个锐角呢?你能够用所学的知识证明你的结论吗?
提示:使用三角函数的定义证明.
A
C
B
c
a
b
互余两角的正弦、余弦值的关系
一
问题引导
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
b
A
B
C
a
┌
c
∴sinA=cosB,cosA=sinB.
∵∠A+∠B=90°,
∴∠B=90°-∠A,
即sinA=cosB=cos(90°-∠A),
cosA=sinB= sin(90°-∠A).
sinA和cosB有什么关系
sinA=cosB
任意一个锐角的正(余)弦值,等于它的余角的
余(正)弦值.
结论:
例1: 计算:
(1)sin300+cos450;
(2) sin2600+cos2600-tan450.
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
解:(1)原式=
(2)原式=
例2 已知cosα= ,α+β=90°,则cosβ=( )
C
解析:∵cosα= ,α+β=90°,∴sinβ=cosα= .设β是一个直角三角形中的锐角,且sinβ= ,设b=3k,c=5k,则另一直角边的长度为a=4k,∴cosβ=
【方法总结】利用互为余角的锐角三角函数关系时,先判断两角关系,然后再寻求锐角三角函数之间的关系.将角放到直角三角形中,画出图形,根据图形设出比例式,表示出各边.
例3:已知:
求∠A,∠B的度数。
解:
B
C
A
谈谈你的收获
