2.2 30°,45°,60°的三角函数值 课件(共16张PPT)
文档属性
| 名称 | 2.2 30°,45°,60°的三角函数值 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 589.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 13:45:14 | ||
图片预览






文档简介
(共16张PPT)
2.2 30°,45°,60°的三角函数值
教学目标
1.经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系.
2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,并能够用正切进行简单的计算
教学难点
重点:.从现实情境中探索直角三角形的边角关系.
难点:理解正切的意义,并用它来表示两边的比.
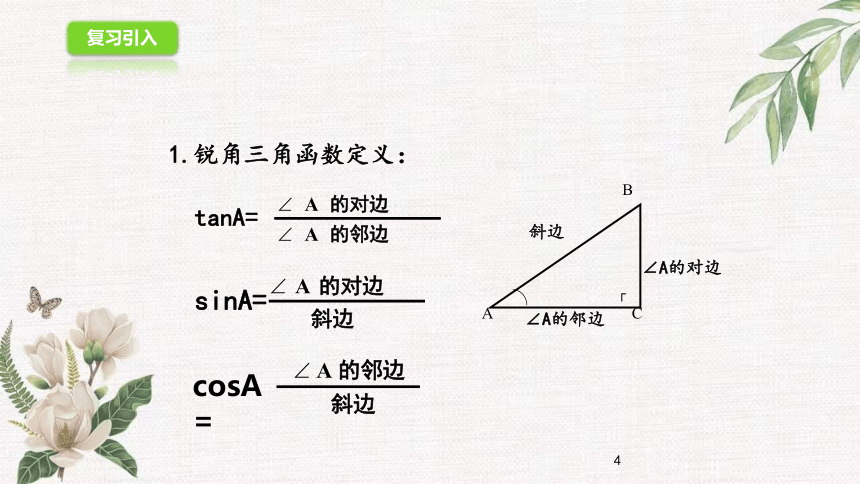
1.锐角三角函数定义:tanA=ABC∠A的对边∠A的邻边┌斜边sinA=cosA=复习引入探究新知
1、锐角三角函数定义
正弦,余弦,正切:
b
A
B
C
a
┌
c
2、互余的两个角之间的三角函数关系
互余两角之间的三角函数关系
b
A
B
C
a
┌
c
∠A+∠B=900.
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin300等于多少
┌
┌
300
600
450
450
(2)cos300等于多少
(3)tan300等于多少
请与同伴交流你是怎么想的 又是怎么做的
◆(4)45°和60°的三角函数值呢?
特殊角的三角函数值表
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
你能发现它们之间有什么联系么
典例精析例1小丽利用有一个锐角为30°的三角尺测量一棵树的高度。已知她与树之间的距离为5m,小丽的身高为1.6m,那么这棵树大约有多高?(结果精确到0.1 m)解:由题意得,四边形ABED是矩形,AB=ED=1.6,AD=BE=5在Rt△ACD中,答:这棵树大约有18.9m。例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为300,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
此处摆角是指秋千摆至最高位置时链子所在的直线与铅垂线之间的夹角
将实际问题数学化.
∴最高位置与最低位置的高度差约为0.34m.
A
C
O
B
D
┌
解:如图,由题意得,
∴AC=OA-OC=2.5-2.165≈0.34(m).
2.5
OA表示最低位置,即铅垂线所在位置,OB表示最高位置,过点B作BC⊥OA于点C
例3 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E、F分别是AB、DC的中点,连接EF,求线段EF的长.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
cos∠ACB=cos30°=
∴∠DCA=∠BCA
∴∠ACB=30°,
∴EF=
=12.
(2)AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E.F分别是AB.DC的中点,
1.如图,已知在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB= ,
则下底BC的长为 __________.
【答案】10
巩固练习
2.计算:
【解析】
课堂小结
谈谈你的收获
2.2 30°,45°,60°的三角函数值
教学目标
1.经历探索直角三角形中边角关系的过程,理解正切的意义和与现实生活的联系.
2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,并能够用正切进行简单的计算
教学难点
重点:.从现实情境中探索直角三角形的边角关系.
难点:理解正切的意义,并用它来表示两边的比.
1.锐角三角函数定义:tanA=ABC∠A的对边∠A的邻边┌斜边sinA=cosA=复习引入探究新知
1、锐角三角函数定义
正弦,余弦,正切:
b
A
B
C
a
┌
c
2、互余的两个角之间的三角函数关系
互余两角之间的三角函数关系
b
A
B
C
a
┌
c
∠A+∠B=900.
如图,观察一副三角板:
它们其中有几个锐角 分别是多少度
(1)sin300等于多少
┌
┌
300
600
450
450
(2)cos300等于多少
(3)tan300等于多少
请与同伴交流你是怎么想的 又是怎么做的
◆(4)45°和60°的三角函数值呢?
特殊角的三角函数值表
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
你能发现它们之间有什么联系么
典例精析例1小丽利用有一个锐角为30°的三角尺测量一棵树的高度。已知她与树之间的距离为5m,小丽的身高为1.6m,那么这棵树大约有多高?(结果精确到0.1 m)解:由题意得,四边形ABED是矩形,AB=ED=1.6,AD=BE=5在Rt△ACD中,答:这棵树大约有18.9m。例2 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为300,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
此处摆角是指秋千摆至最高位置时链子所在的直线与铅垂线之间的夹角
将实际问题数学化.
∴最高位置与最低位置的高度差约为0.34m.
A
C
O
B
D
┌
解:如图,由题意得,
∴AC=OA-OC=2.5-2.165≈0.34(m).
2.5
OA表示最低位置,即铅垂线所在位置,OB表示最高位置,过点B作BC⊥OA于点C
例3 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E、F分别是AB、DC的中点,连接EF,求线段EF的长.
【解析】(1)∵∠B=60°,
∴∠BCD=60°,又
∵AB=AD=DC
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
cos∠ACB=cos30°=
∴∠DCA=∠BCA
∴∠ACB=30°,
∴EF=
=12.
(2)AB=AD=DC=8,∠ACB=30°,∴BC=2AB=16,
∵E.F分别是AB.DC的中点,
1.如图,已知在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB= ,
则下底BC的长为 __________.
【答案】10
巩固练习
2.计算:
【解析】
课堂小结
谈谈你的收获
