2.4 解直角三角形 课件(共16张PPT)
文档属性
| 名称 | 2.4 解直角三角形 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 13:39:28 | ||
图片预览




文档简介
(共16张PPT)
2.4 解直角三角形
1.在实际情境中应用勾股定理、锐角三角函数概念来解直角三角形;
2.能够把实际问题转化为数学问题.
1、会运用三角函数解决与直角三角形有关的简单实际问题.
2、会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题.
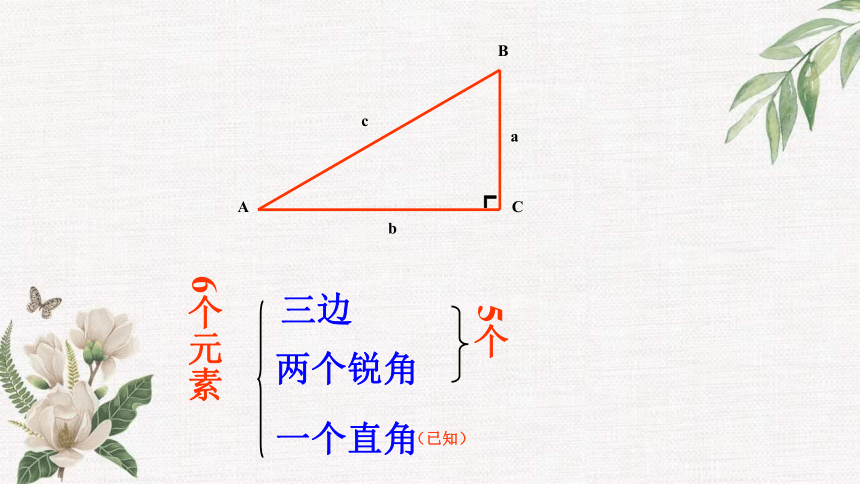
直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
A
B
C
a
b
c
┓
5个
6个元素
三边
两个锐角
一个直角
(已知)
A
B
C
a
b
c
┓
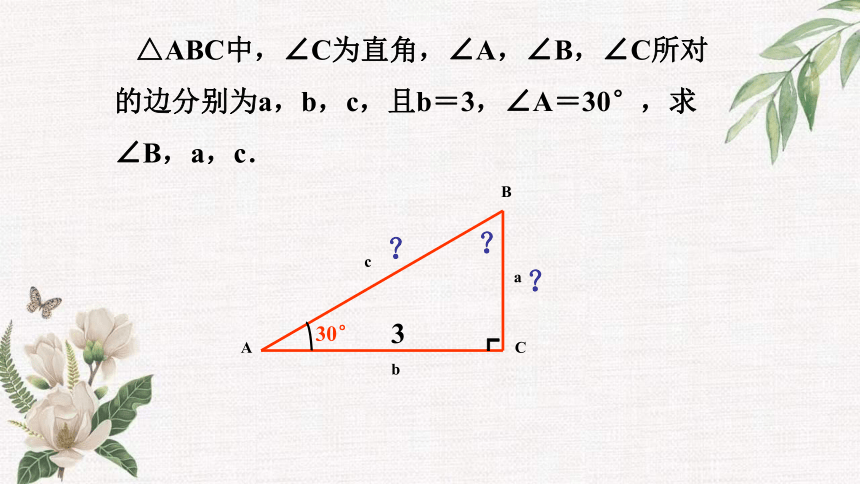
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
?
?
?
┓
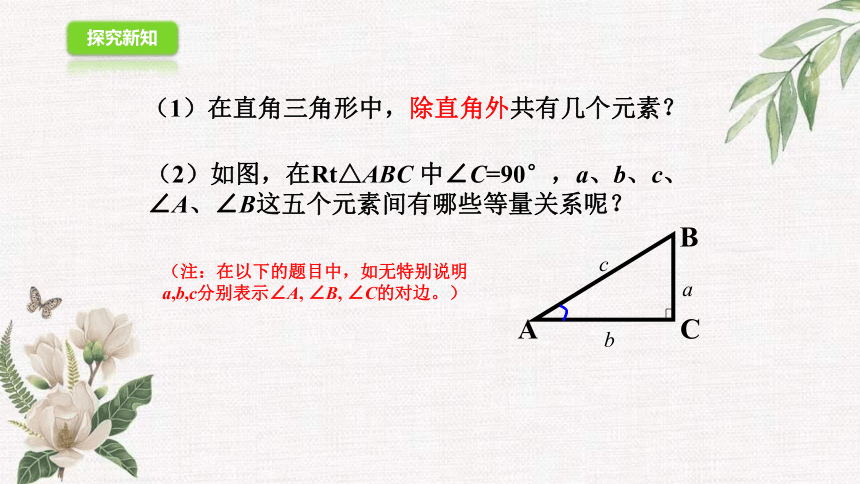
(1)在直角三角形中,除直角外共有几个元素?
A
B
C
c
b
a
(注:在以下的题目中,如无特别说明a,b,c分别表示∠A, ∠B, ∠C的对边。)
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、
∠A、∠B这五个元素间有哪些等量关系呢?
直角三角形中5个元素中,边、角之间有那些等量关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
A
B
C
c
b
a
a2+b2=c2(勾股定理);
∠ A+ ∠ B= 90
解直角三角形的概念:
利用直角三角形边角关系,如果知道直角三角形中的两个元素(其中至少一个是边),就可以求出其他元素。
由直角三角形中已知的元素,求出其他所有未知元素的过程,叫做解直角三角形。
例1 在Rt△ABC 中,已知∠C=90°,a =4 ,
c=8 。解这个直角三角形。
分析:这是已知直角三角形的两边解直角三角形的问题。
要会选择适当的三角比。
4
8
2
2
2
2
=
-
=
-
=
a
c
b
所以
因为
解
,
2
2
2
c
b
a
:
=
+
A
B
C
c
b
a
例2 在Rt△ABC中,已知∠C=90°,a=4, c=8.解这个直角三角形。
解:在Rt△ABC中
B
C
A
a
c
b
∵
∵
例3 在Rt△ABC 中,已知∠C=90°,a =35 ,b=28。求∠A,∠B的度数(结果精确到1°)和c的长(结果保留两位有效数字)。
解:在Rt △ABC 中,
1.在Rt△ABC中,已知∠C=90°,a=4, c=8.解这个直角三角形。
2.在Rt△ABC中,已知∠C=90°,a=b= ,
解这个直角三角形。
B
C
A
a
c
b
3.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
A
4.在下列直角三角形中不能求解的是( )
(A)已知一直角边一锐角
(B)已知一斜边一锐角
(C)已知两边
(D)已知两角
D
在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的。以便于分析解决问题。
选取关系式时要尽量利用原始数据,以防止累积误差。
解直角三角形的方法遵循“有斜用弦,无斜用切”
2.4 解直角三角形
1.在实际情境中应用勾股定理、锐角三角函数概念来解直角三角形;
2.能够把实际问题转化为数学问题.
1、会运用三角函数解决与直角三角形有关的简单实际问题.
2、会综合运用勾股定理、直角三角形的边角关系和角角关系,解决简单的实际问题.
直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
A
B
C
a
b
c
┓
5个
6个元素
三边
两个锐角
一个直角
(已知)
A
B
C
a
b
c
┓
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.
A
B
C
a
b
c
3
30°
?
?
?
┓
(1)在直角三角形中,除直角外共有几个元素?
A
B
C
c
b
a
(注:在以下的题目中,如无特别说明a,b,c分别表示∠A, ∠B, ∠C的对边。)
(2)如图,在Rt△ABC 中∠C=90°,a、b、c、
∠A、∠B这五个元素间有哪些等量关系呢?
直角三角形中5个元素中,边、角之间有那些等量关系:
(1)两锐角关系 :
(2)三边关系:
(3)边与角关系:
A
B
C
c
b
a
a2+b2=c2(勾股定理);
∠ A+ ∠ B= 90
解直角三角形的概念:
利用直角三角形边角关系,如果知道直角三角形中的两个元素(其中至少一个是边),就可以求出其他元素。
由直角三角形中已知的元素,求出其他所有未知元素的过程,叫做解直角三角形。
例1 在Rt△ABC 中,已知∠C=90°,a =4 ,
c=8 。解这个直角三角形。
分析:这是已知直角三角形的两边解直角三角形的问题。
要会选择适当的三角比。
4
8
2
2
2
2
=
-
=
-
=
a
c
b
所以
因为
解
,
2
2
2
c
b
a
:
=
+
A
B
C
c
b
a
例2 在Rt△ABC中,已知∠C=90°,a=4, c=8.解这个直角三角形。
解:在Rt△ABC中
B
C
A
a
c
b
∵
∵
例3 在Rt△ABC 中,已知∠C=90°,a =35 ,b=28。求∠A,∠B的度数(结果精确到1°)和c的长(结果保留两位有效数字)。
解:在Rt △ABC 中,
1.在Rt△ABC中,已知∠C=90°,a=4, c=8.解这个直角三角形。
2.在Rt△ABC中,已知∠C=90°,a=b= ,
解这个直角三角形。
B
C
A
a
c
b
3.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
A
4.在下列直角三角形中不能求解的是( )
(A)已知一直角边一锐角
(B)已知一斜边一锐角
(C)已知两边
(D)已知两角
D
在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的。以便于分析解决问题。
选取关系式时要尽量利用原始数据,以防止累积误差。
解直角三角形的方法遵循“有斜用弦,无斜用切”
