2.5 三角函数的应用 课件(共17张PPT)
文档属性
| 名称 | 2.5 三角函数的应用 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 508.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:56:57 | ||
图片预览





文档简介
(共17张PPT)
2.5 三角函数的应用
1、了解仰角、俯角的概念,能应用解直角三角形解决一类观测实际问题
2、进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角
3.知道直线的斜率与直线和x轴正方向所夹的锐角的正切之间的关系。
4.能综合运用解直角三角形的有关知识解决实际问题。
5.经历探索与梯形、坡比等有关的问题的解法,培养学以致用的意识,和数学建模思想。
重点:了解仰角、俯角的概念,能应用解直角三角形解决一类观测实际问题
难点:进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角
A
C
B
a
b
c
复习三角形的三角函数
sin A = ,sin B = ,
cos A = ,cos B = ,
tan A = ,tan B = .
a
c
a
b
b
c
b
a
b
c
a
c
A
C
B
a
b
c
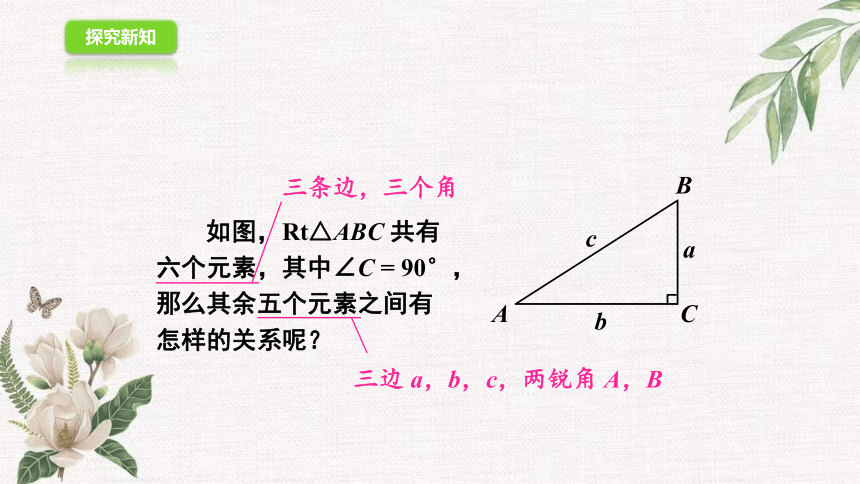
如图,Rt△ABC 共有六个元素,其中∠C = 90°,那么其余五个元素之间有怎样的关系呢?
三条边,三个角
三边 a,b,c,两锐角 A,B
A
C
B
a
b
c
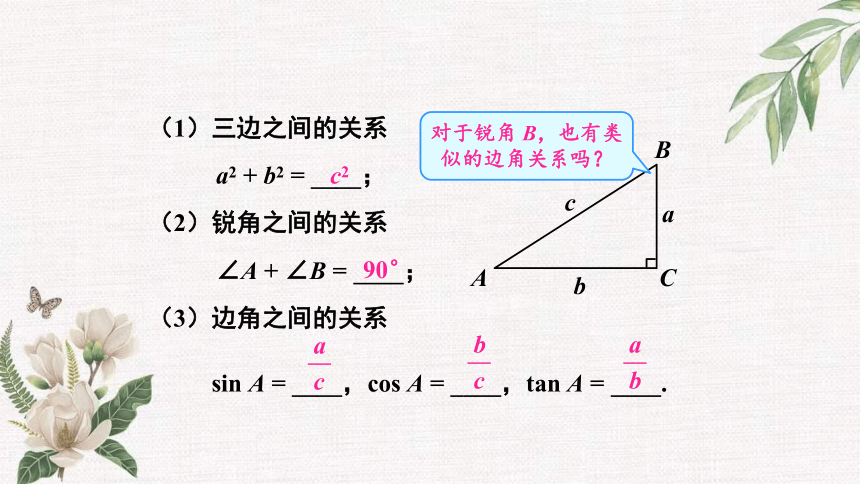
(1)三边之间的关系
a2 + b2 = ____;
(2)锐角之间的关系
∠A + ∠B = ____;
(3)边角之间的关系
sin A = ____,cos A = ____,tan A = ____.
c2
90°
a
c
b
c
a
b
对于锐角 B,也有类似的边角关系吗?
有了以上关系,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
例1 解决本章引言所提问题. 如图,某校九年级学生要测量当地电视塔的高度 AB,因为不能直接到达塔底 B 处,他们采用在发射台院外与电视塔底 B 成一直线的 CD 两处地面上,
A
B
B1
C
D
C1
D1
30°
45°
用测角器测得电视塔顶部 A 的仰角分别为 45°和 30°,同时量得 CD 为 50 m. 已知测角器高为 1 m,问电视塔的高度为多少米?(精确到 1 m)
A
B
B1
C
D
C1
D1
30°
45°
A
B
B1
C
D
C1
D1
30°
45°
解 设 AB1 = x m.
在 Rt△AC1B1 中,由∠AC1B1 = 45°,得
C1B1 = AB1.
在 Rt△AD1B1 中,由∠AD1B1 = 30°,
得
tan∠AD1B1 =
=
A
B
B1
C
D
C1
D1
30°
45°
即
解方程,得 x = 25( + 1)≈ 68.
∴ AB = AB1 + BB1
≈ 68 + 1 = 69(m)
答:电视塔的高度为 69 m.
例2 如图一船以 20 n mile/h 的速度向东航行,在 A处测得灯塔 C 在北偏东 60°的方向上,继续航行 1 h 到达B 处,再测得灯塔 C 在北偏东30°的方向上. 已知灯塔 C 四周 10 n mile 内有暗礁,问这船继续向东航行是否安全?
东
北
A
B
30°
60°
C
取决于灯塔 C 到 AB航线的距离是否大于 10 n mile.
东
北
A
B
D
30°
60°
C
解 过点 C 作 CD⊥AB 于点 D,设 CD = x n mile.
在 Rt△ACD 中,AD = =
在 Rt△BCD 中,
BD = =
东
北
A
B
D
30°
60°
C
由 AB = AD – BD,得
AB = – = 20,
解方程,得 x = > 10.
答:这船继续向东航行时安全的.
例3 在 Rt△ABC 中,∠C = 90°,∠B = 42°6′,c = 287.4,解这个直角三角形(精确到 0.1).
解 由 cos B = ,得
a
c
a = c cos B
= 287.4×0.742 0 ≈ 213.3.
由 sin B = ,得
b
c
b = c sin B
= 287.4×0.670 4 ≈ 192.7.
∠A = 90°– 42°6′ = 47°54′.
谈谈你的收获
2.5 三角函数的应用
1、了解仰角、俯角的概念,能应用解直角三角形解决一类观测实际问题
2、进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角
3.知道直线的斜率与直线和x轴正方向所夹的锐角的正切之间的关系。
4.能综合运用解直角三角形的有关知识解决实际问题。
5.经历探索与梯形、坡比等有关的问题的解法,培养学以致用的意识,和数学建模思想。
重点:了解仰角、俯角的概念,能应用解直角三角形解决一类观测实际问题
难点:进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角
A
C
B
a
b
c
复习三角形的三角函数
sin A = ,sin B = ,
cos A = ,cos B = ,
tan A = ,tan B = .
a
c
a
b
b
c
b
a
b
c
a
c
A
C
B
a
b
c
如图,Rt△ABC 共有六个元素,其中∠C = 90°,那么其余五个元素之间有怎样的关系呢?
三条边,三个角
三边 a,b,c,两锐角 A,B
A
C
B
a
b
c
(1)三边之间的关系
a2 + b2 = ____;
(2)锐角之间的关系
∠A + ∠B = ____;
(3)边角之间的关系
sin A = ____,cos A = ____,tan A = ____.
c2
90°
a
c
b
c
a
b
对于锐角 B,也有类似的边角关系吗?
有了以上关系,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
例1 解决本章引言所提问题. 如图,某校九年级学生要测量当地电视塔的高度 AB,因为不能直接到达塔底 B 处,他们采用在发射台院外与电视塔底 B 成一直线的 CD 两处地面上,
A
B
B1
C
D
C1
D1
30°
45°
用测角器测得电视塔顶部 A 的仰角分别为 45°和 30°,同时量得 CD 为 50 m. 已知测角器高为 1 m,问电视塔的高度为多少米?(精确到 1 m)
A
B
B1
C
D
C1
D1
30°
45°
A
B
B1
C
D
C1
D1
30°
45°
解 设 AB1 = x m.
在 Rt△AC1B1 中,由∠AC1B1 = 45°,得
C1B1 = AB1.
在 Rt△AD1B1 中,由∠AD1B1 = 30°,
得
tan∠AD1B1 =
=
A
B
B1
C
D
C1
D1
30°
45°
即
解方程,得 x = 25( + 1)≈ 68.
∴ AB = AB1 + BB1
≈ 68 + 1 = 69(m)
答:电视塔的高度为 69 m.
例2 如图一船以 20 n mile/h 的速度向东航行,在 A处测得灯塔 C 在北偏东 60°的方向上,继续航行 1 h 到达B 处,再测得灯塔 C 在北偏东30°的方向上. 已知灯塔 C 四周 10 n mile 内有暗礁,问这船继续向东航行是否安全?
东
北
A
B
30°
60°
C
取决于灯塔 C 到 AB航线的距离是否大于 10 n mile.
东
北
A
B
D
30°
60°
C
解 过点 C 作 CD⊥AB 于点 D,设 CD = x n mile.
在 Rt△ACD 中,AD = =
在 Rt△BCD 中,
BD = =
东
北
A
B
D
30°
60°
C
由 AB = AD – BD,得
AB = – = 20,
解方程,得 x = > 10.
答:这船继续向东航行时安全的.
例3 在 Rt△ABC 中,∠C = 90°,∠B = 42°6′,c = 287.4,解这个直角三角形(精确到 0.1).
解 由 cos B = ,得
a
c
a = c cos B
= 287.4×0.742 0 ≈ 213.3.
由 sin B = ,得
b
c
b = c sin B
= 287.4×0.670 4 ≈ 192.7.
∠A = 90°– 42°6′ = 47°54′.
谈谈你的收获
