2.6 利用三角函数测高 课件(共16张PPT)
文档属性
| 名称 | 2.6 利用三角函数测高 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 306.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
2.6 利用三角函数测高
教学目标
1、能够设计测量方案、说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题.
2、能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.
3、能够主动积极地想办法,积极地投入到数学活动中去,提高学习数学的兴趣;培养不怕困难的品质,发展合作意识和科学精神.
教学难点
重点:综合运用直角三角形边角关系的知识解决实际问题.
难点:综合运用直角三角形边角关系的知识解决实际问题.
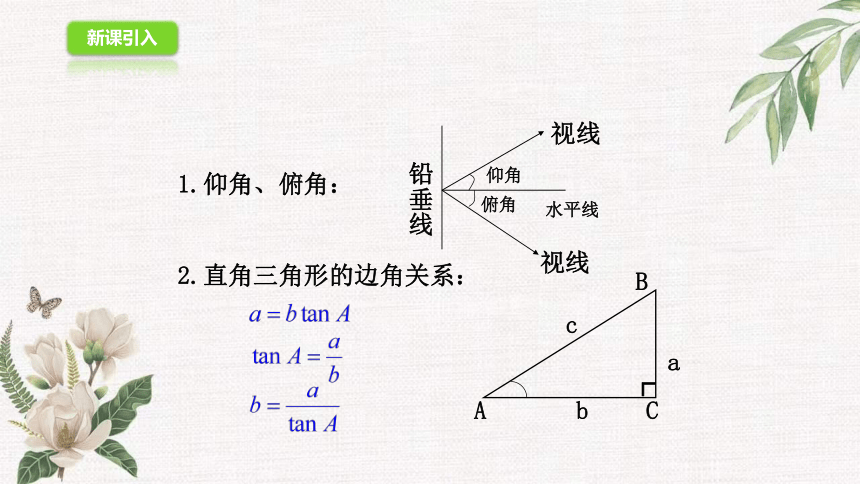
1.仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
b
A
B
C
a
┌
c
2.直角三角形的边角关系:
新课引入
0
30
30
60
60
90
90
P
Q
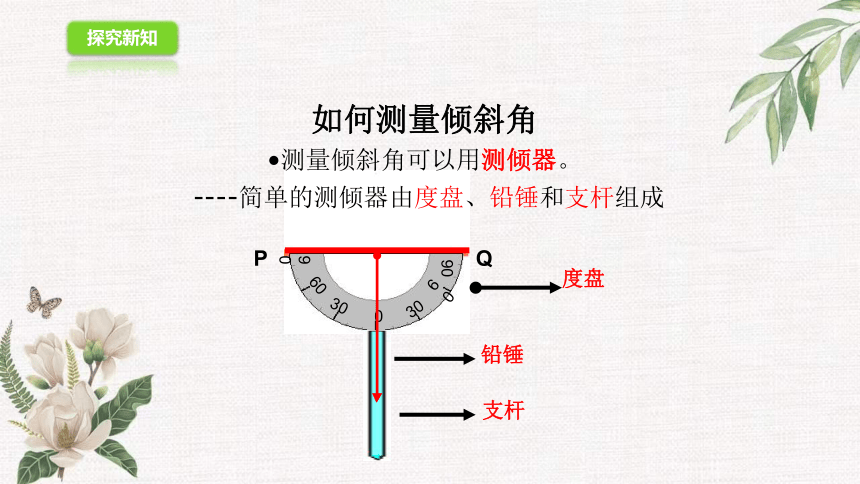
度盘
铅锤
支杆
如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的测倾器由度盘、铅锤和支杆组成
探究新知
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
0
30
30
60
60
90
90
M
30°
P
Q
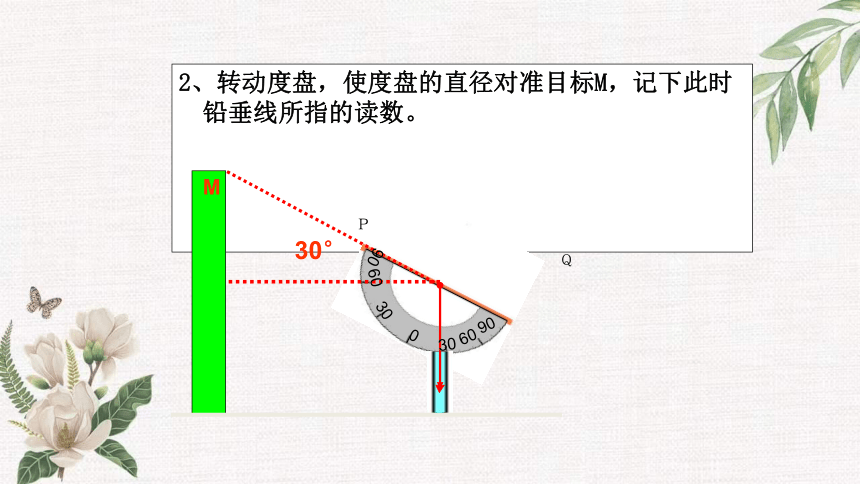
2、转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数。
M
30°
0
30
30
60
60
90
90
P
Q
二、测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
C
A
E
N
M
可按下列步骤进行:
根据刚才测量的数据,你能求出物体MN的高度吗?说说你的理由.
和同伴交流一下你的发现.
在Rt△MCE中,
ME=EC·tanα=AN·tanα
=l·tanα
MN=ME+EN=ME+AC=l·tanα+ a
a
C
A
E
N
M
l
α
议一议
三、测量底部不可以直接到达的物体的高度
所谓“底部不可以到达”---就是在地面上不可以直接测得测点与被测物体之间的距离。
A
C
B
D
M
N
E
α
β
如图,要测量物体MN的高度,可按下列步骤进行:
A
C
B
D
M
N
E
α
β
1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2、在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度。
例 如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
典例精析
在Rt△ MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
过程:根据测量数据,物体MN的高度计算过程为:
a
b
α
E
C
A
D
B
β
N
M
1.如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线,
则tan B的值为__________.
B
A
M
C
巩固练习
2. 一个钢球沿坡角31°的斜坡向上滚动了5米,此时钢球距地面的高度是( )米
A. B. C.
3.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为 ,坡面 的水平宽度为 ,基面AD宽为 2m,则AE= , ,
BC= .
A
D
C
F
E
B
本课主要学习测量物体的高度的方法:
1.测量底部可以到达的物体的高度.
2.测量底部不可以到达的物体的高度.
3.目前我们学习的测量物体高度的方法有相似法、全等法、三角函数法.
课堂小结
2.6 利用三角函数测高
教学目标
1、能够设计测量方案、说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题.
2、能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果.
3、能够主动积极地想办法,积极地投入到数学活动中去,提高学习数学的兴趣;培养不怕困难的品质,发展合作意识和科学精神.
教学难点
重点:综合运用直角三角形边角关系的知识解决实际问题.
难点:综合运用直角三角形边角关系的知识解决实际问题.
1.仰角、俯角:
铅垂线
仰角
俯角
水平线
视线
视线
b
A
B
C
a
┌
c
2.直角三角形的边角关系:
新课引入
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
如何测量倾斜角
测量倾斜角可以用测倾器。
----简单的测倾器由度盘、铅锤和支杆组成
探究新知
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
0
30
30
60
60
90
90
M
30°
P
Q
2、转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数。
M
30°
0
30
30
60
60
90
90
P
Q
二、测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
1.在测点A处安置测倾器,
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
C
A
E
N
M
可按下列步骤进行:
根据刚才测量的数据,你能求出物体MN的高度吗?说说你的理由.
和同伴交流一下你的发现.
在Rt△MCE中,
ME=EC·tanα=AN·tanα
=l·tanα
MN=ME+EN=ME+AC=l·tanα+ a
a
C
A
E
N
M
l
α
议一议
三、测量底部不可以直接到达的物体的高度
所谓“底部不可以到达”---就是在地面上不可以直接测得测点与被测物体之间的距离。
A
C
B
D
M
N
E
α
β
如图,要测量物体MN的高度,可按下列步骤进行:
A
C
B
D
M
N
E
α
β
1、在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2、在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度。
例 如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得), 测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
典例精析
在Rt△ MDE中,
ED=
在Rt△MCE中,
EC =
EC-ED= - =b
过程:根据测量数据,物体MN的高度计算过程为:
a
b
α
E
C
A
D
B
β
N
M
1.如图,在Rt△ABC中,∠C=90°, AM是BC边上的中线,
则tan B的值为__________.
B
A
M
C
巩固练习
2. 一个钢球沿坡角31°的斜坡向上滚动了5米,此时钢球距地面的高度是( )米
A. B. C.
3.如图所示,铁路的路基横断面是等腰梯形,斜坡的坡度为 ,坡面 的水平宽度为 ,基面AD宽为 2m,则AE= , ,
BC= .
A
D
C
F
E
B
本课主要学习测量物体的高度的方法:
1.测量底部可以到达的物体的高度.
2.测量底部不可以到达的物体的高度.
3.目前我们学习的测量物体高度的方法有相似法、全等法、三角函数法.
课堂小结
