数学人教A版(2019)选择性必修第一册 3.1.2椭圆的几何性质-弦长探究 课件(共30张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册 3.1.2椭圆的几何性质-弦长探究 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 807.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 09:48:26 | ||
图片预览








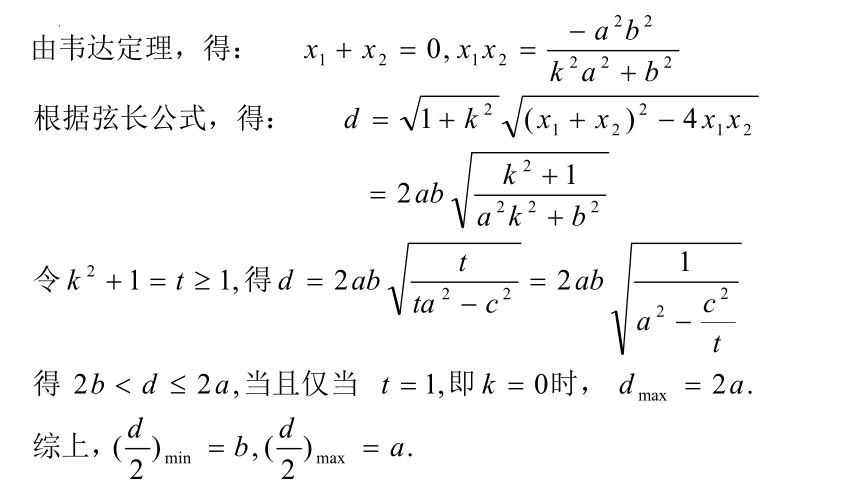

文档简介
(共30张PPT)
3.1.2 椭圆几何性质探究
—弦长
素 养 目 标 学 科 素 养
1.根据弦长公式,能够求出过特殊点的直线与椭圆所截的弦长.(重点) 2.能够熟练运用点差法,计算与中点弦相关的问题. 3.通过对椭圆中弦长问题的探究,让学生进一步体会分类讨论、类比、从特殊到一般的数学思想.(重点、难点) 1、直观想象
2、数学运算
3、逻辑推理
学习目标
焦点位置 x轴 y轴
方程
图形
范围
对称性
顶点
离心率
复习:椭圆的简单几何性质:
F1
F2
M
x
y
O
B2
B1
A1
A2
F1
F2
M
x
y
O
B2
B1
A1
A2
1.什么是椭圆的通径?
2.椭圆的第二定义是什么?
3.直线与椭圆相交的弦长公式?
温故知新
如图示,若直线l与椭圆交于A, B两点,将直线方程与椭圆方程联立消元,得到关于x(或y)的一元二次方程,然后运用两点间距离公式及根与系数的关系,即可求弦长,具体公式为:
其中k为直线l的斜率, a是方程组消元后的一元二次方程的二次项系数, 是判别式.
弦长公式:
O
x
y
F2
l
F1
A
B
Exploration
2
探究2. 椭圆第二定义的相关结论
探究3. 中点弦问题
3
探究1. 椭圆上的点到中心的最短(最长)距离
1
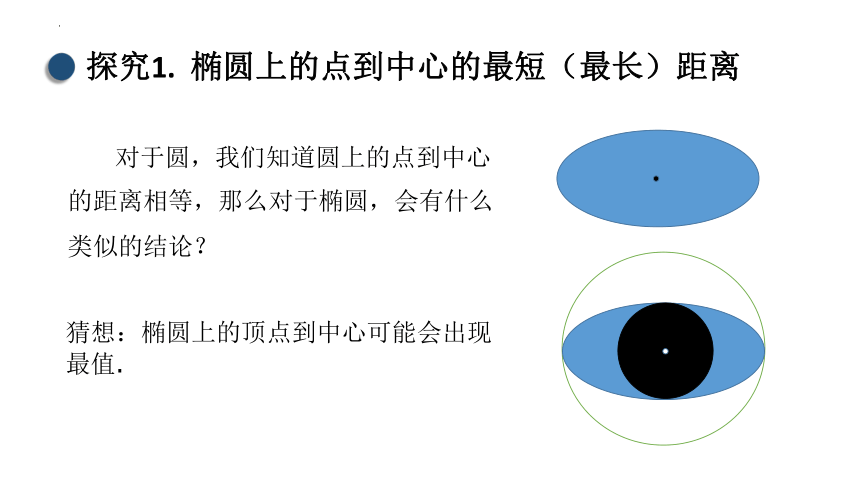
探究1. 椭圆上的点到中心的最短(最长)距离
对于圆,我们知道圆上的点到中心的距离相等,那么对于椭圆,会有什么类似的结论?
猜想:椭圆上的顶点到中心可能会出现最值.
对于焦点在x轴上的椭圆方程 ,
为了表示椭圆上的点,类比圆心在原点的圆的参数方程,
我们可以得到其所对应的的参数方程:
法一:设椭圆上点A的坐标 ,椭圆中心O坐标(0,0),根据平面上两点之间的距离公式,可得:
拓展:若直线的斜率一定,则当直线过椭圆的中心时,弦长最大.
小结:
(1)椭圆上到中心距离最小的点是短轴的两个端点(最小值为短半轴长 ),到中心距离最大的点是长轴的两个端点(最大值为长半轴长 ).
(2)根据椭圆的对称性,可得:过椭圆中心的所有弦长中,最短弦长为 ,最长弦长为 .
探究2. 椭圆第二定义的相关结论
例1 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数 求动点M的轨迹.(特殊情形)
解:
O
x
y
M
H
F
l
d
所以点M 的轨迹是长轴长、短轴长为10、6的椭圆.
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.(一般情形)
O
x
y
M
H
F
l
d
l′
F′
椭圆的第二定义:(课本117页)
即点M 的轨迹是长轴长、短轴长分别为 的椭圆.
椭圆的第二定义:(课本117页)
O
x
y
M
H
F
l
d
l′
F′
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
证明:
说明:|PF1|, |PF2|称为椭圆的焦半径,此公式称为焦半径公式 .
焦半径公式:
y
x
F2
F1
O
P
焦半径公式:
y
x
F2
F1
O
P
y
x
F2
F1
O
M
近日点距离
远日点距离
变式 1(高考题)把椭圆 的长轴AB分成8等分, 过每个分点作x轴的垂线, 交椭圆的上半部于P1、P2、... P7七个点, F是椭圆的一个焦点, 则
|P1F| + |P2F| + · · · + |P7F| = _________.
O
x
y
F
P1
B
A
P2
P3
P4
P6
P5
P7
解1:
解2:
F′
B
变式2 某月球探测器发射后顺利进入了以月球求新为一个焦点的椭圆形轨道,近月点与月球表面的距离为100km,远月点与月球表面的距离为400km.已知月球的直径为3476km,则该椭圆轨道的离心率约为( )
B
过椭圆焦点的弦长问题:
综上可得:对于过焦点的直线,当直线的斜率不存在时,最短弦长为通径 ;当直线的斜率为 0 时,最长弦长为长轴长 ,其余的焦点弦的长度介于两者之间.
小结:
例2 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
探究3 中点弦问题 : (点差法)
O
x
y
F2
l
F1
P
B
A
例3 过椭圆 内一点 引一条弦,使弦被P点平分,则这条弦所在直线l的方程为__________________.
解:
变式3 (新课标全国卷Ⅰ) 已知椭圆E: 的右焦点为F(3,0), 过点F的直线交E于A, B两点. 若AB的中点坐标为(1,-1), 则E的方程为 ( )
D
1. 通径: 若过椭圆 的其中一个焦点垂直于焦点所在坐标轴的直线与椭圆交于P, Q两点, 则| PQ|叫做椭圆的通径, 且
课堂小结:
2. 弦长公式: 若直线 与椭圆 交于A(x1, y1), B(x2, y2)两点, 则
3.椭圆的第二定义以及焦半径公式:
5. 中点弦斜率公式: 若直线 与椭圆 交于A(x1, y1), B(x2, y2)两点, 且AB的中点为M(x0, y0), 则
课堂小结:
4.最值:椭圆上的点到中心最小距离 ,最大距离 ;
过焦点的直线中,最短弦长为通径 ;最长弦长为长轴长
作业
1.习题3.1 复习巩固 5,6,7
2.总结
3.1.2 椭圆几何性质探究
—弦长
素 养 目 标 学 科 素 养
1.根据弦长公式,能够求出过特殊点的直线与椭圆所截的弦长.(重点) 2.能够熟练运用点差法,计算与中点弦相关的问题. 3.通过对椭圆中弦长问题的探究,让学生进一步体会分类讨论、类比、从特殊到一般的数学思想.(重点、难点) 1、直观想象
2、数学运算
3、逻辑推理
学习目标
焦点位置 x轴 y轴
方程
图形
范围
对称性
顶点
离心率
复习:椭圆的简单几何性质:
F1
F2
M
x
y
O
B2
B1
A1
A2
F1
F2
M
x
y
O
B2
B1
A1
A2
1.什么是椭圆的通径?
2.椭圆的第二定义是什么?
3.直线与椭圆相交的弦长公式?
温故知新
如图示,若直线l与椭圆交于A, B两点,将直线方程与椭圆方程联立消元,得到关于x(或y)的一元二次方程,然后运用两点间距离公式及根与系数的关系,即可求弦长,具体公式为:
其中k为直线l的斜率, a是方程组消元后的一元二次方程的二次项系数, 是判别式.
弦长公式:
O
x
y
F2
l
F1
A
B
Exploration
2
探究2. 椭圆第二定义的相关结论
探究3. 中点弦问题
3
探究1. 椭圆上的点到中心的最短(最长)距离
1
探究1. 椭圆上的点到中心的最短(最长)距离
对于圆,我们知道圆上的点到中心的距离相等,那么对于椭圆,会有什么类似的结论?
猜想:椭圆上的顶点到中心可能会出现最值.
对于焦点在x轴上的椭圆方程 ,
为了表示椭圆上的点,类比圆心在原点的圆的参数方程,
我们可以得到其所对应的的参数方程:
法一:设椭圆上点A的坐标 ,椭圆中心O坐标(0,0),根据平面上两点之间的距离公式,可得:
拓展:若直线的斜率一定,则当直线过椭圆的中心时,弦长最大.
小结:
(1)椭圆上到中心距离最小的点是短轴的两个端点(最小值为短半轴长 ),到中心距离最大的点是长轴的两个端点(最大值为长半轴长 ).
(2)根据椭圆的对称性,可得:过椭圆中心的所有弦长中,最短弦长为 ,最长弦长为 .
探究2. 椭圆第二定义的相关结论
例1 动点M(x, y)与定点F(4, 0)的距离和M到定直线l : 的距离的比是常数 求动点M的轨迹.(特殊情形)
解:
O
x
y
M
H
F
l
d
所以点M 的轨迹是长轴长、短轴长为10、6的椭圆.
证明:
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.(一般情形)
O
x
y
M
H
F
l
d
l′
F′
椭圆的第二定义:(课本117页)
即点M 的轨迹是长轴长、短轴长分别为 的椭圆.
椭圆的第二定义:(课本117页)
O
x
y
M
H
F
l
d
l′
F′
平面内的动点M(x, y)到定点F(c, 0)的距离与它到定直线 的距离的比是常数 则点M的轨迹是椭圆.
其中,定点F(c,0)是椭圆的焦点;
定直线 叫做椭圆的准线;
常数 是椭圆的离心率.
证明:
说明:|PF1|, |PF2|称为椭圆的焦半径,此公式称为焦半径公式 .
焦半径公式:
y
x
F2
F1
O
P
焦半径公式:
y
x
F2
F1
O
P
y
x
F2
F1
O
M
近日点距离
远日点距离
变式 1(高考题)把椭圆 的长轴AB分成8等分, 过每个分点作x轴的垂线, 交椭圆的上半部于P1、P2、... P7七个点, F是椭圆的一个焦点, 则
|P1F| + |P2F| + · · · + |P7F| = _________.
O
x
y
F
P1
B
A
P2
P3
P4
P6
P5
P7
解1:
解2:
F′
B
变式2 某月球探测器发射后顺利进入了以月球求新为一个焦点的椭圆形轨道,近月点与月球表面的距离为100km,远月点与月球表面的距离为400km.已知月球的直径为3476km,则该椭圆轨道的离心率约为( )
B
过椭圆焦点的弦长问题:
综上可得:对于过焦点的直线,当直线的斜率不存在时,最短弦长为通径 ;当直线的斜率为 0 时,最长弦长为长轴长 ,其余的焦点弦的长度介于两者之间.
小结:
例2 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
探究3 中点弦问题 : (点差法)
O
x
y
F2
l
F1
P
B
A
例3 过椭圆 内一点 引一条弦,使弦被P点平分,则这条弦所在直线l的方程为__________________.
解:
变式3 (新课标全国卷Ⅰ) 已知椭圆E: 的右焦点为F(3,0), 过点F的直线交E于A, B两点. 若AB的中点坐标为(1,-1), 则E的方程为 ( )
D
1. 通径: 若过椭圆 的其中一个焦点垂直于焦点所在坐标轴的直线与椭圆交于P, Q两点, 则| PQ|叫做椭圆的通径, 且
课堂小结:
2. 弦长公式: 若直线 与椭圆 交于A(x1, y1), B(x2, y2)两点, 则
3.椭圆的第二定义以及焦半径公式:
5. 中点弦斜率公式: 若直线 与椭圆 交于A(x1, y1), B(x2, y2)两点, 且AB的中点为M(x0, y0), 则
课堂小结:
4.最值:椭圆上的点到中心最小距离 ,最大距离 ;
过焦点的直线中,最短弦长为通径 ;最长弦长为长轴长
作业
1.习题3.1 复习巩固 5,6,7
2.总结
