人教A版(2019)高中数学必修第一册 4.4 对数函数课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册 4.4 对数函数课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:25:40 | ||
图片预览











文档简介
(共37张PPT)
4.4 对数函数
第四章 指数函数与对数函数
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
对数
指数幂的运算性质
指数幂及其运算
对数的运算性质
换底公式
二、知识讲解
在 4.2 节中,我们用指数函数模型研究了呈指数增长或衰减变化规律的问题.对这样的问题,在引入对数后,我们还可以从另外的角度,对其蕴含的规律作进一步的研究.
二、知识讲解
4.4.1 对数函数的概念
在 4.2.1 的问题 2 中,我们已经研究了死亡生物体内碳 14 的含量 y 随死亡时间 x 的变化而衰减的规律.反过来,已知死亡生物体内碳 14 的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间 x 是碳 14 的含量 y 的函数吗?
?
思考
二、知识讲解
y
x
1
O
y0
(x0,y0)
图 4.4-1
二、知识讲解
二、知识讲解
例1 求下列函数的定义域:
(1)y=log3 x2;
(2)y=loga (4-x) (a>0,且 a≠1).
解:(1)因为 x2>0,即 x≠0,所以函数 y=log3 x2 的定义域是
{x | x≠0}.
(2)因为 4-x>0,即 x<4,所以函数 y=loga (4-x) 的定义域是
{x | x<4}.
二、知识讲解
例2 假设某地初始物价为 1,每年以 5% 的增长率递增,经过 y 年后的物价为 x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价 x
年数 y
2
1
3
4
5
6
7
8
9
10
0
二、知识讲解
解:(1)由题意可知,经过 y 年后物价 x 为 x=(1+5%)y,即 x=1.05y (y∈ [0,+∞)).由对数与指数间的关系,可得 y=log1.05 x,x∈[1,+∞).由计算工具可得,当 x=2 时,y≈14.所以,该地区的物价大约经过 14 年后会翻一番.
(2)根据函数 y=log1.05 x,x∈[1,+∞),利用计算工具,可得下表:
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加 1 倍所需要的时间在逐渐缩小.
物价 x
年数 y
2
1
3
4
5
6
7
8
9
10
0
23
14
28
33
37
40
43
45
47
二、知识讲解
4.4.2 对数函数的图象和性质
与研究指数函数一样,我们首先画出其图象,然后借助图象研究其性质.
不妨先画函数 y=log2 x 的图象.
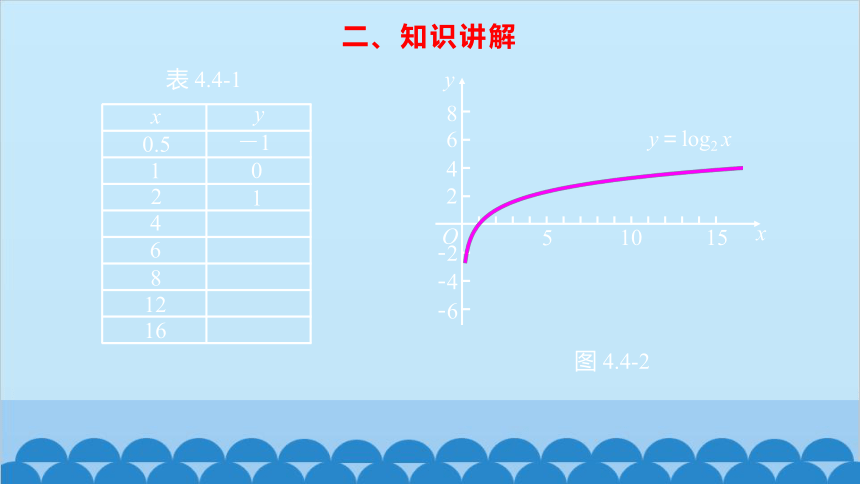
请同学们完成 x,y 的对应值表 4.4-1,并用描点法画出函数 y=log2 x 的图象(图 4.4-2).
二、知识讲解
x
y
8
-1
1
4
0.5
0
1
12
2
6
16
表 4.4-1
x
y
O
图 4.4-2
-6
-2
-4
5
10
15
2
4
y=log2 x
6
8
二、知识讲解
?
思考
二、知识讲解
为了得到对数函数 y=loga x (a>0,且 a≠1) 的性质,我们还需要画出更多具体对数函数的图象进行观察.
y
x
O
log2 x
P
P1
1
图 4.4-3
二、知识讲解
选取底数 a (a>0,且 a≠1) 的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出对数函数 y=loga x (a>0,且 a≠1) 的值域和性质吗?
探究
二、知识讲解
如图 4.4-4,选取底数 a 的若干值,用计算工具画图,发现对数函数 y=loga x 的图象按底数 a 的取值,可分为 01 两种类型.因此,对数函数的性质也可以分 01 两种情况进行研究.
y
x
O
y=log2 x
1
图 4.4-4
y=log3 x
y=log4 x
二、知识讲解
一般地,对数函数的图象和性质如表 4.4-2 所示.
x
y
O
x=1
y=loga x
(1,0)
定义域
图象
值域
性质
(2)减函数
(1)过定点 (1,0),即 x=1 时,y=0
(2)增函数
(0,+∞)
R
0a>1
表 4.4-2
x
y
O
x=1
y=loga x
(1,0)
二、知识讲解
例3 比较下列各题中两个值的大小:
(1)log2 3.4,log2 8.5;
(2)log0.3 1.8,log0.3 2.7;
(3)loga 5.1,loga 5.9 (a>0,且 a≠1).
解:(1) log2 3.4 和 log2 8.5 可看作函数 y=log2 x 的两个函数值.因为底数2>1,对数函数 y=log2 x 是增函数,且 3.4<8.5,所以 log2 3.4(2)log0.3 1.8 和 log0.3 2.7 可看作函数 y=log0.3 x 的两个函数值.因为底数0.3<1,对数函数 y=log0.3 x 是减函数,且 1.8<2.7,所以 log0.3 1.8>log0.3 2.7.
二、知识讲解
例3 比较下列各题中两个值的大小:
(1)log2 3.4,log2 8.5;
(2)log0.3 1.8,log0.3 2.7;
(3)loga 5.1,loga 5.9 (a>0,且 a≠1).
解:(3) loga 5.1 和 loga 5.9 可看作函数 y=loga x 的两个函数值.对数函数的单调性取决于底数 a 是大于 1 还是小于 1,因此需要对底数 a 进行讨论.
当 a>1 时,因为函数 y=loga x 是增函数,且 5.1<5.9,所以 loga 5.1 当 0 loga 5.9.
二、知识讲解
例4 溶液酸碱度的测量.
溶液酸碱度是通过 pH 计算的.pH 的计算公式为 pH=-lg [H+],其中[H+] 表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述 pH 的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为 [H+]=10-7 摩尔/升,计算纯净水的 pH.
二、知识讲解
胃酸中氢离子的浓度是 2.5×10-2 摩尔/升,胃酸的pH 是多少?
?
二、知识讲解
二、知识讲解
二、知识讲解
一般地,指数函数 y=ax (a>0,且 a≠1) 与对数函数 y=loga x (a>0,且 a≠1) 互为反函数,它们的定义域与值域正好互换.
对于指数函数 y=2x,你能利用指数与对数间的关系,得到与之对应的对数函数吗?它们的定义域、值域之间有什么关系?它们也互为反函数吗?
探究
二、知识讲解
4.4.3 不同函数增长的差异
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
选取适当的指数函数与一次函数,探索它们在区间 [0,+∞) 上的增长差异,你能描述一下指数函数增长的特点吗?
探究
二、知识讲解
不妨以函数 y=2x 和 y=2x 为例.
利用信息技术,列出上述两个函数的自变量与函数值的对应值表(表 4.4-3),并在同一直角坐标系中画出它们的图象(图 4.4-5).
x
y=2x
2.5
1
2
1.5
0
1.414
0.5
3
1
2
表 4.4-3
y=2x
2.828
4
5.657
8
0
1
2
3
4
5
6
x
y
O
图 4.4-5
3
1
5
1
2
3
2
4
y=2x
6
8
y=2x
7
二、知识讲解
下面在更大的范围内,观察 y=2x 和 y=2x 的增长情况.
从表 4.4-4 和图 4.4-6 可以看到,当自变量 x 越来越大时,y=2x 的图象就像与 x 轴垂直一样,2x 的值快速增长;而函数 y=2x 的增长速度依然保持不变,与函数 y=2x 的增长速度相比几乎微不足道.
x
y=2x
10
1
16
6
0
4
2
12
4
8
表 4.4-4
y=2x
64
256
1 024
4 096
0
4
8
12
16
20
24
x
y
O
图 4.4-6
600
200
1 000
5
10
15
400
800
y=2x
y=2x
20
二、知识讲解
选取适当的对数函数与一次函数,探索它们在区间 [0,+∞) 上的增长差异,你能描述一下对数函数增长的特点吗?
探究
二、知识讲解
x
y=lg x
50
不存在
1.301
30
0
1
10
60
20
40
表 4.4-5
1.477
1.602
1.699
1.778
0
1
2
3
4
5
6
x
y
O
图 4.4-7
60
50
3
10
30
40
1
2
y=lg x
20
4
5
6
?
思考
二、知识讲解
类比上述过程,
(1)画出一次函数 y=2x,对数函数 y=lg x 和指数函数 y=2x 的图象,并比较它们的增长差异;
(2)试着概括一次函数 y=kx (k>0),对数函数 y=loga x (a>1) 和指数函数 y=bx (b>1) 的增长差异;
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
探究
三、小结
图象
对数函数
概念
性质
不同函数增长的差异
四、练习
四、练习
3.比较下列各题中两个值的大小:
(1)lg 0.6,lg 0.8;(2)log0.5 6,log0.5 4;(3)logm 5,logm 7.
答案: (1)lg 0.6(3)当 0logm 7;当 m>1 时,logm 54.某地去年的 GDP(国内生产总值)为 3 000 亿元人民币,预计未来 5 年的平均增长率为 6.8%.
(1)设经过 x 年达到的年 GDP 为 y 亿元,试写出未来 5 年内,y 关于 x 的函数解析式;
(2)经过几年该地 GDP 能达到 3 900 亿元人民币?
答案:(1)y=3 000×1.068x,0四、练习
四、练习
5.三个变量 y1,y2,y3 随变量 x 变化的数据如下表:
其中关于 x 呈指数增长的变量是___________.
答案:y2.
y3
y2
5
x
130
30
5
10
90
15
20
30
5
y1
505
1 130
2 005
0
4 505
3 130
1 620
524 880
170 061 120
25
29 160
5
9 447 840
55
80
105
130
155
6.如图,对数函数 y=lg x 的图象与一次函数 y=f (x) 的图象有 A,B 两个公共点.求一次函数 y=f (x) 的解析式.
答案:f (x)=(x-1)lg 2.
四、练习
y
x
O
A
B
y=lg x
y=f (x)
2
谢谢观看
4.4 对数函数
第四章 指数函数与对数函数
目录
二、知识讲解
三、小结
四、练习
一、上节回溯
一、上节回溯
对数
指数幂的运算性质
指数幂及其运算
对数的运算性质
换底公式
二、知识讲解
在 4.2 节中,我们用指数函数模型研究了呈指数增长或衰减变化规律的问题.对这样的问题,在引入对数后,我们还可以从另外的角度,对其蕴含的规律作进一步的研究.
二、知识讲解
4.4.1 对数函数的概念
在 4.2.1 的问题 2 中,我们已经研究了死亡生物体内碳 14 的含量 y 随死亡时间 x 的变化而衰减的规律.反过来,已知死亡生物体内碳 14 的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间 x 是碳 14 的含量 y 的函数吗?
?
思考
二、知识讲解
y
x
1
O
y0
(x0,y0)
图 4.4-1
二、知识讲解
二、知识讲解
例1 求下列函数的定义域:
(1)y=log3 x2;
(2)y=loga (4-x) (a>0,且 a≠1).
解:(1)因为 x2>0,即 x≠0,所以函数 y=log3 x2 的定义域是
{x | x≠0}.
(2)因为 4-x>0,即 x<4,所以函数 y=loga (4-x) 的定义域是
{x | x<4}.
二、知识讲解
例2 假设某地初始物价为 1,每年以 5% 的增长率递增,经过 y 年后的物价为 x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价 x
年数 y
2
1
3
4
5
6
7
8
9
10
0
二、知识讲解
解:(1)由题意可知,经过 y 年后物价 x 为 x=(1+5%)y,即 x=1.05y (y∈ [0,+∞)).由对数与指数间的关系,可得 y=log1.05 x,x∈[1,+∞).由计算工具可得,当 x=2 时,y≈14.所以,该地区的物价大约经过 14 年后会翻一番.
(2)根据函数 y=log1.05 x,x∈[1,+∞),利用计算工具,可得下表:
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约每增加 1 倍所需要的时间在逐渐缩小.
物价 x
年数 y
2
1
3
4
5
6
7
8
9
10
0
23
14
28
33
37
40
43
45
47
二、知识讲解
4.4.2 对数函数的图象和性质
与研究指数函数一样,我们首先画出其图象,然后借助图象研究其性质.
不妨先画函数 y=log2 x 的图象.
请同学们完成 x,y 的对应值表 4.4-1,并用描点法画出函数 y=log2 x 的图象(图 4.4-2).
二、知识讲解
x
y
8
-1
1
4
0.5
0
1
12
2
6
16
表 4.4-1
x
y
O
图 4.4-2
-6
-2
-4
5
10
15
2
4
y=log2 x
6
8
二、知识讲解
?
思考
二、知识讲解
为了得到对数函数 y=loga x (a>0,且 a≠1) 的性质,我们还需要画出更多具体对数函数的图象进行观察.
y
x
O
log2 x
P
P1
1
图 4.4-3
二、知识讲解
选取底数 a (a>0,且 a≠1) 的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出对数函数 y=loga x (a>0,且 a≠1) 的值域和性质吗?
探究
二、知识讲解
如图 4.4-4,选取底数 a 的若干值,用计算工具画图,发现对数函数 y=loga x 的图象按底数 a 的取值,可分为 0
y
x
O
y=log2 x
1
图 4.4-4
y=log3 x
y=log4 x
二、知识讲解
一般地,对数函数的图象和性质如表 4.4-2 所示.
x
y
O
x=1
y=loga x
(1,0)
定义域
图象
值域
性质
(2)减函数
(1)过定点 (1,0),即 x=1 时,y=0
(2)增函数
(0,+∞)
R
0
表 4.4-2
x
y
O
x=1
y=loga x
(1,0)
二、知识讲解
例3 比较下列各题中两个值的大小:
(1)log2 3.4,log2 8.5;
(2)log0.3 1.8,log0.3 2.7;
(3)loga 5.1,loga 5.9 (a>0,且 a≠1).
解:(1) log2 3.4 和 log2 8.5 可看作函数 y=log2 x 的两个函数值.因为底数2>1,对数函数 y=log2 x 是增函数,且 3.4<8.5,所以 log2 3.4
二、知识讲解
例3 比较下列各题中两个值的大小:
(1)log2 3.4,log2 8.5;
(2)log0.3 1.8,log0.3 2.7;
(3)loga 5.1,loga 5.9 (a>0,且 a≠1).
解:(3) loga 5.1 和 loga 5.9 可看作函数 y=loga x 的两个函数值.对数函数的单调性取决于底数 a 是大于 1 还是小于 1,因此需要对底数 a 进行讨论.
当 a>1 时,因为函数 y=loga x 是增函数,且 5.1<5.9,所以 loga 5.1
二、知识讲解
例4 溶液酸碱度的测量.
溶液酸碱度是通过 pH 计算的.pH 的计算公式为 pH=-lg [H+],其中[H+] 表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述 pH 的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为 [H+]=10-7 摩尔/升,计算纯净水的 pH.
二、知识讲解
胃酸中氢离子的浓度是 2.5×10-2 摩尔/升,胃酸的pH 是多少?
?
二、知识讲解
二、知识讲解
二、知识讲解
一般地,指数函数 y=ax (a>0,且 a≠1) 与对数函数 y=loga x (a>0,且 a≠1) 互为反函数,它们的定义域与值域正好互换.
对于指数函数 y=2x,你能利用指数与对数间的关系,得到与之对应的对数函数吗?它们的定义域、值域之间有什么关系?它们也互为反函数吗?
探究
二、知识讲解
4.4.3 不同函数增长的差异
在前面的学习中我们看到,一次函数与指数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反映.因此,如果把握了不同函数增长方式的差异,那么就可以根据现实问题的增长情况,选择合适的函数模型刻画其变化规律.下面就来研究一次函数、指数函数和对数函数增长方式的差异.
选取适当的指数函数与一次函数,探索它们在区间 [0,+∞) 上的增长差异,你能描述一下指数函数增长的特点吗?
探究
二、知识讲解
不妨以函数 y=2x 和 y=2x 为例.
利用信息技术,列出上述两个函数的自变量与函数值的对应值表(表 4.4-3),并在同一直角坐标系中画出它们的图象(图 4.4-5).
x
y=2x
2.5
1
2
1.5
0
1.414
0.5
3
1
2
表 4.4-3
y=2x
2.828
4
5.657
8
0
1
2
3
4
5
6
x
y
O
图 4.4-5
3
1
5
1
2
3
2
4
y=2x
6
8
y=2x
7
二、知识讲解
下面在更大的范围内,观察 y=2x 和 y=2x 的增长情况.
从表 4.4-4 和图 4.4-6 可以看到,当自变量 x 越来越大时,y=2x 的图象就像与 x 轴垂直一样,2x 的值快速增长;而函数 y=2x 的增长速度依然保持不变,与函数 y=2x 的增长速度相比几乎微不足道.
x
y=2x
10
1
16
6
0
4
2
12
4
8
表 4.4-4
y=2x
64
256
1 024
4 096
0
4
8
12
16
20
24
x
y
O
图 4.4-6
600
200
1 000
5
10
15
400
800
y=2x
y=2x
20
二、知识讲解
选取适当的对数函数与一次函数,探索它们在区间 [0,+∞) 上的增长差异,你能描述一下对数函数增长的特点吗?
探究
二、知识讲解
x
y=lg x
50
不存在
1.301
30
0
1
10
60
20
40
表 4.4-5
1.477
1.602
1.699
1.778
0
1
2
3
4
5
6
x
y
O
图 4.4-7
60
50
3
10
30
40
1
2
y=lg x
20
4
5
6
?
思考
二、知识讲解
类比上述过程,
(1)画出一次函数 y=2x,对数函数 y=lg x 和指数函数 y=2x 的图象,并比较它们的增长差异;
(2)试着概括一次函数 y=kx (k>0),对数函数 y=loga x (a>1) 和指数函数 y=bx (b>1) 的增长差异;
(3)讨论交流“直线上升”“对数增长”“指数爆炸”的含义.
探究
三、小结
图象
对数函数
概念
性质
不同函数增长的差异
四、练习
四、练习
3.比较下列各题中两个值的大小:
(1)lg 0.6,lg 0.8;(2)log0.5 6,log0.5 4;(3)logm 5,logm 7.
答案: (1)lg 0.6
(1)设经过 x 年达到的年 GDP 为 y 亿元,试写出未来 5 年内,y 关于 x 的函数解析式;
(2)经过几年该地 GDP 能达到 3 900 亿元人民币?
答案:(1)y=3 000×1.068x,0
四、练习
5.三个变量 y1,y2,y3 随变量 x 变化的数据如下表:
其中关于 x 呈指数增长的变量是___________.
答案:y2.
y3
y2
5
x
130
30
5
10
90
15
20
30
5
y1
505
1 130
2 005
0
4 505
3 130
1 620
524 880
170 061 120
25
29 160
5
9 447 840
55
80
105
130
155
6.如图,对数函数 y=lg x 的图象与一次函数 y=f (x) 的图象有 A,B 两个公共点.求一次函数 y=f (x) 的解析式.
答案:f (x)=(x-1)lg 2.
四、练习
y
x
O
A
B
y=lg x
y=f (x)
2
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
