湘教版七年级数学上册第2章代数式 单元综合测试题(含解析)
文档属性
| 名称 | 湘教版七年级数学上册第2章代数式 单元综合测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 73.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 16:01:28 | ||
图片预览



文档简介
2022-2023学年湘教版七年级数学上册《第2章代数式》单元综合测试题(附答案)
一.选择题(共8小题,满分32分)
1.将代数式a﹣(b﹣c)去括号,得( )
A.a﹣b+c B.﹣a+b﹣c C.a+b+c D.a﹣b﹣c
2.下列各选项中,两个单项式不是同类项的是( )
A.3x2y和 B.1与﹣2
C.m2n和3×102nm2 D.与
3.下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y+z
C.x+2y+2z=x﹣2(y+z)
D.﹣a+c+d﹣b=﹣(a+b)+(c+d)
4.用字母表示数,下列书写规范的是( )
A.2×a×b B.ax÷2 C.a2b D.2ab
5.在x,1,x2﹣2,πr2,,,V=πr2h中,代数式的个数为( )
A.5个 B.4个 C.3个 D.2个
6.用代数式表示“a的2倍与b的差的平方”,正确的是( )
A.2(a﹣b)2 B.2a﹣b2 C.(2a﹣b)2 D.(a﹣2b)2
7.下列叙述正确的是( )
A.5不是代数式
B.一个字母不是代数式
C.x的5倍与y的的差可表示为5x﹣
D.s=πR2是代数式
8.如图,做一个试管架,在acm长的木条上钻4个圆孔,每个孔半径为2cm,则x=( )
A.cm B.cm C.cm D.cm
二.填空题(共8小题,满分32分)
9.单项式﹣2xy2的次数是 .
10.去括号:﹣[﹣(m﹣n)]= .
11.已知a2﹣ab=20,ab﹣b2=﹣12,则a2﹣b2= ,a2﹣2ab+b2= .
12.﹣2xmyn﹣2与3x5y2﹣n是同类项,则m﹣n= .
13.把多项式2x3y4﹣3xy﹣5x4y3+3x2y2﹣y5按x的降幂排列为 .
14.一个三位数,a表示百位数,b表示十位数,c表示个位数,那么这个数可表示为 .
15.若当x=﹣2时,代数式ax5+bx3+cx+2的值为6,则当x=2时,代数式ax5+bx3+cx+2的值是 .
16.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足 .
三.解答题(共8小题,满分56分)
17.化简下列各式:
(1)2a+6b﹣3a﹣b;
(2)m﹣(2m﹣3n)+2(3m﹣5n);
(3);
(4)2x2y﹣[2xy2﹣2(x2y+2xy2)].
18.先化简,再求值.
(1),其中x=﹣2;
(2)(5a2﹣3b2)+(a2+b2)﹣(5a2+3b2),其中a=﹣1,b=1.
19.已知多项式﹣5x2a+1y2﹣x3y3+x4y.
(1)求多项式中各项的系数和次数;
(2)若多项式是7次多项式,求a的值.
20.已知一个多项式与x2﹣xy的3倍的和等于5x2﹣3xy+2y2,求这个多项式.
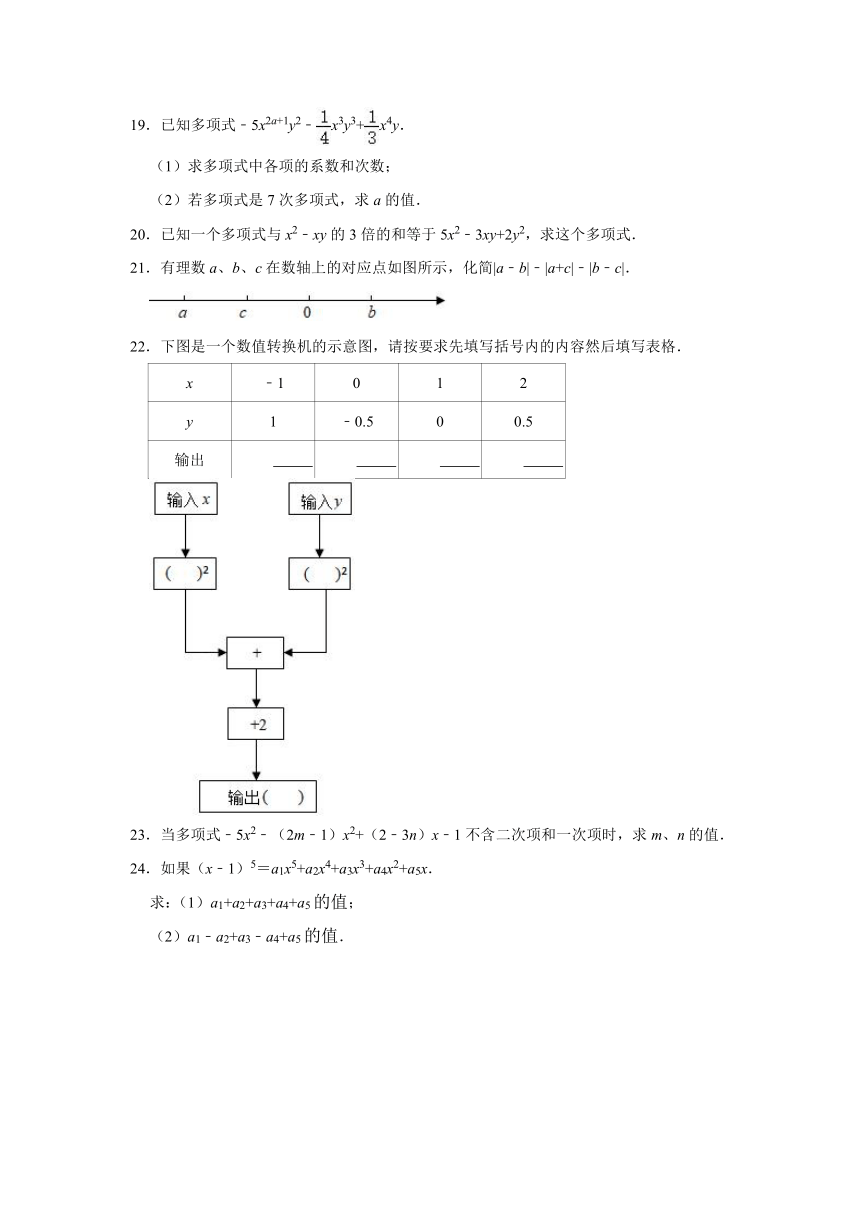
21.有理数a、b、c在数轴上的对应点如图所示,化简|a﹣b|﹣|a+c|﹣|b﹣c|.
22.下图是一个数值转换机的示意图,请按要求先填写括号内的内容然后填写表格.
x ﹣1 0 1 2
y 1 ﹣0.5 0 0.5
输出
23.当多项式﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1不含二次项和一次项时,求m、n的值.
24.如果(x﹣1)5=a1x5+a2x4+a3x3+a4x2+a5x.
求:(1)a1+a2+a3+a4+a5的值;
(2)a1﹣a2+a3﹣a4+a5的值.
参考答案
一.选择题(共8小题,满分32分)
1.解:a﹣(b﹣c)=a﹣b+c.
故选:A.
2.解:A、所含字母相同,并且相同字母的指数也相同,是同类项,故此选项不符合题意;
B、所有常数项都是同类项,故此选项不符合题意;
C、所含字母相同,并且相同字母的指数也相同,是同类项,故此选项不符合题意;
D、所含字母相同,相同字母的指数不相同,不是同类项,故此选项符合题意.
故选:D.
3.解:A、原式=x﹣y+z,不符合题意;
B、原式=﹣x+y﹣z,不符合题意;
C、x+2y+2z=x﹣2(﹣y﹣z),不符合题意;
D、﹣a+c+d﹣b=﹣(a+b)+(c+d),符合题意;
故选:D.
4.解:A、原书写错误,正确的书写格式是2ab,故此选项不符合题意;
B、原书写错误,正确的书写格式是,故此选项不符合题意;
C、原书写错误,正确的书写格式是2ab,故此选项不符合题意;
D、原书写正确,故此选项符合题意.
故选:D.
5.解:在x,1,x2﹣2,πr2,,,V=πr2h中,
代数式有:x,1,x2﹣2,πr2,,共5个,
故选:A.
6.解:依题意得:(2a﹣b)2.
故选:C.
7.解:代数式是用运算符号把数与字母连起来的式子,单个的数或字母也是代数式,代数式不含有关系符号,即不含有=、≠、<、>、≤、≥等符号,
故A、B、D不正确,不符合题意,
x的5倍与y的的差可表示为5x﹣y,故C正确,符合题意,
故选:C.
8.解:依题意有x==(cm).
故选:B.
二.填空题(共8小题,满分32分)
9.解:根据单项式次数的定义,﹣2xy2的次数为1+2=3.
故答案为:3.
10.解:﹣[﹣(m﹣n)]
=﹣(﹣m+n)
=m﹣n.
故答案为:m﹣n.
11.解:∵a2﹣ab=20,ab﹣b2=﹣12,
∴a2﹣b2=a2﹣ab+ab﹣b2=20﹣12=8;a2﹣2ab+b2=a2﹣ab﹣ab+b2=20+12=32.
故答案为:8;32.
12.解:∵﹣2xmyn﹣2与3x5y2﹣n是同类项,
∴m=5,n﹣2=2﹣n,
∴m=5,n=2,
则m﹣n=5﹣2=3.
故答案为:3.
13.解:把多项式2x3y4﹣3xy﹣5x4y3+3x2y2﹣y5按x的降幂排列为﹣5x4y3+2x3y4+3x2y2﹣3xy﹣y5.
故答案为﹣5x4y3+2x3y4+3x2y2﹣3xy﹣y5.
14.解:∵一个三位数,a表示百位数,b表示十位数,c表示个位数,
∴这个数可以表示为:100a+10b+c,
故答案为:100a+10b+c.
15.解:∵当x=﹣2时,代数式ax5+bx3+cx+2的值为6,
∴a×(﹣2)5+b×(﹣2)3+c×(﹣2)+2=6,即﹣32a﹣8b﹣2c=4,
∴32a+8b+2c=﹣4,
当x=2时,
ax5+bx3+cx+2
=a×25+b×23+2c+2
=(32a+8b+2c)+2
=﹣4+2
=﹣2,
故答案为:﹣2.
16.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
故答案为:a=3b.
三.解答题(共8小题,满分56分)
17.解:(1)2a+6b﹣3a﹣b
=(2﹣3)a+(6﹣1)b
=﹣a+5b;
(2)m﹣(2m﹣3n)+2(3m﹣5n)
=m﹣2m+3n+6m﹣10n
=5m﹣7n;
(3)
=x2﹣5x﹣2x2+x
=﹣x2﹣x;
(4)2x2y﹣[2xy2﹣2(x2y+2xy2)]
=2x2y﹣2xy2+2(x2y+2xy2)
=2x2y﹣2xy2+2x2y+4xy2
=4x2y+2xy2.
18.解:(1)原式=9x+6x2﹣3x+2x2
=6x+8x2,
当x=﹣2时,
原式=6×(﹣2)+8×4
=﹣12+32
=20.
(2)原式=5a2﹣3b2+a2+b2﹣5a2﹣3b2
=a2﹣5b2,
当a=﹣1,b=1时,
原式=1﹣5
=﹣4.
19.解:(1)﹣5x2a+1y2的系数是﹣5,次数是2a+3;
﹣x3y3的系数是:,次数是6;
x4y的系数是:,次数是5;
(2)由多项式的次数是7,可知﹣5x2a+1y2的次数是7,即2a+3=7,
解得:a=2.
20.解:∵一个多项式与x2﹣xy的3倍的和等于5x2﹣3xy+2y2,
∴这个多项式为:5x2﹣3xy+2y2﹣3(x2﹣xy)
=5x2﹣3xy+2y2﹣3x2+3xy
=2x2+2y2.
21.解:由图可知,a﹣b<0,a+c<0,b﹣c>0,
|a﹣b|﹣|a+c|﹣|b﹣c|
=﹣(a﹣b)+(a+c)﹣(b﹣c)
=﹣a+b+a+c﹣b+c
=2c.
22.解:当x=﹣1,y=1时,x2+y2+2=1+1+2=4;
当x=0,y=﹣0.5时,x2+y2+2=0+0.25+2=2.25;
当x=1,y=0时,x2+y2+2=1+0+2=3;
当x=2,y=0.5时,x2+y2+2=4+0.25+2=6.25;
故答案为:4,2.25,3,6.25.
23.解:﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1=﹣(2m+4)x2+(2﹣3n)x﹣1,
∵多项式﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1不含二次项和一次项,
∴﹣(2m+4)=0,解得m=﹣2;
2﹣3n=0,解得n=.
故m的值为﹣2、n的值为.
24.解:(1)∵(x﹣1)5=a1x5+a2x4+a3x3+a4x2+a5x,
∴当x=1时,a1+a2+a3+a4+a5=0;
故答案为:0;
(2)当x=﹣1时,﹣a1+a2﹣a3+a4﹣a5=(﹣1﹣1)5=﹣32,
∴a1﹣a2+a3﹣a4+a5=32,
故答案为:32.
一.选择题(共8小题,满分32分)
1.将代数式a﹣(b﹣c)去括号,得( )
A.a﹣b+c B.﹣a+b﹣c C.a+b+c D.a﹣b﹣c
2.下列各选项中,两个单项式不是同类项的是( )
A.3x2y和 B.1与﹣2
C.m2n和3×102nm2 D.与
3.下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y+z
C.x+2y+2z=x﹣2(y+z)
D.﹣a+c+d﹣b=﹣(a+b)+(c+d)
4.用字母表示数,下列书写规范的是( )
A.2×a×b B.ax÷2 C.a2b D.2ab
5.在x,1,x2﹣2,πr2,,,V=πr2h中,代数式的个数为( )
A.5个 B.4个 C.3个 D.2个
6.用代数式表示“a的2倍与b的差的平方”,正确的是( )
A.2(a﹣b)2 B.2a﹣b2 C.(2a﹣b)2 D.(a﹣2b)2
7.下列叙述正确的是( )
A.5不是代数式
B.一个字母不是代数式
C.x的5倍与y的的差可表示为5x﹣
D.s=πR2是代数式
8.如图,做一个试管架,在acm长的木条上钻4个圆孔,每个孔半径为2cm,则x=( )
A.cm B.cm C.cm D.cm
二.填空题(共8小题,满分32分)
9.单项式﹣2xy2的次数是 .
10.去括号:﹣[﹣(m﹣n)]= .
11.已知a2﹣ab=20,ab﹣b2=﹣12,则a2﹣b2= ,a2﹣2ab+b2= .
12.﹣2xmyn﹣2与3x5y2﹣n是同类项,则m﹣n= .
13.把多项式2x3y4﹣3xy﹣5x4y3+3x2y2﹣y5按x的降幂排列为 .
14.一个三位数,a表示百位数,b表示十位数,c表示个位数,那么这个数可表示为 .
15.若当x=﹣2时,代数式ax5+bx3+cx+2的值为6,则当x=2时,代数式ax5+bx3+cx+2的值是 .
16.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足 .
三.解答题(共8小题,满分56分)
17.化简下列各式:
(1)2a+6b﹣3a﹣b;
(2)m﹣(2m﹣3n)+2(3m﹣5n);
(3);
(4)2x2y﹣[2xy2﹣2(x2y+2xy2)].
18.先化简,再求值.
(1),其中x=﹣2;
(2)(5a2﹣3b2)+(a2+b2)﹣(5a2+3b2),其中a=﹣1,b=1.
19.已知多项式﹣5x2a+1y2﹣x3y3+x4y.
(1)求多项式中各项的系数和次数;
(2)若多项式是7次多项式,求a的值.
20.已知一个多项式与x2﹣xy的3倍的和等于5x2﹣3xy+2y2,求这个多项式.
21.有理数a、b、c在数轴上的对应点如图所示,化简|a﹣b|﹣|a+c|﹣|b﹣c|.
22.下图是一个数值转换机的示意图,请按要求先填写括号内的内容然后填写表格.
x ﹣1 0 1 2
y 1 ﹣0.5 0 0.5
输出
23.当多项式﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1不含二次项和一次项时,求m、n的值.
24.如果(x﹣1)5=a1x5+a2x4+a3x3+a4x2+a5x.
求:(1)a1+a2+a3+a4+a5的值;
(2)a1﹣a2+a3﹣a4+a5的值.
参考答案
一.选择题(共8小题,满分32分)
1.解:a﹣(b﹣c)=a﹣b+c.
故选:A.
2.解:A、所含字母相同,并且相同字母的指数也相同,是同类项,故此选项不符合题意;
B、所有常数项都是同类项,故此选项不符合题意;
C、所含字母相同,并且相同字母的指数也相同,是同类项,故此选项不符合题意;
D、所含字母相同,相同字母的指数不相同,不是同类项,故此选项符合题意.
故选:D.
3.解:A、原式=x﹣y+z,不符合题意;
B、原式=﹣x+y﹣z,不符合题意;
C、x+2y+2z=x﹣2(﹣y﹣z),不符合题意;
D、﹣a+c+d﹣b=﹣(a+b)+(c+d),符合题意;
故选:D.
4.解:A、原书写错误,正确的书写格式是2ab,故此选项不符合题意;
B、原书写错误,正确的书写格式是,故此选项不符合题意;
C、原书写错误,正确的书写格式是2ab,故此选项不符合题意;
D、原书写正确,故此选项符合题意.
故选:D.
5.解:在x,1,x2﹣2,πr2,,,V=πr2h中,
代数式有:x,1,x2﹣2,πr2,,共5个,
故选:A.
6.解:依题意得:(2a﹣b)2.
故选:C.
7.解:代数式是用运算符号把数与字母连起来的式子,单个的数或字母也是代数式,代数式不含有关系符号,即不含有=、≠、<、>、≤、≥等符号,
故A、B、D不正确,不符合题意,
x的5倍与y的的差可表示为5x﹣y,故C正确,符合题意,
故选:C.
8.解:依题意有x==(cm).
故选:B.
二.填空题(共8小题,满分32分)
9.解:根据单项式次数的定义,﹣2xy2的次数为1+2=3.
故答案为:3.
10.解:﹣[﹣(m﹣n)]
=﹣(﹣m+n)
=m﹣n.
故答案为:m﹣n.
11.解:∵a2﹣ab=20,ab﹣b2=﹣12,
∴a2﹣b2=a2﹣ab+ab﹣b2=20﹣12=8;a2﹣2ab+b2=a2﹣ab﹣ab+b2=20+12=32.
故答案为:8;32.
12.解:∵﹣2xmyn﹣2与3x5y2﹣n是同类项,
∴m=5,n﹣2=2﹣n,
∴m=5,n=2,
则m﹣n=5﹣2=3.
故答案为:3.
13.解:把多项式2x3y4﹣3xy﹣5x4y3+3x2y2﹣y5按x的降幂排列为﹣5x4y3+2x3y4+3x2y2﹣3xy﹣y5.
故答案为﹣5x4y3+2x3y4+3x2y2﹣3xy﹣y5.
14.解:∵一个三位数,a表示百位数,b表示十位数,c表示个位数,
∴这个数可以表示为:100a+10b+c,
故答案为:100a+10b+c.
15.解:∵当x=﹣2时,代数式ax5+bx3+cx+2的值为6,
∴a×(﹣2)5+b×(﹣2)3+c×(﹣2)+2=6,即﹣32a﹣8b﹣2c=4,
∴32a+8b+2c=﹣4,
当x=2时,
ax5+bx3+cx+2
=a×25+b×23+2c+2
=(32a+8b+2c)+2
=﹣4+2
=﹣2,
故答案为:﹣2.
16.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
故答案为:a=3b.
三.解答题(共8小题,满分56分)
17.解:(1)2a+6b﹣3a﹣b
=(2﹣3)a+(6﹣1)b
=﹣a+5b;
(2)m﹣(2m﹣3n)+2(3m﹣5n)
=m﹣2m+3n+6m﹣10n
=5m﹣7n;
(3)
=x2﹣5x﹣2x2+x
=﹣x2﹣x;
(4)2x2y﹣[2xy2﹣2(x2y+2xy2)]
=2x2y﹣2xy2+2(x2y+2xy2)
=2x2y﹣2xy2+2x2y+4xy2
=4x2y+2xy2.
18.解:(1)原式=9x+6x2﹣3x+2x2
=6x+8x2,
当x=﹣2时,
原式=6×(﹣2)+8×4
=﹣12+32
=20.
(2)原式=5a2﹣3b2+a2+b2﹣5a2﹣3b2
=a2﹣5b2,
当a=﹣1,b=1时,
原式=1﹣5
=﹣4.
19.解:(1)﹣5x2a+1y2的系数是﹣5,次数是2a+3;
﹣x3y3的系数是:,次数是6;
x4y的系数是:,次数是5;
(2)由多项式的次数是7,可知﹣5x2a+1y2的次数是7,即2a+3=7,
解得:a=2.
20.解:∵一个多项式与x2﹣xy的3倍的和等于5x2﹣3xy+2y2,
∴这个多项式为:5x2﹣3xy+2y2﹣3(x2﹣xy)
=5x2﹣3xy+2y2﹣3x2+3xy
=2x2+2y2.
21.解:由图可知,a﹣b<0,a+c<0,b﹣c>0,
|a﹣b|﹣|a+c|﹣|b﹣c|
=﹣(a﹣b)+(a+c)﹣(b﹣c)
=﹣a+b+a+c﹣b+c
=2c.
22.解:当x=﹣1,y=1时,x2+y2+2=1+1+2=4;
当x=0,y=﹣0.5时,x2+y2+2=0+0.25+2=2.25;
当x=1,y=0时,x2+y2+2=1+0+2=3;
当x=2,y=0.5时,x2+y2+2=4+0.25+2=6.25;
故答案为:4,2.25,3,6.25.
23.解:﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1=﹣(2m+4)x2+(2﹣3n)x﹣1,
∵多项式﹣5x2﹣(2m﹣1)x2+(2﹣3n)x﹣1不含二次项和一次项,
∴﹣(2m+4)=0,解得m=﹣2;
2﹣3n=0,解得n=.
故m的值为﹣2、n的值为.
24.解:(1)∵(x﹣1)5=a1x5+a2x4+a3x3+a4x2+a5x,
∴当x=1时,a1+a2+a3+a4+a5=0;
故答案为:0;
(2)当x=﹣1时,﹣a1+a2﹣a3+a4﹣a5=(﹣1﹣1)5=﹣32,
∴a1﹣a2+a3﹣a4+a5=32,
故答案为:32.
同课章节目录
