苏科版七年级数学上册第2章有理数单元综合测试题(含解析)
文档属性
| 名称 | 苏科版七年级数学上册第2章有理数单元综合测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 138.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 15:37:12 | ||
图片预览




文档简介
2022-2023学年苏科版七年级数学上册《第2章有理数》单元综合测试题(附答案)
一.选择题(共8小题,满分32分)
1.如果收入200元记作+200元,那么支出150元记作( )
A.+150元 B.﹣150元 C.+50元 D.﹣50元
2.下列一组数:﹣8,2.7,,,0.66666…,0,2,0.080080008…,其中是无理数的有( )
A.0个 B.1个 C.2个 D.3个
3.在四包真空小包装火腿,每包以标准克数(450克)0为基数,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准的是( )
A.+2 B.﹣3 C.﹣1 D.+4
4.下列各组数中,互为相反数的是( )
A.2与 B.(﹣1)2与1 C.﹣1与(﹣1)3 D.﹣(﹣2)与﹣|﹣2|
5.下列运算正确的是( )
A. B.﹣7﹣2×5=﹣9×5=﹣45
C. D.﹣(﹣3)2=﹣9
6.下列说法正确的是( )
①有理数包括正有理数和负有理数 ②相反数大于本身的数是负数
③数轴上原点两侧的数互为相反数 ④两个数比较,绝对值大的反而小.
A.② B.①③ C.①② D.②③④
7.如果有理数a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是倒数等于它本身的数,那么式子a﹣b+c2﹣|d|的值是( )
A.﹣2 B.﹣1 C.0 D.1
8.把所有正整数从小到大排列,并按如下规律分组:(1),(2,3,4),(5,6,7,8,9),(10,11,12,13,14,15,16),…,现用等式AM=(i,j)表示正整数M是第i组第j个数(从左往右数),如A7=(3,3),则A2020=( )
A.(44,81) B.(44,82) C.(45,83) D.(45,84)
二.填空题(共8小题,满分32分)
9.的相反数是 ,的倒数是 ,+(﹣5)的绝对值为 .
10.平方等于25的数是 .
11.据测算,我国每年因沙漠造成的直接经济损失超过5 400 000万元,这个数用科学记数法表示为 万元.
12.若|a|=1,|b|=4,且a+b<0,则a+b= .
13.绝对值不大于3的所有整数有 .
14.如图所示是计算机某计算程序,若开始输入x=﹣1,则最后输出的结果是 .
15.若(x﹣2)2+|y+3|=0,则yx的值是 .
16.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2023次跳后它停的点所对应的数为 .
三.解答题(共8小题,满分56分)
17.计算
①﹣20+(﹣14)﹣(﹣18)﹣13
②(﹣56)×(﹣+)
③2×(﹣3)2﹣5÷(﹣)×(﹣2)
④﹣9×36(用简便方法)
⑤﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].
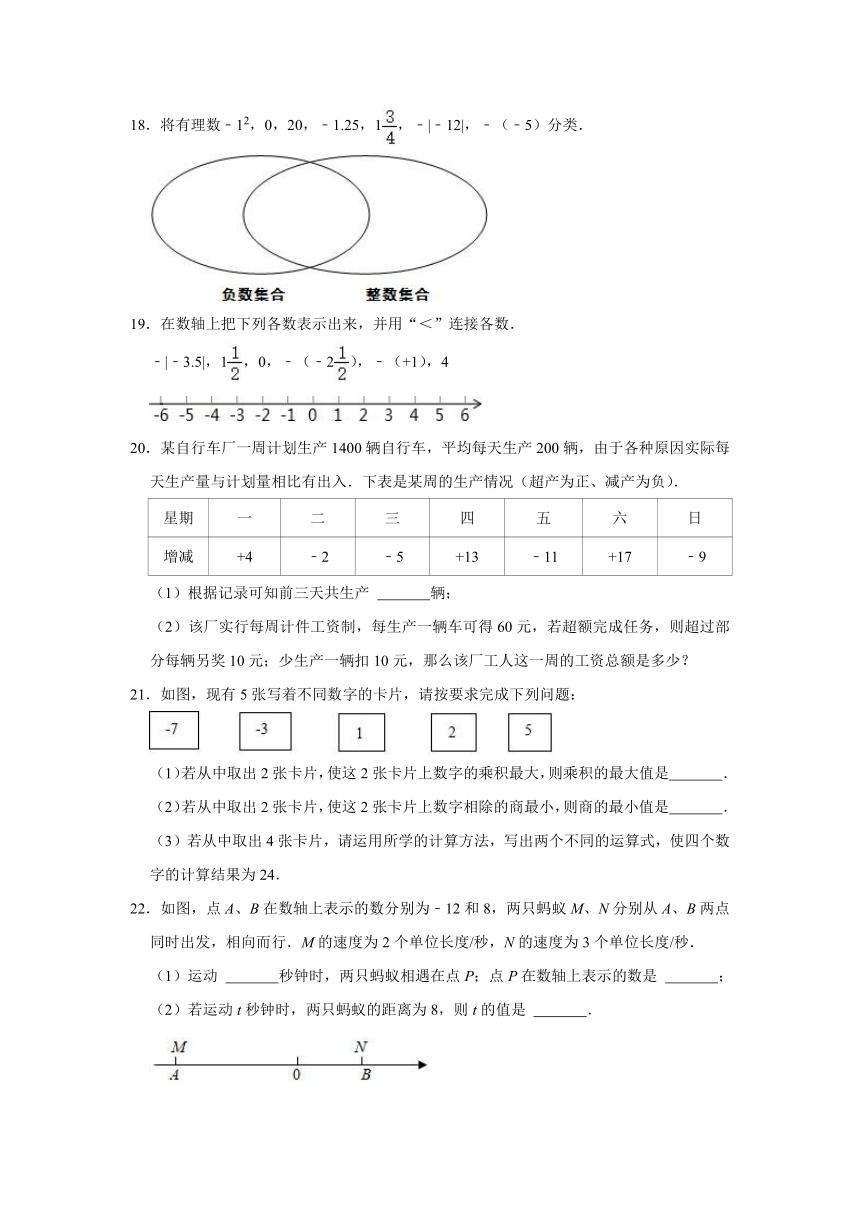
18.将有理数﹣12,0,20,﹣1.25,1,﹣|﹣12|,﹣(﹣5)分类.
19.在数轴上把下列各数表示出来,并用“<”连接各数.
﹣|﹣3.5|,1,0,﹣(﹣2),﹣(+1),4
20.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负).
星期 一 二 三 四 五 六 日
增减 +4 ﹣2 ﹣5 +13 ﹣11 +17 ﹣9
(1)根据记录可知前三天共生产 辆;
(2)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖10元;少生产一辆扣10元,那么该厂工人这一周的工资总额是多少?
21.如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
(1)若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是 .
(2)若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是 .
(3)若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
22.如图,点A、B在数轴上表示的数分别为﹣12和8,两只蚂蚁M、N分别从A、B两点同时出发,相向而行.M的速度为2个单位长度/秒,N的速度为3个单位长度/秒.
(1)运动 秒钟时,两只蚂蚁相遇在点P;点P在数轴上表示的数是 ;
(2)若运动t秒钟时,两只蚂蚁的距离为8,则t的值是 .
23.利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合,请利用数形结合的思想解决下列问题.
(1)如图,一个边长为1的正方形,依次取正方形面积的、、、…、,根据图(1)我们可以知道:+++…+= .
利用上述公式计算:2﹣22﹣23﹣24﹣25﹣26﹣…﹣22021+22022.
(2)如图(2),一个边长为1的正方形,依次取剩余部分的,根据图示计算:+++…+= .
(3)如图(3)是一个边长为1的正方形,根据图示计算:++++…+= .
24.我们知道,|x|表示x在数轴上对应的点到原点的距离我们可以把|x|看作|x﹣0|,所以,|x﹣3|就表示x在数轴上对应的点到3的距离,|x+1|=|x﹣(﹣1)|就表示x在数轴上对应的点到﹣1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求|x﹣4|+|x+2|的最小值,并写出此时x的取值情况;
(2)求|x﹣3|+|x+2|+|x+6|的最小值,并写出此时x的取值情况;
(3)已知|x﹣1|+|x+2|+|y﹣3|+|y+4|=10,求2x+y的最大值和最小值.
参考答案
一.选择题(共8小题,满分32分)
1.解:因为正”和“负”相对,所以,如果收入200元记作+200元,那么支出150元记作﹣150元.
故选:B.
2.解:,0.080080008…是无理数,
故选:C.
3.解:A、+2的绝对值是2;
B、﹣3的绝对值是3;
C、﹣1的绝对值是1;
D、+4的绝对值是4.
C选项的绝对值最小.
故选:C.
4.解:A、2与不是互为相反数,故本选项错误;
B、(﹣1)2与1相等,不是互为相反数,故本选项错误;
C、﹣1与(﹣1)3相等,不是互为相反数,故本选项错误;
D、﹣(﹣2)=2,﹣|﹣2|=﹣2,是互为相反数,故本选项正确.
故选:D.
5.解:A、,故选项错误;
B、﹣7﹣2×5=﹣7﹣10=﹣17,故选项错误;
C、,故选项错误;
D、﹣(﹣3)2=﹣9,故选项正确.
故选:D.
6.解:①有理数包括正有理数,负有理数和0,原来的说法不正确.
②说法正确.
③数轴上原点两侧的数不一定互为相反数,原来的说法不正确.
④两个数比较,绝对值大的可能大,原来的说法不正确.
故选:A.
7.解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是倒数等于它本身的数,
∴a=1,b=﹣1,c=0,d=±1,
∴原式=a﹣b+c2﹣|d|=1﹣(﹣1)+02﹣|±1|=2﹣1=1.
故选:D.
8.解:设2020在第n组,则1+3+5+7+(2n﹣1)=×2n×n=n2,
当n=44时,n2=1936;
当n=45时,n2=2025;
故2020在第45组,
∵2020﹣1936=84,
∴2020为第45组的第84个数.
故A2020=(45,84),
故选:D.
二.填空题(共8小题,满分32分)
9.解:的相反数是,
=,的倒数是2,
+(﹣5)=﹣5,﹣5的绝对值5.
故答案为:,2,5.
10.解:∵(±5)2=25,
∴平方等于25的数是±5,
故答案为:±5.
11.解:5 400 000=5.4×106万元.
故答案为5.4×106.
12.解:∵|a|=1,|b|=4,且a+b<0,
∴a=1,b=﹣4;a=﹣1,b=﹣4,
则a+b=﹣3或﹣5.
故答案为:﹣3或﹣5.
13.解:根据题意得:绝对值不大于3的所有整数有0,±1,±2,±3.
故答案为:0,±1,±2,±3.
14.解:由题意得:﹣1×3﹣(﹣1)=﹣3+1=﹣2,
﹣2×3﹣(﹣1)=﹣6+1=﹣5,
﹣5×3﹣(﹣1)=﹣15+1=﹣14<﹣5,
∴输出的结果是﹣14,
故答案为:﹣14.
15.解:根据题意得,x﹣2=0,y+3=0,
解得x=2,y=﹣3,
所以,yx=(﹣3)2=9.
故答案为:9.
16.解:设第n次跳到的点为an(n为自然数),
观察,发现规律:a0=1,a1=3,a2=5,a3=2,a4=1,a5=3,a6=5,a7=2,…,
∴a4n=1,a4n+1=3,a4+2=5,a4n+3=2.
∵2023=505×4+3,
∴经2023次跳后它停的点所对应的数为2.
故答案为:2.
三.解答题(共8小题,满分56分)
17.解:①﹣20+(﹣14)﹣(﹣18)﹣13
=﹣34+18﹣13
=﹣16﹣13
=﹣29
②(﹣56)×(﹣+)
=(﹣56)×﹣(﹣56)×+(﹣56)×
=﹣32+21﹣4
=﹣11﹣4
=﹣15
③2×(﹣3)2﹣5÷(﹣)×(﹣2)
=2×9+10×(﹣2)
=18﹣20
=﹣2
④﹣9×36
=(﹣9﹣)×36
=(﹣9)×36﹣×36
=﹣324﹣35
=﹣359
⑤﹣14﹣(1﹣0.5)××[2﹣(﹣3)2]
=﹣1﹣0.5××[﹣7]
=﹣1+
=
18.解:如图所示:
.
19.解:在数轴上把各数表示出来为:
用“<”连接各数为:﹣|﹣3.5|<﹣(+1)<0<1<﹣(﹣2)<4.
20.解:(1)200×3+(4﹣2﹣5)=597(辆),
故答案为:597;
((2)4﹣2﹣5+13﹣11+17﹣9=7(辆),
1400×60+7×(10+60)=84490(元).
答:该厂工人这一周的工资总额是84490元.
21.解:(1)若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是:(﹣7)×(﹣3)=21,
故答案为:21;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是:(﹣7)÷1=﹣7,
故答案为:﹣7;
(3)由题意可得,
如果抽取的数字是﹣7,﹣3,1,2,
则(﹣7)×(﹣3)+1+2=24,(﹣7+1﹣2)×(﹣3)=24;
如果抽取的数字是﹣3,1,2,5,
则(1﹣5)×(﹣3)×2=24,[5﹣(﹣3)]×(1+2)=24.
22.解:(1)由题意可得,
(2+3)t=8﹣(﹣12),
解得t=4,
点P表示的数为:﹣12+2×4=﹣12+8=﹣4,
故答案为:4,﹣4;
(2)相遇前,两只蚂蚁的距离为8.则(2+3)t=[8﹣(﹣12)]﹣8,得t=2.4;
相遇后,两只蚂蚁的距离为8.则(2+3)t=[8﹣(﹣12)]+8,得t=5.6;
故答案为:2.4或5.6.
23.解:(1)+++…+=1﹣.
2﹣22﹣23﹣24﹣25﹣26﹣…﹣22021+22022
=2﹣22022(1﹣)+22022
=2﹣22016+22+22016
=6;
(2)+++…+=1﹣×(1﹣)=1﹣.
(3)++++…+=1﹣.
故答案为:1﹣;1﹣;1﹣.
24.解:(1)|x﹣4|+|x+2|的最小值为4﹣(﹣2)=6,此时x的取值情况是﹣2≤x≤4;
(2)|x﹣3|+|x+2|+|x+6|的最小值为(﹣2+6)+0+(3+2)=9,此时x的取值情况是x=﹣2;
(3)∵|x﹣1|+|x+2|+|y﹣3|+|y+4|=10,
∴﹣2≤x≤1,﹣4≤y≤3,
∴2x+y的最大值为2×1+3=5,最小值为2×(﹣2)+(﹣4)=﹣8.
故2x+y的最大值为5,最小值为﹣8.
一.选择题(共8小题,满分32分)
1.如果收入200元记作+200元,那么支出150元记作( )
A.+150元 B.﹣150元 C.+50元 D.﹣50元
2.下列一组数:﹣8,2.7,,,0.66666…,0,2,0.080080008…,其中是无理数的有( )
A.0个 B.1个 C.2个 D.3个
3.在四包真空小包装火腿,每包以标准克数(450克)0为基数,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准的是( )
A.+2 B.﹣3 C.﹣1 D.+4
4.下列各组数中,互为相反数的是( )
A.2与 B.(﹣1)2与1 C.﹣1与(﹣1)3 D.﹣(﹣2)与﹣|﹣2|
5.下列运算正确的是( )
A. B.﹣7﹣2×5=﹣9×5=﹣45
C. D.﹣(﹣3)2=﹣9
6.下列说法正确的是( )
①有理数包括正有理数和负有理数 ②相反数大于本身的数是负数
③数轴上原点两侧的数互为相反数 ④两个数比较,绝对值大的反而小.
A.② B.①③ C.①② D.②③④
7.如果有理数a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是倒数等于它本身的数,那么式子a﹣b+c2﹣|d|的值是( )
A.﹣2 B.﹣1 C.0 D.1
8.把所有正整数从小到大排列,并按如下规律分组:(1),(2,3,4),(5,6,7,8,9),(10,11,12,13,14,15,16),…,现用等式AM=(i,j)表示正整数M是第i组第j个数(从左往右数),如A7=(3,3),则A2020=( )
A.(44,81) B.(44,82) C.(45,83) D.(45,84)
二.填空题(共8小题,满分32分)
9.的相反数是 ,的倒数是 ,+(﹣5)的绝对值为 .
10.平方等于25的数是 .
11.据测算,我国每年因沙漠造成的直接经济损失超过5 400 000万元,这个数用科学记数法表示为 万元.
12.若|a|=1,|b|=4,且a+b<0,则a+b= .
13.绝对值不大于3的所有整数有 .
14.如图所示是计算机某计算程序,若开始输入x=﹣1,则最后输出的结果是 .
15.若(x﹣2)2+|y+3|=0,则yx的值是 .
16.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2023次跳后它停的点所对应的数为 .
三.解答题(共8小题,满分56分)
17.计算
①﹣20+(﹣14)﹣(﹣18)﹣13
②(﹣56)×(﹣+)
③2×(﹣3)2﹣5÷(﹣)×(﹣2)
④﹣9×36(用简便方法)
⑤﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].
18.将有理数﹣12,0,20,﹣1.25,1,﹣|﹣12|,﹣(﹣5)分类.
19.在数轴上把下列各数表示出来,并用“<”连接各数.
﹣|﹣3.5|,1,0,﹣(﹣2),﹣(+1),4
20.某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负).
星期 一 二 三 四 五 六 日
增减 +4 ﹣2 ﹣5 +13 ﹣11 +17 ﹣9
(1)根据记录可知前三天共生产 辆;
(2)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖10元;少生产一辆扣10元,那么该厂工人这一周的工资总额是多少?
21.如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
(1)若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是 .
(2)若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是 .
(3)若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
22.如图,点A、B在数轴上表示的数分别为﹣12和8,两只蚂蚁M、N分别从A、B两点同时出发,相向而行.M的速度为2个单位长度/秒,N的速度为3个单位长度/秒.
(1)运动 秒钟时,两只蚂蚁相遇在点P;点P在数轴上表示的数是 ;
(2)若运动t秒钟时,两只蚂蚁的距离为8,则t的值是 .
23.利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合,请利用数形结合的思想解决下列问题.
(1)如图,一个边长为1的正方形,依次取正方形面积的、、、…、,根据图(1)我们可以知道:+++…+= .
利用上述公式计算:2﹣22﹣23﹣24﹣25﹣26﹣…﹣22021+22022.
(2)如图(2),一个边长为1的正方形,依次取剩余部分的,根据图示计算:+++…+= .
(3)如图(3)是一个边长为1的正方形,根据图示计算:++++…+= .
24.我们知道,|x|表示x在数轴上对应的点到原点的距离我们可以把|x|看作|x﹣0|,所以,|x﹣3|就表示x在数轴上对应的点到3的距离,|x+1|=|x﹣(﹣1)|就表示x在数轴上对应的点到﹣1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求|x﹣4|+|x+2|的最小值,并写出此时x的取值情况;
(2)求|x﹣3|+|x+2|+|x+6|的最小值,并写出此时x的取值情况;
(3)已知|x﹣1|+|x+2|+|y﹣3|+|y+4|=10,求2x+y的最大值和最小值.
参考答案
一.选择题(共8小题,满分32分)
1.解:因为正”和“负”相对,所以,如果收入200元记作+200元,那么支出150元记作﹣150元.
故选:B.
2.解:,0.080080008…是无理数,
故选:C.
3.解:A、+2的绝对值是2;
B、﹣3的绝对值是3;
C、﹣1的绝对值是1;
D、+4的绝对值是4.
C选项的绝对值最小.
故选:C.
4.解:A、2与不是互为相反数,故本选项错误;
B、(﹣1)2与1相等,不是互为相反数,故本选项错误;
C、﹣1与(﹣1)3相等,不是互为相反数,故本选项错误;
D、﹣(﹣2)=2,﹣|﹣2|=﹣2,是互为相反数,故本选项正确.
故选:D.
5.解:A、,故选项错误;
B、﹣7﹣2×5=﹣7﹣10=﹣17,故选项错误;
C、,故选项错误;
D、﹣(﹣3)2=﹣9,故选项正确.
故选:D.
6.解:①有理数包括正有理数,负有理数和0,原来的说法不正确.
②说法正确.
③数轴上原点两侧的数不一定互为相反数,原来的说法不正确.
④两个数比较,绝对值大的可能大,原来的说法不正确.
故选:A.
7.解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,d是倒数等于它本身的数,
∴a=1,b=﹣1,c=0,d=±1,
∴原式=a﹣b+c2﹣|d|=1﹣(﹣1)+02﹣|±1|=2﹣1=1.
故选:D.
8.解:设2020在第n组,则1+3+5+7+(2n﹣1)=×2n×n=n2,
当n=44时,n2=1936;
当n=45时,n2=2025;
故2020在第45组,
∵2020﹣1936=84,
∴2020为第45组的第84个数.
故A2020=(45,84),
故选:D.
二.填空题(共8小题,满分32分)
9.解:的相反数是,
=,的倒数是2,
+(﹣5)=﹣5,﹣5的绝对值5.
故答案为:,2,5.
10.解:∵(±5)2=25,
∴平方等于25的数是±5,
故答案为:±5.
11.解:5 400 000=5.4×106万元.
故答案为5.4×106.
12.解:∵|a|=1,|b|=4,且a+b<0,
∴a=1,b=﹣4;a=﹣1,b=﹣4,
则a+b=﹣3或﹣5.
故答案为:﹣3或﹣5.
13.解:根据题意得:绝对值不大于3的所有整数有0,±1,±2,±3.
故答案为:0,±1,±2,±3.
14.解:由题意得:﹣1×3﹣(﹣1)=﹣3+1=﹣2,
﹣2×3﹣(﹣1)=﹣6+1=﹣5,
﹣5×3﹣(﹣1)=﹣15+1=﹣14<﹣5,
∴输出的结果是﹣14,
故答案为:﹣14.
15.解:根据题意得,x﹣2=0,y+3=0,
解得x=2,y=﹣3,
所以,yx=(﹣3)2=9.
故答案为:9.
16.解:设第n次跳到的点为an(n为自然数),
观察,发现规律:a0=1,a1=3,a2=5,a3=2,a4=1,a5=3,a6=5,a7=2,…,
∴a4n=1,a4n+1=3,a4+2=5,a4n+3=2.
∵2023=505×4+3,
∴经2023次跳后它停的点所对应的数为2.
故答案为:2.
三.解答题(共8小题,满分56分)
17.解:①﹣20+(﹣14)﹣(﹣18)﹣13
=﹣34+18﹣13
=﹣16﹣13
=﹣29
②(﹣56)×(﹣+)
=(﹣56)×﹣(﹣56)×+(﹣56)×
=﹣32+21﹣4
=﹣11﹣4
=﹣15
③2×(﹣3)2﹣5÷(﹣)×(﹣2)
=2×9+10×(﹣2)
=18﹣20
=﹣2
④﹣9×36
=(﹣9﹣)×36
=(﹣9)×36﹣×36
=﹣324﹣35
=﹣359
⑤﹣14﹣(1﹣0.5)××[2﹣(﹣3)2]
=﹣1﹣0.5××[﹣7]
=﹣1+
=
18.解:如图所示:
.
19.解:在数轴上把各数表示出来为:
用“<”连接各数为:﹣|﹣3.5|<﹣(+1)<0<1<﹣(﹣2)<4.
20.解:(1)200×3+(4﹣2﹣5)=597(辆),
故答案为:597;
((2)4﹣2﹣5+13﹣11+17﹣9=7(辆),
1400×60+7×(10+60)=84490(元).
答:该厂工人这一周的工资总额是84490元.
21.解:(1)若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是:(﹣7)×(﹣3)=21,
故答案为:21;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是:(﹣7)÷1=﹣7,
故答案为:﹣7;
(3)由题意可得,
如果抽取的数字是﹣7,﹣3,1,2,
则(﹣7)×(﹣3)+1+2=24,(﹣7+1﹣2)×(﹣3)=24;
如果抽取的数字是﹣3,1,2,5,
则(1﹣5)×(﹣3)×2=24,[5﹣(﹣3)]×(1+2)=24.
22.解:(1)由题意可得,
(2+3)t=8﹣(﹣12),
解得t=4,
点P表示的数为:﹣12+2×4=﹣12+8=﹣4,
故答案为:4,﹣4;
(2)相遇前,两只蚂蚁的距离为8.则(2+3)t=[8﹣(﹣12)]﹣8,得t=2.4;
相遇后,两只蚂蚁的距离为8.则(2+3)t=[8﹣(﹣12)]+8,得t=5.6;
故答案为:2.4或5.6.
23.解:(1)+++…+=1﹣.
2﹣22﹣23﹣24﹣25﹣26﹣…﹣22021+22022
=2﹣22022(1﹣)+22022
=2﹣22016+22+22016
=6;
(2)+++…+=1﹣×(1﹣)=1﹣.
(3)++++…+=1﹣.
故答案为:1﹣;1﹣;1﹣.
24.解:(1)|x﹣4|+|x+2|的最小值为4﹣(﹣2)=6,此时x的取值情况是﹣2≤x≤4;
(2)|x﹣3|+|x+2|+|x+6|的最小值为(﹣2+6)+0+(3+2)=9,此时x的取值情况是x=﹣2;
(3)∵|x﹣1|+|x+2|+|y﹣3|+|y+4|=10,
∴﹣2≤x≤1,﹣4≤y≤3,
∴2x+y的最大值为2×1+3=5,最小值为2×(﹣2)+(﹣4)=﹣8.
故2x+y的最大值为5,最小值为﹣8.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
