苏科版九年级数学上册 第2章对称图形——圆 单元达标测试题(含答案解析)
文档属性
| 名称 | 苏科版九年级数学上册 第2章对称图形——圆 单元达标测试题(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 340.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 16:22:13 | ||
图片预览

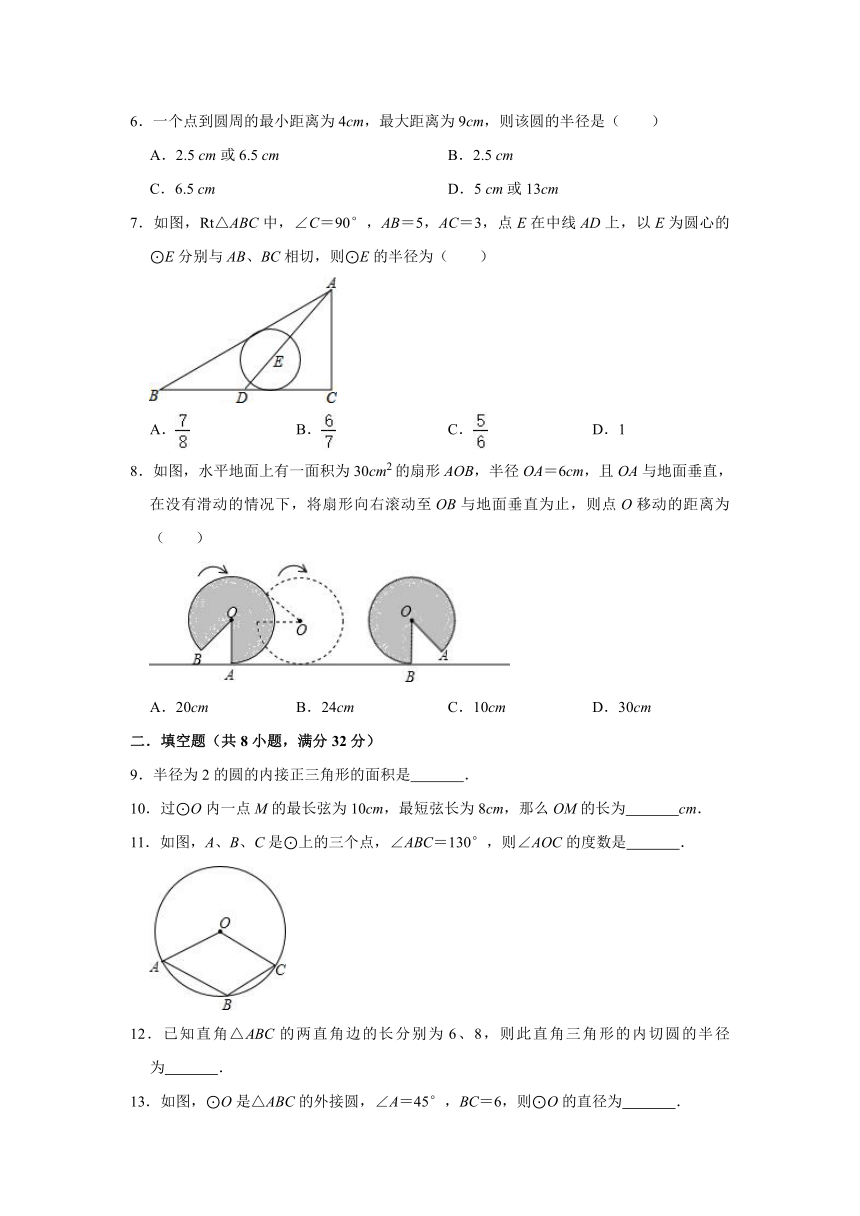
文档简介
2022-2023学年苏科版九年级数学上册《第2章对称图形——圆》单元达标测试题(附答案)
一.选择题(共8小题,满分32分)
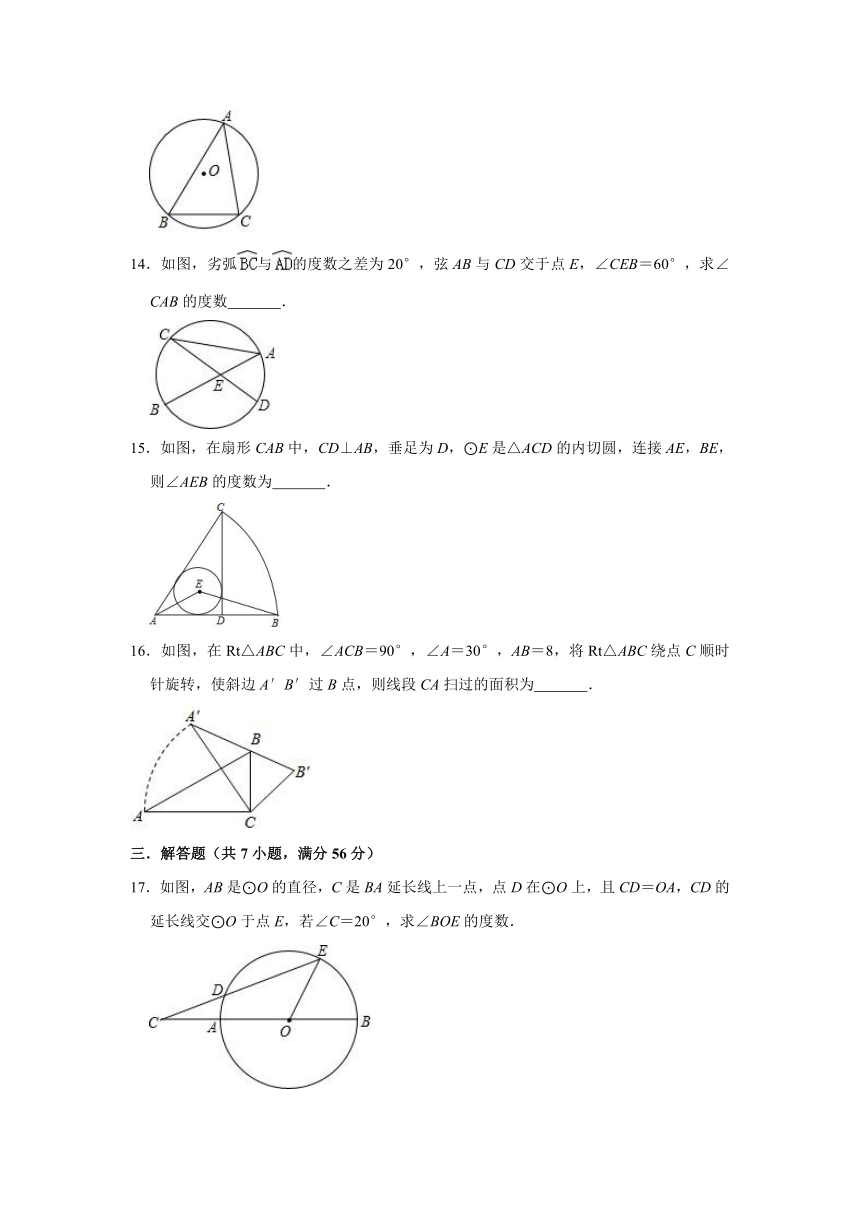
1.下列命题中,正确的是( )
A.平面上三个点确定一个圆 B.等弧所对的圆周角相等
C.平分弦的直径垂直于这条弦 D.与某圆一条半径垂直的直线是该圆的切线
2.如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
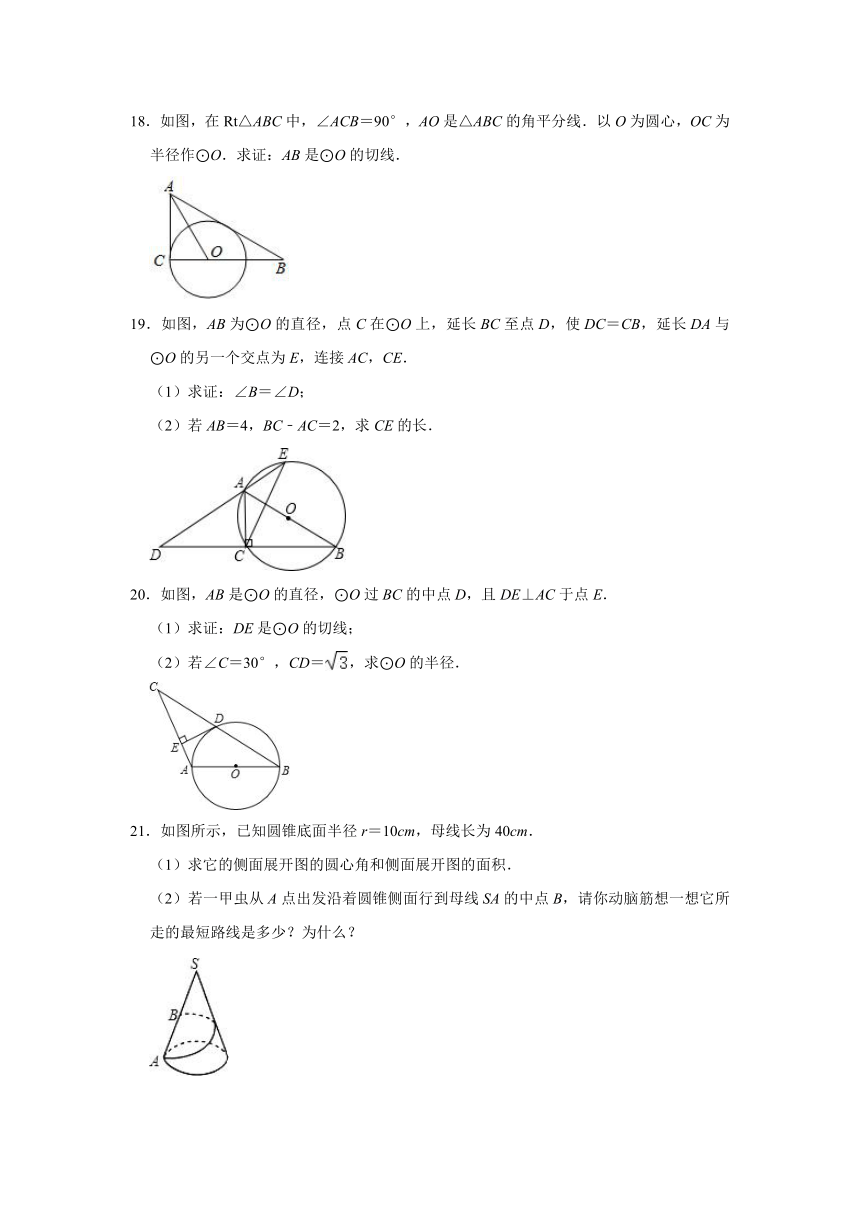
A.55° B.60° C.65° D.70°
3.已知矩形ABCD的边AB=5,BC=12,以点A为圆心作圆A,使B、C、D三点至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是( )
A.5≤r≤13 B.5≤r≤12 C.5<r<12 D.5<r<13
4.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
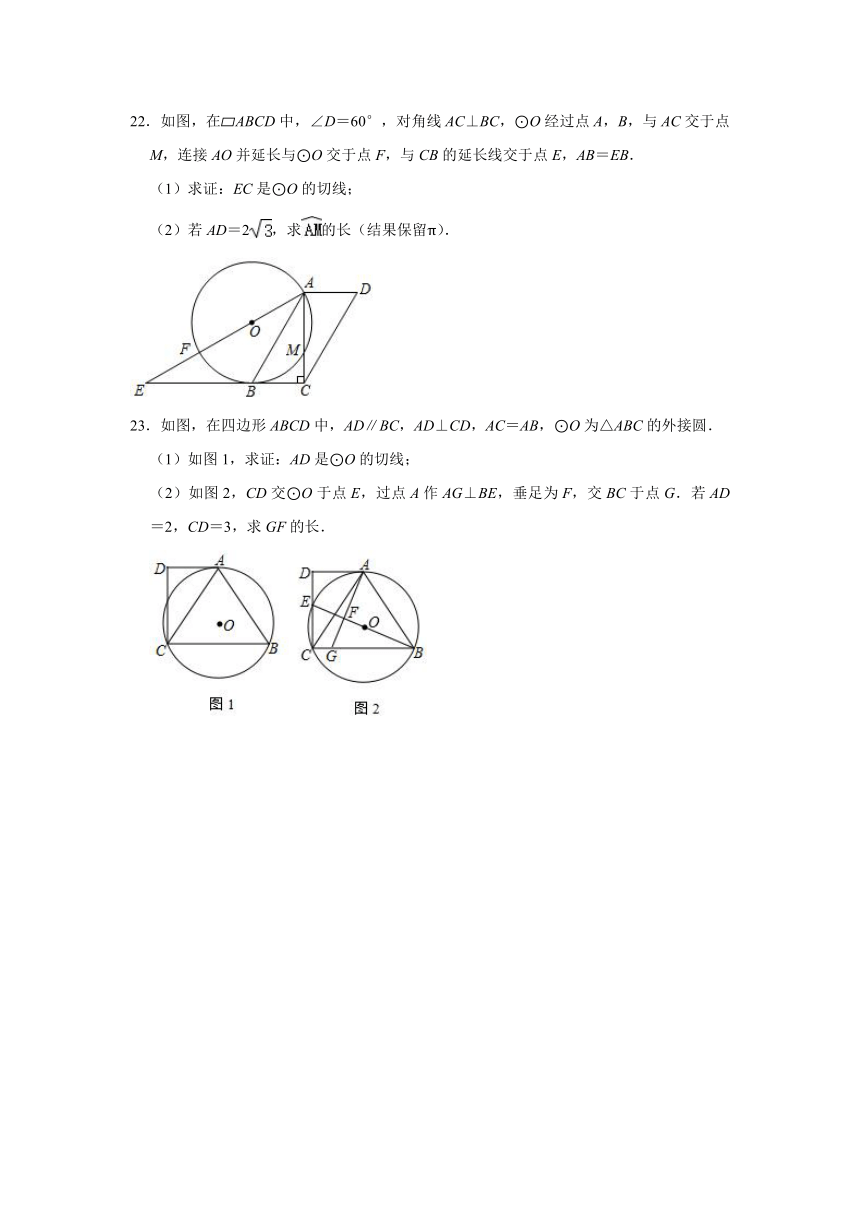
5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
A.15° B.28° C.29° D.34°
6.一个点到圆周的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5 cm或6.5 cm B.2.5 cm
C.6.5 cm D.5 cm或13cm
7.如图,Rt△ABC中,∠C=90°,AB=5,AC=3,点E在中线AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径为( )
A. B. C. D.1
8.如图,水平地面上有一面积为30cm2的扇形AOB,半径OA=6cm,且OA与地面垂直,在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动的距离为( )
A.20cm B.24cm C.10cm D.30cm
二.填空题(共8小题,满分32分)
9.半径为2的圆的内接正三角形的面积是 .
10.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,那么OM的长为 cm.
11.如图,A、B、C是⊙上的三个点,∠ABC=130°,则∠AOC的度数是 .
12.已知直角△ABC的两直角边的长分别为6、8,则此直角三角形的内切圆的半径为 .
13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=6,则⊙O的直径为 .
14.如图,劣弧与的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,求∠CAB的度数 .
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .
16.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为 .
三.解答题(共7小题,满分56分)
17.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=20°,求∠BOE的度数.
18.如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.求证:AB是⊙O的切线.
19.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
20.如图,AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=,求⊙O的半径.
21.如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角和侧面展开图的面积.
(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
22.如图,在 ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E,AB=EB.
(1)求证:EC是⊙O的切线;
(2)若AD=2,求的长(结果保留π).
23.如图,在四边形ABCD中,AD∥BC,AD⊥CD,AC=AB,⊙O为△ABC的外接圆.
(1)如图1,求证:AD是⊙O的切线;
(2)如图2,CD交⊙O于点E,过点A作AG⊥BE,垂足为F,交BC于点G.若AD=2,CD=3,求GF的长.
参考答案
一.选择题(共8小题,满分32分)
1.解:A.三个点不共线的点确定一个平面,故A不正确;
B.由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角 相等,故选项B正确;
C.平分弦的直径垂直于弦,被平分的弦不能是直径,故此选项错误;
D.与某圆一条半径垂直的直线是该圆的切线,错误,正确的应该是:一条直线垂直于圆的半径的外端,这条直线一定就是圆的切线.故此选项错误;
故选:B.
2.解:连接OD,OC,
∵∠ABC=50°,
∴∠AOC=2∠ABC=100°,
∴AC弧=100°,
∵D是弧AC的中点,
∴AD弧=50°,
∴BD弧=130°,
∴∠DOB=130°,
∴∠DAB=∠DOB=65°
故选:C.
3.解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=12,
在Rt△ABC中,AC==13,
∵以点A为圆心作圆A,使B、C、D三点至少有一点在圆内,且至少有一点在圆外,
即点B在圆内,点C在圆外,
∴5<r<13.
故选:D.
4.解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CDB都对,
∴∠BOC=2∠CDB,又∠CDB=20°,
∴∠BOC=40°,
又∵CE为圆O的切线,
∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.
故选:B.
5.解:根据圆周角定理可知:圆周角的度数等于它所对的弧的度数的一半,
根据量角器的读数方法可得:(86°﹣30°)÷2=28°.
故选:B.
6.解:当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是13cm,因而半径是6.5cm;
当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是5cm,因而半径是2.5cm.
故选:A.
7.解:作EH⊥AC于H,EF⊥BC于F,EG⊥AB于G,连接EB,EC,设⊙E的半径为R,如图,
∵∠C=90°,AB=5,AC=3,
∴BC==4,
而AD为中线,
∴DC=2,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EG=EF=R,
∴HC=R,AH=3﹣R,
∵EH∥BC,
∴△AEH∽△ADC,
∴EH:CD=AH:AC,即EH=,
∵S△ABE+S△BCE+S△ACE=S△ABC,
∴×5×R+×4×R+×3×(3﹣R)=×3×4,
∴R=.
故选:B.
8.解:由题意可得出:点O移动的距离为扇形的弧长,
∵面积为30cm2的扇形AOB,半径OA=6cm,
∴30=×l×6,
∴扇形弧长为:l=10(cm).
故选:C.
二.填空题(共8小题,满分32分)
9.解:如图所示,连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,BD=CD,
∠BOC==120°,
则∠OBC=30°,
∴OD=OB=1,
由勾股定理得,BD==,
∴BC=2BD=2,
∴△ABC的面积=3S△OBC=3××2×1=3,
故答案为:3.
10.解:由已知可知,最长的弦是过M的直径AB最短的是垂直于直径的弦CD,
最短的是垂直平分直径的弦CD,
已知AB=10cm,CD=8cm,
则OD=5cm,MD=4cm,
由勾股定理得OM=3cm.
11.解:如图,在优弧AC上取点D,连接AD,CD,
∵∠ABC=130°,
∴∠ADC=180°﹣∠ABC=50°,
∴∠AOC=2∠ADC=100°.
故答案为:100°.
12.解:∵直角三角形的两直角边分别为6,8,
∴直角三角形的斜边是:=10,
∴内切圆的半径为:(6+8﹣10)÷2=2.
故答案为:2.
13.解:连接OB、OC,如图,
∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=BC=3,
∴⊙O的直径为6.
故答案为:6.
14.解:由题意,弧BC与弧AD的度数之差为20°,
∴两弧所对圆心角相差20°,
∴2∠A﹣2∠C=20°,
∴∠A﹣∠C=10°…①;
∵∠CEB是△AEC的外角,
∴∠A+∠C=∠CEB=60°…②;
①+②,得:2∠A=70°,即∠A=35°.
故答案为:35°.
15.解:如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180°﹣(∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
16.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=4,∠ABC=90°﹣∠A=60°,
∴AC===4,
∵将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,
∴CB′=CB,∠B′=∠ABC=60°,∠A′CB′=∠ACB=90°,
∴△BCB′是等边三角形,
∴∠BCB′=60°,
∴∠A′CB=90°﹣60°=30°,
∴∠ACA′=∠ACB﹣∠A′CB=90°﹣30°=60°,
∴线段CA扫过的面积为=8π,
故答案为:8π.
三.解答题(共7小题,满分56分)
17.解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°.
18.证明:如图,过点O作OF⊥AB于点F,
∵AO平分∠CAB,OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线.
19.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
20.(1)证明:连接OD.
因为D是BC的中点,O是AB的中点,
∴OD∥AC,
∴∠CED=∠ODE.
∵DE⊥AC,
∴∠CED=∠ODE=90°.
∴OD⊥DE,OD是圆的半径,
∴DE是⊙O的切线.
(2)连接AD,
∵OD∥AC,
∴∠C=∠ODB=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=90°,
∵CD=,
∴∠ADO=60°,AD=1,
∴AD=OD=OA=1.
21.解:(1)=2π×10,
解得n=90.
圆锥侧面展开图的面积=π×10×40=400πcm2.
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
在Rt△ASB中,SA=40,SB=20,
∴AB=20(cm).
∴甲虫走的最短路线的长度是20cm.
22.(1)证明:连接OB,连接OM,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D=60°,
∵AC⊥BC,
∴∠ACB=90°,
∴∠BAC=30°,
∵BE=AB,
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE=60°,
∴∠E=∠BAE=30°,
∵OA=OB,
∴∠ABO=∠OAB=30°,
∴∠OBC=30°+60°=90°,
∴OB⊥CE,
∴EC是⊙O的切线;
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=2,
过O作OH⊥AM于H,
则四边形OBCH是矩形,
∴OH=BC=2,
∴OA=4,∠AOM=2∠AOH=60°,
∴的长度==.
23.(1)证明:如图1,连接OA,OB,OC.
在△OAC和△OAB中,
,
∴△OAC≌△OAB(SSS),
∴∠OAC=∠OAB,
∴AO平分∠BAC,
∴AO⊥BC.
又∵AD∥BC,
∴AD⊥AO,
∴AD是⊙O的切线.
(2)如图2,连接AE.
∵∠BCE=90°,
∴∠BAE=90°.
又∵AF⊥BE,
∴∠AFB=90°.
∵∠BAG+∠EAF=∠AEB+∠EAF=90°,
∴∠BAG=∠AEB.
∵∠ABC=∠ACB=∠AEB,
∴∠BAG=∠ABC,
∴AG=BG.
在△ADC和△AFB中,
,
∴△ADC≌△AFB(AAS),
∴AF=AD=2,BF=CD=3.
设FG=x,在Rt△BFG中,FG=x,BF=3,BG=AG=x+2,
∴FG2+BF2=BG2,即x2+32=(x+2)2,
∴x=,
∴FG=.
一.选择题(共8小题,满分32分)
1.下列命题中,正确的是( )
A.平面上三个点确定一个圆 B.等弧所对的圆周角相等
C.平分弦的直径垂直于这条弦 D.与某圆一条半径垂直的直线是该圆的切线
2.如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
A.55° B.60° C.65° D.70°
3.已知矩形ABCD的边AB=5,BC=12,以点A为圆心作圆A,使B、C、D三点至少有一点在圆内,且至少有一点在圆外,则⊙A的半径r的取值范围是( )
A.5≤r≤13 B.5≤r≤12 C.5<r<12 D.5<r<13
4.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
A.15° B.28° C.29° D.34°
6.一个点到圆周的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5 cm或6.5 cm B.2.5 cm
C.6.5 cm D.5 cm或13cm
7.如图,Rt△ABC中,∠C=90°,AB=5,AC=3,点E在中线AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径为( )
A. B. C. D.1
8.如图,水平地面上有一面积为30cm2的扇形AOB,半径OA=6cm,且OA与地面垂直,在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动的距离为( )
A.20cm B.24cm C.10cm D.30cm
二.填空题(共8小题,满分32分)
9.半径为2的圆的内接正三角形的面积是 .
10.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,那么OM的长为 cm.
11.如图,A、B、C是⊙上的三个点,∠ABC=130°,则∠AOC的度数是 .
12.已知直角△ABC的两直角边的长分别为6、8,则此直角三角形的内切圆的半径为 .
13.如图,⊙O是△ABC的外接圆,∠A=45°,BC=6,则⊙O的直径为 .
14.如图,劣弧与的度数之差为20°,弦AB与CD交于点E,∠CEB=60°,求∠CAB的度数 .
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为 .
16.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=8,将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,则线段CA扫过的面积为 .
三.解答题(共7小题,满分56分)
17.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=20°,求∠BOE的度数.
18.如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.求证:AB是⊙O的切线.
19.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
20.如图,AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠C=30°,CD=,求⊙O的半径.
21.如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角和侧面展开图的面积.
(2)若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
22.如图,在 ABCD中,∠D=60°,对角线AC⊥BC,⊙O经过点A,B,与AC交于点M,连接AO并延长与⊙O交于点F,与CB的延长线交于点E,AB=EB.
(1)求证:EC是⊙O的切线;
(2)若AD=2,求的长(结果保留π).
23.如图,在四边形ABCD中,AD∥BC,AD⊥CD,AC=AB,⊙O为△ABC的外接圆.
(1)如图1,求证:AD是⊙O的切线;
(2)如图2,CD交⊙O于点E,过点A作AG⊥BE,垂足为F,交BC于点G.若AD=2,CD=3,求GF的长.
参考答案
一.选择题(共8小题,满分32分)
1.解:A.三个点不共线的点确定一个平面,故A不正确;
B.由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角 相等,故选项B正确;
C.平分弦的直径垂直于弦,被平分的弦不能是直径,故此选项错误;
D.与某圆一条半径垂直的直线是该圆的切线,错误,正确的应该是:一条直线垂直于圆的半径的外端,这条直线一定就是圆的切线.故此选项错误;
故选:B.
2.解:连接OD,OC,
∵∠ABC=50°,
∴∠AOC=2∠ABC=100°,
∴AC弧=100°,
∵D是弧AC的中点,
∴AD弧=50°,
∴BD弧=130°,
∴∠DOB=130°,
∴∠DAB=∠DOB=65°
故选:C.
3.解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=12,
在Rt△ABC中,AC==13,
∵以点A为圆心作圆A,使B、C、D三点至少有一点在圆内,且至少有一点在圆外,
即点B在圆内,点C在圆外,
∴5<r<13.
故选:D.
4.解:连接OC,如图所示:
∵圆心角∠BOC与圆周角∠CDB都对,
∴∠BOC=2∠CDB,又∠CDB=20°,
∴∠BOC=40°,
又∵CE为圆O的切线,
∴OC⊥CE,即∠OCE=90°,
则∠E=90°﹣40°=50°.
故选:B.
5.解:根据圆周角定理可知:圆周角的度数等于它所对的弧的度数的一半,
根据量角器的读数方法可得:(86°﹣30°)÷2=28°.
故选:B.
6.解:当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是13cm,因而半径是6.5cm;
当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是5cm,因而半径是2.5cm.
故选:A.
7.解:作EH⊥AC于H,EF⊥BC于F,EG⊥AB于G,连接EB,EC,设⊙E的半径为R,如图,
∵∠C=90°,AB=5,AC=3,
∴BC==4,
而AD为中线,
∴DC=2,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EG=EF=R,
∴HC=R,AH=3﹣R,
∵EH∥BC,
∴△AEH∽△ADC,
∴EH:CD=AH:AC,即EH=,
∵S△ABE+S△BCE+S△ACE=S△ABC,
∴×5×R+×4×R+×3×(3﹣R)=×3×4,
∴R=.
故选:B.
8.解:由题意可得出:点O移动的距离为扇形的弧长,
∵面积为30cm2的扇形AOB,半径OA=6cm,
∴30=×l×6,
∴扇形弧长为:l=10(cm).
故选:C.
二.填空题(共8小题,满分32分)
9.解:如图所示,连接OB、OC,作OD⊥BC于D,
则∠ODB=90°,BD=CD,
∠BOC==120°,
则∠OBC=30°,
∴OD=OB=1,
由勾股定理得,BD==,
∴BC=2BD=2,
∴△ABC的面积=3S△OBC=3××2×1=3,
故答案为:3.
10.解:由已知可知,最长的弦是过M的直径AB最短的是垂直于直径的弦CD,
最短的是垂直平分直径的弦CD,
已知AB=10cm,CD=8cm,
则OD=5cm,MD=4cm,
由勾股定理得OM=3cm.
11.解:如图,在优弧AC上取点D,连接AD,CD,
∵∠ABC=130°,
∴∠ADC=180°﹣∠ABC=50°,
∴∠AOC=2∠ADC=100°.
故答案为:100°.
12.解:∵直角三角形的两直角边分别为6,8,
∴直角三角形的斜边是:=10,
∴内切圆的半径为:(6+8﹣10)÷2=2.
故答案为:2.
13.解:连接OB、OC,如图,
∵∠BOC=2∠A=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=BC=3,
∴⊙O的直径为6.
故答案为:6.
14.解:由题意,弧BC与弧AD的度数之差为20°,
∴两弧所对圆心角相差20°,
∴2∠A﹣2∠C=20°,
∴∠A﹣∠C=10°…①;
∵∠CEB是△AEC的外角,
∴∠A+∠C=∠CEB=60°…②;
①+②,得:2∠A=70°,即∠A=35°.
故答案为:35°.
15.解:如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180°﹣(∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
16.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=4,∠ABC=90°﹣∠A=60°,
∴AC===4,
∵将Rt△ABC绕点C顺时针旋转,使斜边A′B′过B点,
∴CB′=CB,∠B′=∠ABC=60°,∠A′CB′=∠ACB=90°,
∴△BCB′是等边三角形,
∴∠BCB′=60°,
∴∠A′CB=90°﹣60°=30°,
∴∠ACA′=∠ACB﹣∠A′CB=90°﹣30°=60°,
∴线段CA扫过的面积为=8π,
故答案为:8π.
三.解答题(共7小题,满分56分)
17.解:连接OD,
∵CD=OA=OD,∠C=20°,
∴∠ODE=2∠C=40°,
∵OD=OE,
∴∠E=∠EDO=40°,
∴∠EOB=∠C+∠E=40°+20°=60°.
18.证明:如图,过点O作OF⊥AB于点F,
∵AO平分∠CAB,OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线.
19.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
20.(1)证明:连接OD.
因为D是BC的中点,O是AB的中点,
∴OD∥AC,
∴∠CED=∠ODE.
∵DE⊥AC,
∴∠CED=∠ODE=90°.
∴OD⊥DE,OD是圆的半径,
∴DE是⊙O的切线.
(2)连接AD,
∵OD∥AC,
∴∠C=∠ODB=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=90°,
∵CD=,
∴∠ADO=60°,AD=1,
∴AD=OD=OA=1.
21.解:(1)=2π×10,
解得n=90.
圆锥侧面展开图的面积=π×10×40=400πcm2.
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
在Rt△ASB中,SA=40,SB=20,
∴AB=20(cm).
∴甲虫走的最短路线的长度是20cm.
22.(1)证明:连接OB,连接OM,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D=60°,
∵AC⊥BC,
∴∠ACB=90°,
∴∠BAC=30°,
∵BE=AB,
∴∠E=∠BAE,
∵∠ABC=∠E+∠BAE=60°,
∴∠E=∠BAE=30°,
∵OA=OB,
∴∠ABO=∠OAB=30°,
∴∠OBC=30°+60°=90°,
∴OB⊥CE,
∴EC是⊙O的切线;
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=2,
过O作OH⊥AM于H,
则四边形OBCH是矩形,
∴OH=BC=2,
∴OA=4,∠AOM=2∠AOH=60°,
∴的长度==.
23.(1)证明:如图1,连接OA,OB,OC.
在△OAC和△OAB中,
,
∴△OAC≌△OAB(SSS),
∴∠OAC=∠OAB,
∴AO平分∠BAC,
∴AO⊥BC.
又∵AD∥BC,
∴AD⊥AO,
∴AD是⊙O的切线.
(2)如图2,连接AE.
∵∠BCE=90°,
∴∠BAE=90°.
又∵AF⊥BE,
∴∠AFB=90°.
∵∠BAG+∠EAF=∠AEB+∠EAF=90°,
∴∠BAG=∠AEB.
∵∠ABC=∠ACB=∠AEB,
∴∠BAG=∠ABC,
∴AG=BG.
在△ADC和△AFB中,
,
∴△ADC≌△AFB(AAS),
∴AF=AD=2,BF=CD=3.
设FG=x,在Rt△BFG中,FG=x,BF=3,BG=AG=x+2,
∴FG2+BF2=BG2,即x2+32=(x+2)2,
∴x=,
∴FG=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
