华师大版数学九年级下册 第27章综合素质评(含答案)
文档属性
| 名称 | 华师大版数学九年级下册 第27章综合素质评(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 17:25:43 | ||
图片预览




文档简介
第27章综合素质评价
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内 C.点P在⊙O上 D.无法确定
2.【教材P40练习T2变式】如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.给出下列四个结论,其中正确的结论为( )
A.三点确定一个圆 B.直径是最长的弦
C.圆周角是圆心角的一半 D.长度相等的弧是等弧
4.【2022·兰州】如图,△ABC内接于⊙O,CD是⊙O的直径,∠ACD=40°,则
∠B=( )
A.70° B.60° C.50° D.40°
5.【2022·自贡】P为⊙O外一点,PT与⊙O相切于点T,OP=10,∠OPT=30°,则PT长为( )
A.5 B.5 C.8 D.9
6.【2022·青岛一模】如图,在Rt△ABC中,∠C=90°,sin B=,AC=5 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
7.【2022·清苑区一模】已知△ABC和△ABD有相同的外心,∠D=70°,则∠C的度数是( )
A.70° B.110° C.70°或110° D.不能确定
8.【教材P55习题T4改编】【2022·娄底】如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与三角形ABC的面积之比是( )
A. B. C. D.
9.已知一弧长为l的弧所对的圆心角为120°,那么它所对的弦长为( )
A.l B.l C.l D.l
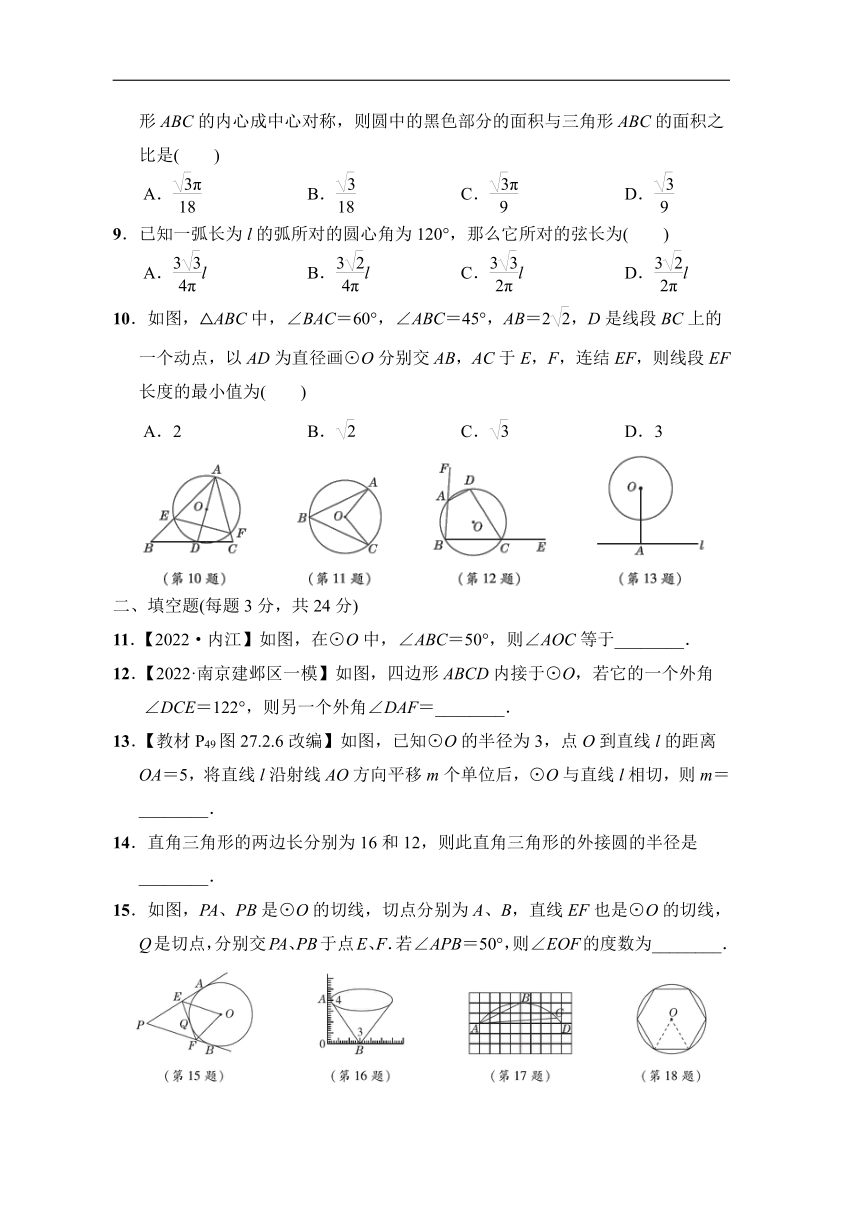
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF,则线段EF长度的最小值为( )
A.2 B. C. D.3
二、填空题(每题3分,共24分)
11.【2022·内江】如图,在⊙O中,∠ABC=50°,则∠AOC等于________.
12.【2022·南京建邺区一模】如图,四边形ABCD内接于⊙O,若它的一个外角
∠DCE=122°,则另一个外角∠DAF=________.
13.【教材P49图27.2.6改编】如图,已知⊙O的半径为3,点O到直线l的距离OA=5,将直线l沿射线AO方向平移m个单位后,⊙O与直线l相切,则m=________.
14.直角三角形的两边长分别为16和12,则此直角三角形的外接圆的半径是________.
15.如图,PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,分别交PA、PB于点E、F.若∠APB=50°,则∠EOF的度数为________.
16.一个圆锥形漏斗,某同学测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
17.如图所示的网格中,每个小正方形的边长均为1,点A、B、D均在小正方形的顶点上,且点B、C在上, ∠BAC=22.5°,则的长为________cm.
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,由此求得圆周率π的近似值.如图,设半径为r的圆内接正n边形的周长为C,圆的直径为d,当n=6时,π≈==3,则当n=12时,π≈≈________.(结果精确到0.01,参考数据:sin 15°=cos 75°≈0.259,sin 75°=cos 15°≈0.966)
三、解答题(19、20题每题10分,21、22题每题11分,23、24题每题12分,共66分)
19.【2022·怀化】如图,点A,B,C,D在⊙O上,=.求证:
(1)AC=BD;
(2)△ABE∽△DCE.
20.【教材P52练习T2变式】如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
21.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC、PD,切点分别为C、D,连结OP、CD.
(1)求证:OP⊥CD;
(2)连结AD、BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
22.如图,是一座拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱所在圆的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要通过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
23.【2022·滨州】如图,已知AC为⊙O的直径,直线PA与⊙O相切于点A,直线PD经过⊙O上的点B且∠CBD=∠CAB,连结OP交AB于点M.求证:
(1)PD是⊙O的切线;
(2)AM2=OM·PM.
24.如图①,已知抛物线y=ax2-x-4(a≠0)与y轴交于点A,与x轴交于点B、C,点C的坐标为(-2,0).
(1)求a的值和直线AB的函数表达式;
(2)如图②,连结AC,P是抛物线上一动点,且在直线AB的下方,过点P作y轴的平行线,交线段AB于点F,以PF为直径的⊙M与AB的另一个交点为E,连结PE.求劣弧EF长的最大值.
答案
一、1.A 2.D 3.B 4.C 5.A 6.A 7.C 8.A
9.C 点拨:设该弧所在⊙O的半径为r,所对的弦为AB.如图,过点O作OC⊥AB于点C.∵∠AOB=120°,∴的长为=l,则r=l.
∵∠AOB=120°,∴∠OBC=30°,∴OC=OB,
∴BC==l,∴AB=2BC=l.
10.C 点拨:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径
AD最短,连结OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=2,
∴AD=BD=2,即此时圆的直径为2,
由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OE·sin∠EOH=1×=,
∴EF=2EH=.
故选C.
二、11.100° 12.58° 13.2或8
14.8或10 15.65°
16.15π 17.
18.3.11 点拨:圆的内接正十二边形被半径分成12个如图所示的等腰三角形,
其顶角为30°.作OH⊥AB于点H,则∠AOH=15°.∵AO=BO=r,
∴在Rt△AOH中,sin∠AOH=,即sin 15°=,∴AH=r×sin 15°,
∴AB=2AH=2r×sin 15°,∴C=12×2r×sin 15°=24r×sin 15°.
又∵d=2r,∴π≈=≈3.11.
三、19.证明:(1)∵=,
∴=,
∴AC=BD.
(2)∵∠A=∠D,∠B=∠C,
∴△ABE∽△DCE.
20.解:(1)∵AB是⊙O的直径,AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
21.(1)证明:连结OD、OC,∵PD、PC是⊙O的切线,
∴PD=PC.
∵OD=OC,∴P、O在CD的中垂线上,
∴OP⊥CD.
(2)解:∵OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,
∴△COD是等边三角形.
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP==.
22.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设桥拱所在圆的半径为r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱所在圆的半径为50米.
(2)这艘轮船能顺利通过.理由如下:
如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM.
易知DE⊥MN,
∴MD=30米,
∴DE==40米.
∵EF=EC-CF=30米,
∴DF=DE-EF=10米.
∵10米>9米,
∴这艘轮船能顺利通过.
23.证明:(1)连结OB,如图所示.
∵OB=OC,
∴∠OCB=∠OBC.
∵AC是⊙O的直径,
∴∠CBA=90°.
∴∠CAB+∠OCB=90°.
∵∠CBD=∠CAB,
∴∠CBD+∠OBC=90°.
∴∠OBD=90°.
又∵OB是⊙O的半径,
∴PD是⊙O的切线.
(2)由PD是⊙O的切线,直线PA与⊙O相切,易得PO垂直平分AB.
∴∠AMP=∠AMO=90°.
∴∠APM+∠PAM=90°.
∵∠OAP=90°,
∴∠PAM+∠OAM=90°.
∴∠APM=∠OAM.
∴△OAM∽△APM.
∴=.
∴AM2=OM·PM.
24.解:(1)把C(-2,0)的坐标代入抛物线y=ax2-x-4(a≠0),
即0=a×(-2)2-(-2)-4,解得a=.
∴抛物线的表达式为y=x2-x-4.
∴A(0,-4).
令y=0,解得xB=4.
∴B(4,0).
设直线AB为y=kx+b,将A、B点的坐标代入y=kx+b,得解得∴直线AB的函数表达式为y=x-4.
(2)连结EM,由条件可知∠OAB=∠OBA=45°.∵PF∥y轴,
∴∠EFP=45°.∴∠EMP=90°,∴∠EMF=90°.
∴劣弧EF的长为=·MF=·PF,
∴当PF最大时劣弧EF的弧长最大.
设点F(m,m-4),则点P(m,m2-m-4),其中0所以PF=m-4-=-m2+2m=-(m-2)2+2.
∴PF的最大值为2,∴劣弧EF长的最大值是.
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内 C.点P在⊙O上 D.无法确定
2.【教材P40练习T2变式】如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.给出下列四个结论,其中正确的结论为( )
A.三点确定一个圆 B.直径是最长的弦
C.圆周角是圆心角的一半 D.长度相等的弧是等弧
4.【2022·兰州】如图,△ABC内接于⊙O,CD是⊙O的直径,∠ACD=40°,则
∠B=( )
A.70° B.60° C.50° D.40°
5.【2022·自贡】P为⊙O外一点,PT与⊙O相切于点T,OP=10,∠OPT=30°,则PT长为( )
A.5 B.5 C.8 D.9
6.【2022·青岛一模】如图,在Rt△ABC中,∠C=90°,sin B=,AC=5 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相交 C.相切 D.相切或相交
7.【2022·清苑区一模】已知△ABC和△ABD有相同的外心,∠D=70°,则∠C的度数是( )
A.70° B.110° C.70°或110° D.不能确定
8.【教材P55习题T4改编】【2022·娄底】如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与三角形ABC的面积之比是( )
A. B. C. D.
9.已知一弧长为l的弧所对的圆心角为120°,那么它所对的弦长为( )
A.l B.l C.l D.l
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF,则线段EF长度的最小值为( )
A.2 B. C. D.3
二、填空题(每题3分,共24分)
11.【2022·内江】如图,在⊙O中,∠ABC=50°,则∠AOC等于________.
12.【2022·南京建邺区一模】如图,四边形ABCD内接于⊙O,若它的一个外角
∠DCE=122°,则另一个外角∠DAF=________.
13.【教材P49图27.2.6改编】如图,已知⊙O的半径为3,点O到直线l的距离OA=5,将直线l沿射线AO方向平移m个单位后,⊙O与直线l相切,则m=________.
14.直角三角形的两边长分别为16和12,则此直角三角形的外接圆的半径是________.
15.如图,PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,分别交PA、PB于点E、F.若∠APB=50°,则∠EOF的度数为________.
16.一个圆锥形漏斗,某同学测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
17.如图所示的网格中,每个小正方形的边长均为1,点A、B、D均在小正方形的顶点上,且点B、C在上, ∠BAC=22.5°,则的长为________cm.
18.中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,由此求得圆周率π的近似值.如图,设半径为r的圆内接正n边形的周长为C,圆的直径为d,当n=6时,π≈==3,则当n=12时,π≈≈________.(结果精确到0.01,参考数据:sin 15°=cos 75°≈0.259,sin 75°=cos 15°≈0.966)
三、解答题(19、20题每题10分,21、22题每题11分,23、24题每题12分,共66分)
19.【2022·怀化】如图,点A,B,C,D在⊙O上,=.求证:
(1)AC=BD;
(2)△ABE∽△DCE.
20.【教材P52练习T2变式】如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
21.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC、PD,切点分别为C、D,连结OP、CD.
(1)求证:OP⊥CD;
(2)连结AD、BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
22.如图,是一座拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱所在圆的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要通过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
23.【2022·滨州】如图,已知AC为⊙O的直径,直线PA与⊙O相切于点A,直线PD经过⊙O上的点B且∠CBD=∠CAB,连结OP交AB于点M.求证:
(1)PD是⊙O的切线;
(2)AM2=OM·PM.
24.如图①,已知抛物线y=ax2-x-4(a≠0)与y轴交于点A,与x轴交于点B、C,点C的坐标为(-2,0).
(1)求a的值和直线AB的函数表达式;
(2)如图②,连结AC,P是抛物线上一动点,且在直线AB的下方,过点P作y轴的平行线,交线段AB于点F,以PF为直径的⊙M与AB的另一个交点为E,连结PE.求劣弧EF长的最大值.
答案
一、1.A 2.D 3.B 4.C 5.A 6.A 7.C 8.A
9.C 点拨:设该弧所在⊙O的半径为r,所对的弦为AB.如图,过点O作OC⊥AB于点C.∵∠AOB=120°,∴的长为=l,则r=l.
∵∠AOB=120°,∴∠OBC=30°,∴OC=OB,
∴BC==l,∴AB=2BC=l.
10.C 点拨:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径
AD最短,连结OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=2,
∴AD=BD=2,即此时圆的直径为2,
由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OE·sin∠EOH=1×=,
∴EF=2EH=.
故选C.
二、11.100° 12.58° 13.2或8
14.8或10 15.65°
16.15π 17.
18.3.11 点拨:圆的内接正十二边形被半径分成12个如图所示的等腰三角形,
其顶角为30°.作OH⊥AB于点H,则∠AOH=15°.∵AO=BO=r,
∴在Rt△AOH中,sin∠AOH=,即sin 15°=,∴AH=r×sin 15°,
∴AB=2AH=2r×sin 15°,∴C=12×2r×sin 15°=24r×sin 15°.
又∵d=2r,∴π≈=≈3.11.
三、19.证明:(1)∵=,
∴=,
∴AC=BD.
(2)∵∠A=∠D,∠B=∠C,
∴△ABE∽△DCE.
20.解:(1)∵AB是⊙O的直径,AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
21.(1)证明:连结OD、OC,∵PD、PC是⊙O的切线,
∴PD=PC.
∵OD=OC,∴P、O在CD的中垂线上,
∴OP⊥CD.
(2)解:∵OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°.
∵OD=OC,
∴△COD是等边三角形.
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP==.
22.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设桥拱所在圆的半径为r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱所在圆的半径为50米.
(2)这艘轮船能顺利通过.理由如下:
如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM.
易知DE⊥MN,
∴MD=30米,
∴DE==40米.
∵EF=EC-CF=30米,
∴DF=DE-EF=10米.
∵10米>9米,
∴这艘轮船能顺利通过.
23.证明:(1)连结OB,如图所示.
∵OB=OC,
∴∠OCB=∠OBC.
∵AC是⊙O的直径,
∴∠CBA=90°.
∴∠CAB+∠OCB=90°.
∵∠CBD=∠CAB,
∴∠CBD+∠OBC=90°.
∴∠OBD=90°.
又∵OB是⊙O的半径,
∴PD是⊙O的切线.
(2)由PD是⊙O的切线,直线PA与⊙O相切,易得PO垂直平分AB.
∴∠AMP=∠AMO=90°.
∴∠APM+∠PAM=90°.
∵∠OAP=90°,
∴∠PAM+∠OAM=90°.
∴∠APM=∠OAM.
∴△OAM∽△APM.
∴=.
∴AM2=OM·PM.
24.解:(1)把C(-2,0)的坐标代入抛物线y=ax2-x-4(a≠0),
即0=a×(-2)2-(-2)-4,解得a=.
∴抛物线的表达式为y=x2-x-4.
∴A(0,-4).
令y=0,解得xB=4.
∴B(4,0).
设直线AB为y=kx+b,将A、B点的坐标代入y=kx+b,得解得∴直线AB的函数表达式为y=x-4.
(2)连结EM,由条件可知∠OAB=∠OBA=45°.∵PF∥y轴,
∴∠EFP=45°.∴∠EMP=90°,∴∠EMF=90°.
∴劣弧EF的长为=·MF=·PF,
∴当PF最大时劣弧EF的弧长最大.
设点F(m,m-4),则点P(m,m2-m-4),其中0
∴PF的最大值为2,∴劣弧EF长的最大值是.
