2022-2023学年华东师大版七年级数学上册 4.4平面图形 课时练习 (含答案)
文档属性
| 名称 | 2022-2023学年华东师大版七年级数学上册 4.4平面图形 课时练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 18:30:39 | ||
图片预览




文档简介
4.4平面图形(附解析)
一、单选题(共10个小题)
1.下列图形中属于平面图形的是( )
A.长方体 B.圆柱 C.圆 D.球
2.如图所示的美丽图案是由我们所熟悉的哪些图形组成的( )
A.三角形和半圆 B.圆和四边形 C.圆和三角形 D.半圆和四边形
3.下面几种几何图形中,属于立体图形的是( )
①三角形 ②长方形 ③正方体 ④圆 ⑤圆柱
A.①②④ B.②③⑤ C.③④⑤ D.③⑤
4.如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿图中的虚线剪开,拼成如图的一座“小房子”,则图中阴影部分的面积是( )
A.4 B.8 C.16 D.32
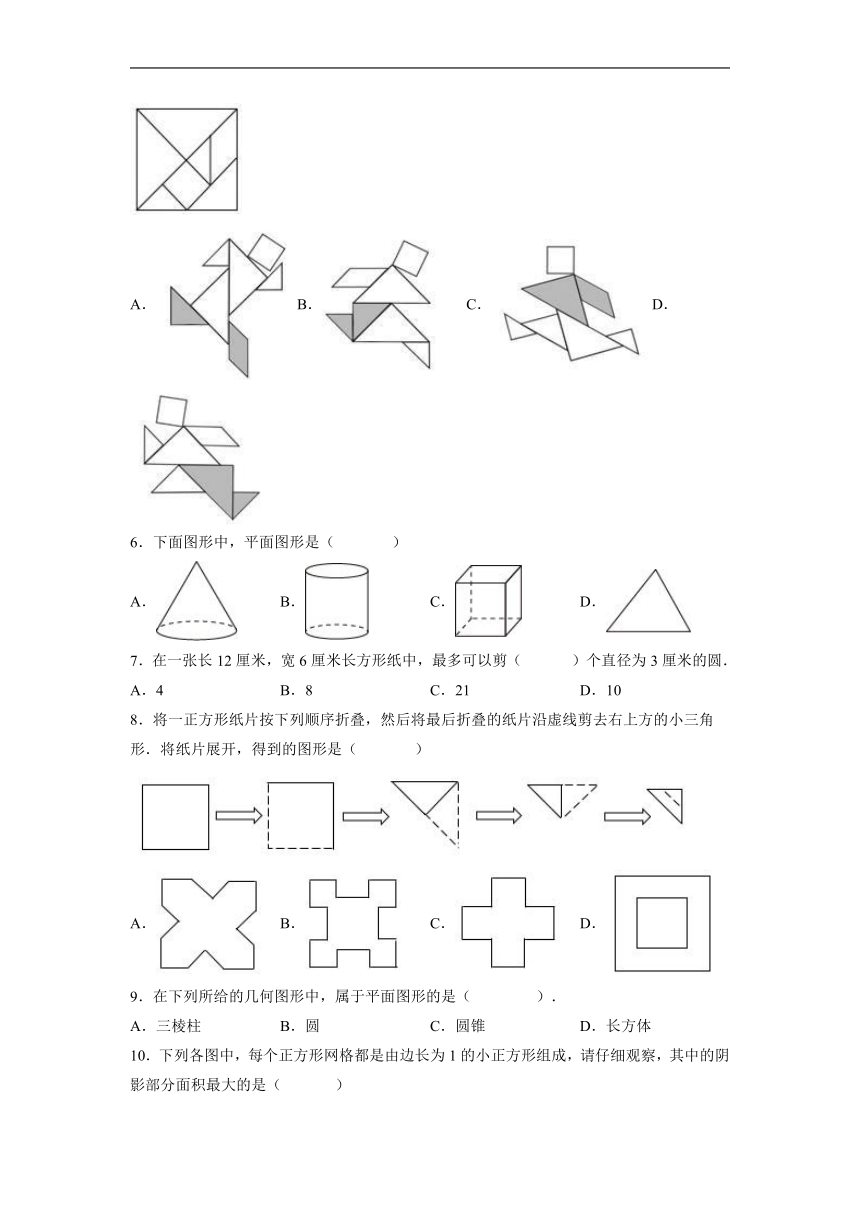
5.七巧板是古代中国劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,明、清两代在中国民间广泛流传,清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余,体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之,在一次数学活动课上,小明用边长为4cm的正方形纸板制作了如图所示的七巧板,并设计了下列四幅“奔跑者“作品,其中阴影部分的面积为5cm2的是( )
A.B.C.D.
6.下面图形中,平面图形是( )
A. B. C. D.
7.在一张长12厘米,宽6厘米长方形纸中,最多可以剪( )个直径为3厘米的圆.
A.4 B.8 C.21 D.10
8.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是( )
A. B. C. D.
9.在下列所给的几何图形中,属于平面图形的是( ).
A.三棱柱 B.圆 C.圆锥 D.长方体
10.下列各图中,每个正方形网格都是由边长为1的小正方形组成,请仔细观察,其中的阴影部分面积最大的是( )
A. B. C. D.
二、填空题(共10个小题)
11.一张圆形桌子的半径是0.5米,它的周长是_____米.
12.如图是小明同学为班级报刊《学习园地》设计的图案,则图中的平面图形有________、________、___________.(至少写出三种)
13.在如图的四个图形中,是平面图形的有_________(请填序号).
14.如图所示,图中共有______个长方形.
15.几何图形中,像直线、角、三角形、圆等,它们上面的各点都在____平面内,这样的图形叫做____.
16.在学校的综合实践课中,小双和小语同学利用一块边长为6cm的正方形纸板(如图①),制作了一朵芙蓉花(如图②),她们先将正方形纸板用虚线划分成36个全等的小正方形,再按其中的实线分割或七块形状不完全相同的图片并涂上不同颜色,制作成一副七巧板,最后用这副七巧板拼成了一朵芙蓉花,请问图②芙蓉花中阴影部分的面积占整朵芙蓉花面积的_________(不计重合部分).
17.2022年是农历虎年,小美利用一副七巧板拼出如图所示的“老虎”.已知左侧七巧板拼成的大正方形边长是4,则右侧“老虎”的虎头小正方形的面积是_____________.
18.把一幅七巧板按如图所示方式进行编号,①~⑦号分别对应着七巧板的七块.如果编号⑤的面积比编号③的面积小6,则由这幅七巧板拼得的“天鹅”的面积为_________.
19.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为___________.
20.把边长为2的正方形纸片ABCD分割成如图的四块,其中点E,F分别是AB,AD的中点,,,用这四块纸片拼成一个与正方形ABCD不重合的长方形MNPQ(要求这四块纸片不重叠无缝隙),则长方形MNPQ的周长是_________.
三、解答题(共3个小题)
21.一个六棱柱模型如所示,它的底面边长都是6cm,侧棱长4cm,观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面的面积之和是多少?
22.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
23.阅读材料
在房屋建造的过程中,我们常会见到“容积率”这个名词.“容积率”(floorarearatio),是指规划建设用地地面上的建筑物总面积与规划建设用地面积之比,其结果一般用整数或小数表示,比如一块规划建设用地面积为10000平方米,其中底层总面积为3000平方米,除底层之外其余楼层的总面积为22000平方米,那么这块规划建设用地的“容积率”就是=2.5,居住小区的“容积率”一般不超过5,因为规划建设用地的“容积率”越大,就意味着地面上建筑物的总面大,那么居住的人口也相对越多,会降低居民在小区内居住的舒适度.
(1)下列关于“容积率”的表述,错误的为 .
A.当规划建设用地面积确定时,地面上的建筑物总面积越大,容积率也越大
B.当地面的上建筑物总面积确定时,规划建设用地面积越大,容积率也越大
C.房产开发商希望容积率越大越,可出售的面积也越大,收益也越多
D.住户希望容积率越小越好,这样绿化、公共设施相对较多,小区环境就好
(2)某建筑规划建设用地6400平方米,该建筑的底层总面积为2240平方米,如果该建筑共10层,2至10层每层建筑面积均为1800平方米,那么建筑的容积率为多少?(精确到0.01)
(3)①某综合养老社区平面设计方案如图所示,阴影部分的面积为该建筑的底层面积,其中正方形AOGD与正方形OBCG的边长均为60米,OE、OF为120米,求该建筑的底层面积.
②若该养老社区规划建设用地面积为25000平方米,容积率为1.2,计划建造5层,且2至5层面积相同.为让老人居住舒适,平均每个床位需要12平方米的空间,且底层不安排床位,那么该养老社区总共可以安排多少个床位?
4.4平面图形解析
1.
【答案】C
【详解】平面图形是存在于一个平面上的图形
长方体:立体图形;
圆柱:立体图形;
圆:平面图形;
球:立体图形;
故选C
2.
【答案】A
【详解】解:观察图案可知,这个美丽的图案是由半圆和三角形组成,
故选:A.
3.
【答案】D
【详解】解:①三角形 , ②长方形 ,④圆,是平面图形; ③正方体,⑤圆柱,是立体图形.
综上,正确的有③⑤ .
故选:D.
4.
【答案】A
【详解】解:阴影部分由一个等腰直角三角形和一个直角梯形组成,
由第一个图形可知:阴影部分的两部分可构成正方形的四分之一,
正方形的面积=4×4=16,
∴图中阴影部分的面积是16÷4=4.
故选:A.
5.
【答案】D
【详解】解:∵正方形的边长为4cm,
∴七巧板中两个大等腰直角三角形的面积为4cm2,两个小等腰直角三角形的面积为1cm2,小正方形和平行四边形的面积为2cm2,右下角的等腰直角三角形的面积为2cm2,则
A中阴影部分面积和为4cm2,
B中阴影部分面积和为3cm2,
C中阴影部分面积和为6cm2,
D中阴影部分面积和为5cm2,
故选:D.
6.
【答案】D
【详解】解:解:根据平面图形的含义可知D为平面图形
故选D.
7.
【答案】B
【详解】(12÷3)×(6÷3),
=4×2,
=8(个),
故选:B.
8.
【答案】A
【详解】解:易得剪去的4个小正方形正好两两位于原正方形一组对边的中间.
故选A.
9.
【答案】B
【详解】解:三菱柱、圆锥和长方体都属于立体图形,圆属于平面图形.
故选:B.
10.
【答案】D
【详解】选项A中的阴影部分面积等于2,
选项B中的阴影部分面积等于4--2=,
选项C中的阴影部分面积等于2,
选项D中的阴影部分面积等于1++1= ,
综上,只有选项D符合题意.
故选D.
11.
【答案】
【详解】解:由题意得:圆的周长=2×0.5=(米),
故答案为:.
12.
【答案】 圆 三角形 正方形(答案不唯一)
【详解】解:观察图形可知:图中平面图形有圆、三角形、正方形、线段等.
故答案为:圆,三角形,正方形.
13.
【答案】①④
【详解】解:①④是平面图形,②③是立体几何,
故答案为①④.
14.
【答案】10
【详解】解:长方形是由线段构成,竖向都只有一条线段,横向线段AE上有5个分点(包括端点),每两点有一线段,有一线段得一个长方形,有几条线段就有几个长方形,
所以,长的一边AE上不同的线段共有1+2+3+4=10(条).
所以共有长方形10个.
故答案为:10.
15.
【答案】 同一 平面图形
【详解】几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一平面内,那么这样的几何图形叫做平面图形.
故答案为同一;平面图形.
16.
【答案】
【详解】解:由题意得可知②中的阴影部分的面积即①中实线围成的小正方形面积,
∵①中实线小正方形包含了2个完整的虚线小正方形,4个小正方形的一半,2个小正方形的,
∴①中实线小正方形的 面积为4.5个虚线小正方形,
∴图②芙蓉花中阴影部分的面积占整朵芙蓉花面积的,
故答案为:.
17.
【答案】2
【详解】解:大正方形的面积为4×4=16,
虎头小正方形的面积为
故答案为:2.
18.
【答案】32
【详解】解:设编号⑤对应的面积等于,编号③对应的面积等于,
编号⑤的面积比编号③的面积小6,
,
,
∴这幅七巧板拼得的“天鹅”的面积等于.
故答案为:.
19.
【答案】60°
【详解】分析:利用题目中所给的圆心角的度数之比去乘360°,从而可求得各个扇形的圆心角的度数.
详解:由题意可得,三个圆心角的和为360°,
又因为三个圆心角的度数比为1∶2∶3,
所以最小的圆心角度数为:.
故答案为60°.
20.
【答案】10
【详解】∵点E,F分别是AB,AD的中点,,
∴如下图,将三角形和四边形移动位置,即可得到长方形MNPQ;
∵正方形纸片ABCD边长为2
结合题意,得,
∴
∴长方形MNPQ的周长
故答案为:10.
21.
【答案】(1)2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;;(2)144cm2
【详解】(1)这个六棱柱有8个面,其中2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;
(2)解法一:其侧面积=六棱柱正视图面积×3
六棱柱正视图是三个长方形组成的大长方形,长为12cm,宽为4cm
六棱柱正视图的面积为12×4=48cm2
其侧面积=六棱柱正视图面积×3=48×3=144cm2.
答:这个六棱柱的所有侧面的面积之和为144cm2.
解法二:其侧面积为:6×4×6=144(m2).
答:这个六棱柱的所有侧面的面积之和为144cm2.
22.
【答案】(1)π,2π,π;(2)两个月牙形的面积之和等于三角形ABC的面积,理由见解析
【详解】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
设四个月牙的面积依次为S1,S2,S3,S4,如图,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径
SAB为直径=S2+S4+S△ABC,
又由(1)可得:∴SAB为直径=SAC为直径+SBC为直径=π,
S1+S2+S3+S4=S2+S4+S△ABC
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
23.
【答案】(1)B;(2)2.88;(3)①11808平方米;②1516个
【详解】解:(1)A.当规划建设用地面积确定时,地面上的建筑物总面积越大,容积率也越大,正确,选项不合题意;
B.当地面的上建筑物总面积确定时,规划建设用地面积越大,容积率也越小,故错误,选项符合题意;
C.房产开发商希望容积率越大越,可出售的面积也越大,收益也越多,故正确,选项不合题意;
D.住户希望容积率越小越好,这样绿化、公共设施相对较多,小区环境就好,故正确,选项不合题意;
故答案为:B;
(2)建筑的容积率==2.88;
(3)①如图,
在正方形OBCG中阴影部分的面积=扇形GOC的面积+扇形OBC的面积-正方形OBCG的面积
=(a+c+d)+(b+d+c)-(a+b+c+d)
=c+d
=2d,
而扇形GOC的面积=扇形BOC的面积==2826(平方米)
正方形OBCG的面积=60×60=3600(平方米)
扇形OEF的面积=(平方米)
则a的面积为3600-2826=774(平方米)
2Sd=2826×2-3600=2052(平方米)
∴S阴影=S扇形OEF-2Sa+2Sd=11304-774×2+2052=11808(平方米)
②25000×1.2=30000(平方米),
×4=1516(个),
答:该养老社区总共可以安排1516个床位.
一、单选题(共10个小题)
1.下列图形中属于平面图形的是( )
A.长方体 B.圆柱 C.圆 D.球
2.如图所示的美丽图案是由我们所熟悉的哪些图形组成的( )
A.三角形和半圆 B.圆和四边形 C.圆和三角形 D.半圆和四边形
3.下面几种几何图形中,属于立体图形的是( )
①三角形 ②长方形 ③正方体 ④圆 ⑤圆柱
A.①②④ B.②③⑤ C.③④⑤ D.③⑤
4.如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿图中的虚线剪开,拼成如图的一座“小房子”,则图中阴影部分的面积是( )
A.4 B.8 C.16 D.32
5.七巧板是古代中国劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,明、清两代在中国民间广泛流传,清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余,体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之,在一次数学活动课上,小明用边长为4cm的正方形纸板制作了如图所示的七巧板,并设计了下列四幅“奔跑者“作品,其中阴影部分的面积为5cm2的是( )
A.B.C.D.
6.下面图形中,平面图形是( )
A. B. C. D.
7.在一张长12厘米,宽6厘米长方形纸中,最多可以剪( )个直径为3厘米的圆.
A.4 B.8 C.21 D.10
8.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是( )
A. B. C. D.
9.在下列所给的几何图形中,属于平面图形的是( ).
A.三棱柱 B.圆 C.圆锥 D.长方体
10.下列各图中,每个正方形网格都是由边长为1的小正方形组成,请仔细观察,其中的阴影部分面积最大的是( )
A. B. C. D.
二、填空题(共10个小题)
11.一张圆形桌子的半径是0.5米,它的周长是_____米.
12.如图是小明同学为班级报刊《学习园地》设计的图案,则图中的平面图形有________、________、___________.(至少写出三种)
13.在如图的四个图形中,是平面图形的有_________(请填序号).
14.如图所示,图中共有______个长方形.
15.几何图形中,像直线、角、三角形、圆等,它们上面的各点都在____平面内,这样的图形叫做____.
16.在学校的综合实践课中,小双和小语同学利用一块边长为6cm的正方形纸板(如图①),制作了一朵芙蓉花(如图②),她们先将正方形纸板用虚线划分成36个全等的小正方形,再按其中的实线分割或七块形状不完全相同的图片并涂上不同颜色,制作成一副七巧板,最后用这副七巧板拼成了一朵芙蓉花,请问图②芙蓉花中阴影部分的面积占整朵芙蓉花面积的_________(不计重合部分).
17.2022年是农历虎年,小美利用一副七巧板拼出如图所示的“老虎”.已知左侧七巧板拼成的大正方形边长是4,则右侧“老虎”的虎头小正方形的面积是_____________.
18.把一幅七巧板按如图所示方式进行编号,①~⑦号分别对应着七巧板的七块.如果编号⑤的面积比编号③的面积小6,则由这幅七巧板拼得的“天鹅”的面积为_________.
19.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为___________.
20.把边长为2的正方形纸片ABCD分割成如图的四块,其中点E,F分别是AB,AD的中点,,,用这四块纸片拼成一个与正方形ABCD不重合的长方形MNPQ(要求这四块纸片不重叠无缝隙),则长方形MNPQ的周长是_________.
三、解答题(共3个小题)
21.一个六棱柱模型如所示,它的底面边长都是6cm,侧棱长4cm,观察这个模型,回答下列问题:
(1)这个六棱柱的几个面分别是什么形状?哪些面的形状、大小完全相同?
(2)这个六棱柱的所有侧面的面积之和是多少?
22.有一个著名的希波克拉蒂月牙问题.如图:以AB为直径作半圆,C是圆弧上一点,(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙形1、2(阴影部分).已知直径AC为4,直径BC为3,直径AB为5.
(1)分别求出三个半圆的面积(结果保留π);
(2)请你猜测,这两个月牙形的面积与三角形ABC的面积之间有何等量关系,请写出你的猜想,并通过计算说明.
23.阅读材料
在房屋建造的过程中,我们常会见到“容积率”这个名词.“容积率”(floorarearatio),是指规划建设用地地面上的建筑物总面积与规划建设用地面积之比,其结果一般用整数或小数表示,比如一块规划建设用地面积为10000平方米,其中底层总面积为3000平方米,除底层之外其余楼层的总面积为22000平方米,那么这块规划建设用地的“容积率”就是=2.5,居住小区的“容积率”一般不超过5,因为规划建设用地的“容积率”越大,就意味着地面上建筑物的总面大,那么居住的人口也相对越多,会降低居民在小区内居住的舒适度.
(1)下列关于“容积率”的表述,错误的为 .
A.当规划建设用地面积确定时,地面上的建筑物总面积越大,容积率也越大
B.当地面的上建筑物总面积确定时,规划建设用地面积越大,容积率也越大
C.房产开发商希望容积率越大越,可出售的面积也越大,收益也越多
D.住户希望容积率越小越好,这样绿化、公共设施相对较多,小区环境就好
(2)某建筑规划建设用地6400平方米,该建筑的底层总面积为2240平方米,如果该建筑共10层,2至10层每层建筑面积均为1800平方米,那么建筑的容积率为多少?(精确到0.01)
(3)①某综合养老社区平面设计方案如图所示,阴影部分的面积为该建筑的底层面积,其中正方形AOGD与正方形OBCG的边长均为60米,OE、OF为120米,求该建筑的底层面积.
②若该养老社区规划建设用地面积为25000平方米,容积率为1.2,计划建造5层,且2至5层面积相同.为让老人居住舒适,平均每个床位需要12平方米的空间,且底层不安排床位,那么该养老社区总共可以安排多少个床位?
4.4平面图形解析
1.
【答案】C
【详解】平面图形是存在于一个平面上的图形
长方体:立体图形;
圆柱:立体图形;
圆:平面图形;
球:立体图形;
故选C
2.
【答案】A
【详解】解:观察图案可知,这个美丽的图案是由半圆和三角形组成,
故选:A.
3.
【答案】D
【详解】解:①三角形 , ②长方形 ,④圆,是平面图形; ③正方体,⑤圆柱,是立体图形.
综上,正确的有③⑤ .
故选:D.
4.
【答案】A
【详解】解:阴影部分由一个等腰直角三角形和一个直角梯形组成,
由第一个图形可知:阴影部分的两部分可构成正方形的四分之一,
正方形的面积=4×4=16,
∴图中阴影部分的面积是16÷4=4.
故选:A.
5.
【答案】D
【详解】解:∵正方形的边长为4cm,
∴七巧板中两个大等腰直角三角形的面积为4cm2,两个小等腰直角三角形的面积为1cm2,小正方形和平行四边形的面积为2cm2,右下角的等腰直角三角形的面积为2cm2,则
A中阴影部分面积和为4cm2,
B中阴影部分面积和为3cm2,
C中阴影部分面积和为6cm2,
D中阴影部分面积和为5cm2,
故选:D.
6.
【答案】D
【详解】解:解:根据平面图形的含义可知D为平面图形
故选D.
7.
【答案】B
【详解】(12÷3)×(6÷3),
=4×2,
=8(个),
故选:B.
8.
【答案】A
【详解】解:易得剪去的4个小正方形正好两两位于原正方形一组对边的中间.
故选A.
9.
【答案】B
【详解】解:三菱柱、圆锥和长方体都属于立体图形,圆属于平面图形.
故选:B.
10.
【答案】D
【详解】选项A中的阴影部分面积等于2,
选项B中的阴影部分面积等于4--2=,
选项C中的阴影部分面积等于2,
选项D中的阴影部分面积等于1++1= ,
综上,只有选项D符合题意.
故选D.
11.
【答案】
【详解】解:由题意得:圆的周长=2×0.5=(米),
故答案为:.
12.
【答案】 圆 三角形 正方形(答案不唯一)
【详解】解:观察图形可知:图中平面图形有圆、三角形、正方形、线段等.
故答案为:圆,三角形,正方形.
13.
【答案】①④
【详解】解:①④是平面图形,②③是立体几何,
故答案为①④.
14.
【答案】10
【详解】解:长方形是由线段构成,竖向都只有一条线段,横向线段AE上有5个分点(包括端点),每两点有一线段,有一线段得一个长方形,有几条线段就有几个长方形,
所以,长的一边AE上不同的线段共有1+2+3+4=10(条).
所以共有长方形10个.
故答案为:10.
15.
【答案】 同一 平面图形
【详解】几何图形中,像直线、角、三角形、圆等,它们上面的各点都在同一平面内,那么这样的几何图形叫做平面图形.
故答案为同一;平面图形.
16.
【答案】
【详解】解:由题意得可知②中的阴影部分的面积即①中实线围成的小正方形面积,
∵①中实线小正方形包含了2个完整的虚线小正方形,4个小正方形的一半,2个小正方形的,
∴①中实线小正方形的 面积为4.5个虚线小正方形,
∴图②芙蓉花中阴影部分的面积占整朵芙蓉花面积的,
故答案为:.
17.
【答案】2
【详解】解:大正方形的面积为4×4=16,
虎头小正方形的面积为
故答案为:2.
18.
【答案】32
【详解】解:设编号⑤对应的面积等于,编号③对应的面积等于,
编号⑤的面积比编号③的面积小6,
,
,
∴这幅七巧板拼得的“天鹅”的面积等于.
故答案为:.
19.
【答案】60°
【详解】分析:利用题目中所给的圆心角的度数之比去乘360°,从而可求得各个扇形的圆心角的度数.
详解:由题意可得,三个圆心角的和为360°,
又因为三个圆心角的度数比为1∶2∶3,
所以最小的圆心角度数为:.
故答案为60°.
20.
【答案】10
【详解】∵点E,F分别是AB,AD的中点,,
∴如下图,将三角形和四边形移动位置,即可得到长方形MNPQ;
∵正方形纸片ABCD边长为2
结合题意,得,
∴
∴长方形MNPQ的周长
故答案为:10.
21.
【答案】(1)2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;;(2)144cm2
【详解】(1)这个六棱柱有8个面,其中2个相同底面是边长为6cm的正六边形,6个相同侧面是长为6m,宽为4m的长方形;
(2)解法一:其侧面积=六棱柱正视图面积×3
六棱柱正视图是三个长方形组成的大长方形,长为12cm,宽为4cm
六棱柱正视图的面积为12×4=48cm2
其侧面积=六棱柱正视图面积×3=48×3=144cm2.
答:这个六棱柱的所有侧面的面积之和为144cm2.
解法二:其侧面积为:6×4×6=144(m2).
答:这个六棱柱的所有侧面的面积之和为144cm2.
22.
【答案】(1)π,2π,π;(2)两个月牙形的面积之和等于三角形ABC的面积,理由见解析
【详解】解:(1)以AB为直径的半圆:
SAB为直径=π×()2=π,
以AC为直径的半圆:
SAC为直径=π×22=2π,
以BC为直径的半圆:
SBC为直径=π×()2=π,
(2)两个月牙形的面积之和等于三角形ABC的面积.
设四个月牙的面积依次为S1,S2,S3,S4,如图,
于是,S1+S2=SBC为直径=π,S3+S4=SBC为直径=2π,
∴S1+S2+S3+S4=SBC为直径+SBC为直径
SAB为直径=S2+S4+S△ABC,
又由(1)可得:∴SAB为直径=SAC为直径+SBC为直径=π,
S1+S2+S3+S4=S2+S4+S△ABC
∴S1+S3=S△ABC,
即:两个月牙形的面积之和等于三角形ABC的面积.
23.
【答案】(1)B;(2)2.88;(3)①11808平方米;②1516个
【详解】解:(1)A.当规划建设用地面积确定时,地面上的建筑物总面积越大,容积率也越大,正确,选项不合题意;
B.当地面的上建筑物总面积确定时,规划建设用地面积越大,容积率也越小,故错误,选项符合题意;
C.房产开发商希望容积率越大越,可出售的面积也越大,收益也越多,故正确,选项不合题意;
D.住户希望容积率越小越好,这样绿化、公共设施相对较多,小区环境就好,故正确,选项不合题意;
故答案为:B;
(2)建筑的容积率==2.88;
(3)①如图,
在正方形OBCG中阴影部分的面积=扇形GOC的面积+扇形OBC的面积-正方形OBCG的面积
=(a+c+d)+(b+d+c)-(a+b+c+d)
=c+d
=2d,
而扇形GOC的面积=扇形BOC的面积==2826(平方米)
正方形OBCG的面积=60×60=3600(平方米)
扇形OEF的面积=(平方米)
则a的面积为3600-2826=774(平方米)
2Sd=2826×2-3600=2052(平方米)
∴S阴影=S扇形OEF-2Sa+2Sd=11304-774×2+2052=11808(平方米)
②25000×1.2=30000(平方米),
×4=1516(个),
答:该养老社区总共可以安排1516个床位.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
