2022—2023学年人教版数学八年级上册 12.1 全等三角形 课堂提升训练 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 12.1 全等三角形 课堂提升训练 (含答案) | 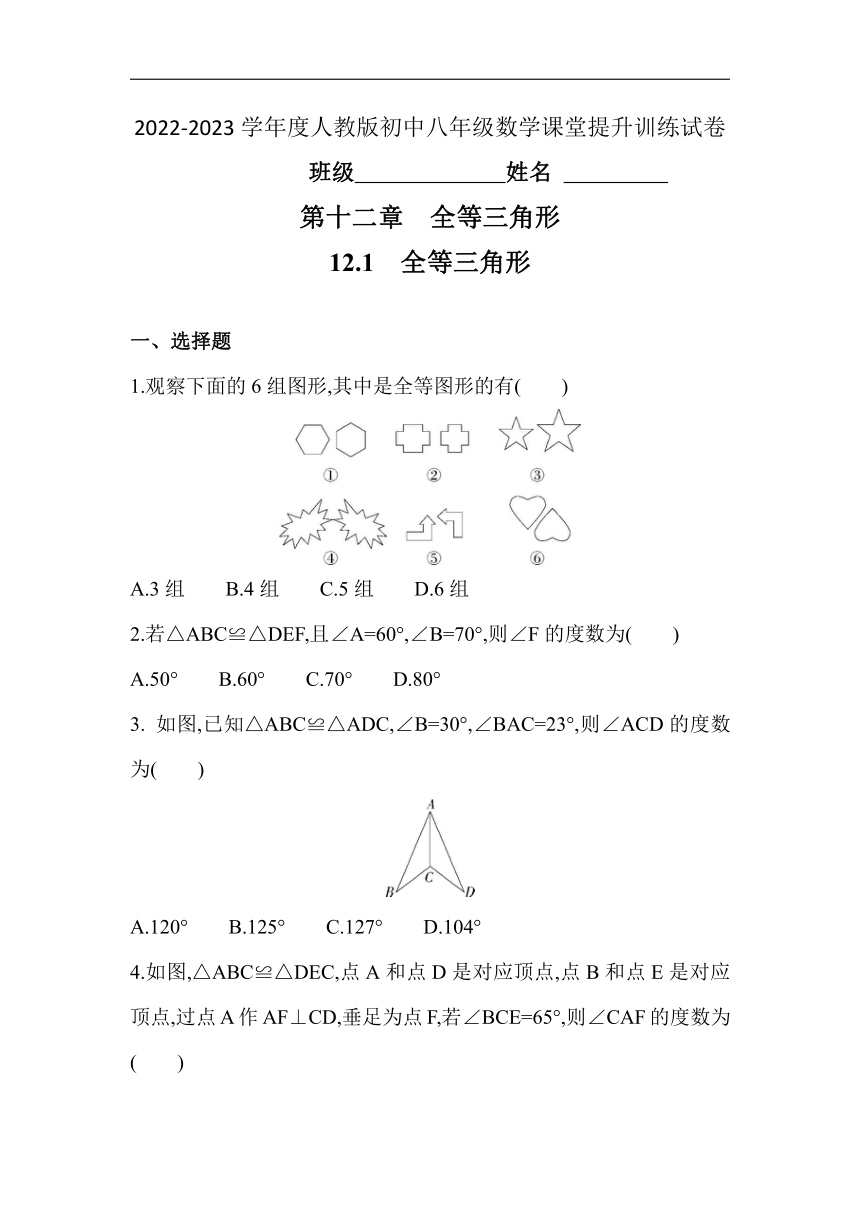 | |
| 格式 | docx | ||
| 文件大小 | 216.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 18:46:59 | ||
图片预览




文档简介
2022-2023学年度人教版初中八年级数学课堂提升训练试卷
班级 姓名
第十二章 全等三角形
12.1 全等三角形
一、选择题
1.观察下面的6组图形,其中是全等图形的有( )
A.3组 B.4组 C.5组 D.6组
2.若△ABC≌△DEF,且∠A=60°,∠B=70°,则∠F的度数为( )
A.50° B.60° C.70° D.80°
3. 如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120° B.125° C.127° D.104°
4.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
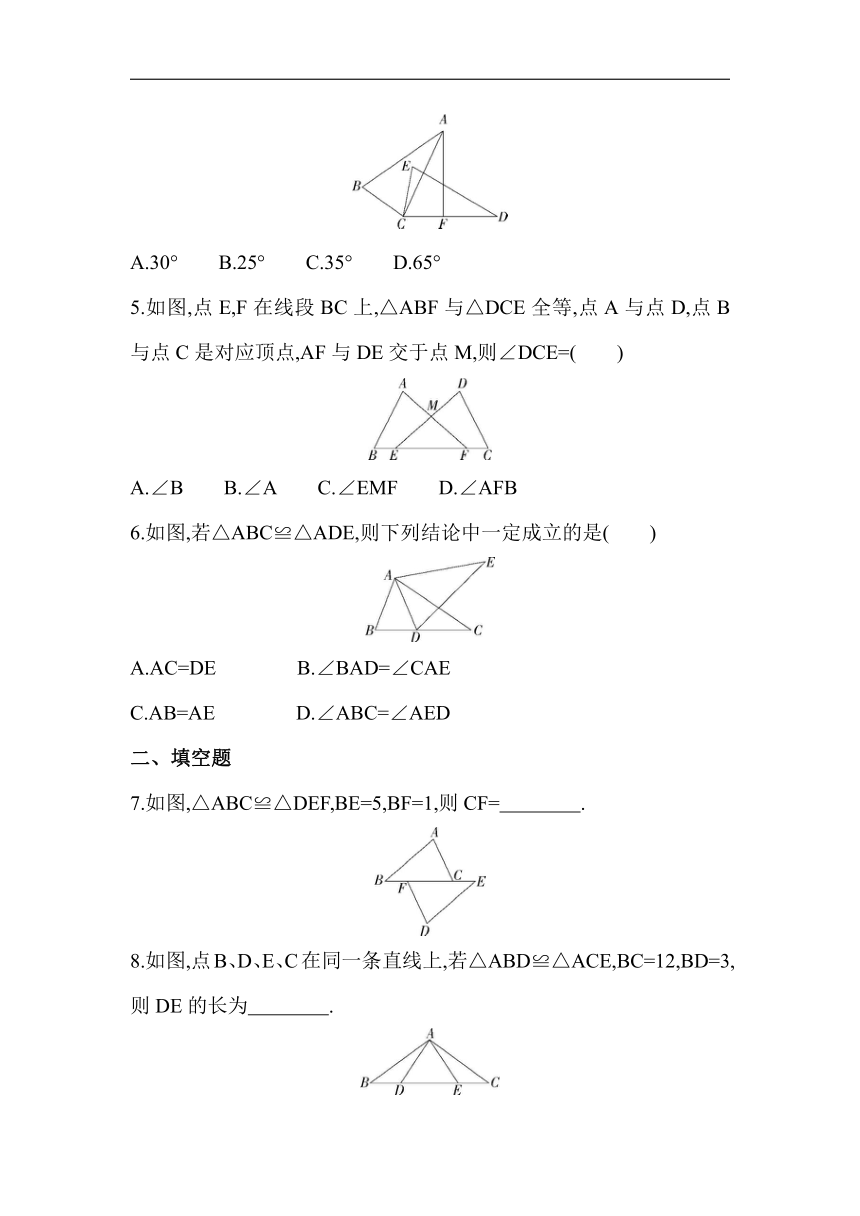
5.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
6.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
二、填空题
7.如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
8.如图,点B、D、E、C在同一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
9.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
10.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限内,且△ABD与△ABC全等,则点D的坐标是 .
三、解答题
11.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
12.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
13.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF;
(2)求AB的长.
14.如图,点A、B、C在同一条直线上,点E在BD上,且△ABD≌△EBC,AB=2 cm,BC=3 cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.
答案全解全析
一、选择题
1. 答案 B 观察题图,①④⑤⑥四组图形经过平移、旋转、对折后能够完全重合,是全等图形,故选B.
2.答案 A ∵∠A=60°,∠B=70°,
∴∠C=180°-60°-70°=50°,
∵△ABC≌△DEF,
∴∠F=∠C=50°.
3.答案 C ∵∠B=30°,∠BAC=23°,
∴∠ACB=180°-30°-23°=127°,
∵△ABC≌△ADC,
∴∠ACD=∠ACB=127°.
4. 答案 B ∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°-65°=25°,故选B.
5. 答案 A ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,
∴∠DCE=∠B,故选A.
6. 答案 B
∵△ABC≌△ADE,∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故A,C,D选项错误,B选项正确,故选B.
二、填空题
7.答案 3
解析 ∵BE=5,BF=1,
∴EF=BE-BF=4,
∵△ABC≌△DEF,
∴BC=EF=4,
∴CF=BC-BF=3.
8.答案 6
解析 ∵△ABD≌△ACE,BD=3,
∴CE=BD=3,
∵BC=12,
∴DE=BC-BD-CE=12-3-3=6.
故答案为6.
9.答案 13
解析 ∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30-AB-BC=13,
故答案为13.
10.答案 (-4,3)或(-4,2)
解析 如图,当△ABD≌△ABC时,点D的坐标是(-4,3),
当△ABD'≌△BAC时,点D'的坐标是(-4,2).
故点D的坐标是(-4,3)或(-4,2).
三、解答题
11.解析 (1)其他对应角为∠BAF和∠DCE,∠AFB和∠CED.
其他对应边为AB和CD,BF和DE.
(2)∵△ABF≌△CDE,∠B=30°,
∴∠D=∠B=30°,
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=30°+40°=70°.
(3)∵△ABF≌△CDE,∴BF=DE,
∴BF-EF=DE-EF,∴BE=DF,
∵BD=10,EF=2,∴DF=BE=4,∴BF=BE+EF=4+2=6.
12.解析 (1)∵BD⊥DE,∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,∴∠DBA=∠CAE,
∴∠BAD+∠CAE=90°,∴∠BAC=90°.
(2)∵△ABD≌△CAE,∴AB=AC=4,
∴△ABC的面积=×4×4=8.
13.解析 (1)证明:∵△ABC≌△FED,
∴∠A=∠F,∴AC∥DF.
(2)∵△ABC≌△FED,∴AB=EF,
∴AB-EB=EF-EB,∴AE=BF.
∵AF=8,BE=2,∴AE+BF=8-2=6,
∴AE=3,∴AB=AE+BE=3+2=5.
14.解析 (1)∵△ABD≌△EBC,∴BD=BC=3 cm,BE=AB=2 cm,
∴DE=BD-BE=1 cm.
(2)DB与AC垂直.
理由:∵△ABD≌△EBC,∴∠ABD=∠EBC,
又点A、B、C在同一条直线上,
∴∠EBC=∠ABD=90°,∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,∴∠D=∠C,
由(2)知∠ABD=90°,∴∠A+∠D=90°,
∴∠A+∠C=90°,∴∠AFC=90°,
∴直线AD与直线CE垂直.
班级 姓名
第十二章 全等三角形
12.1 全等三角形
一、选择题
1.观察下面的6组图形,其中是全等图形的有( )
A.3组 B.4组 C.5组 D.6组
2.若△ABC≌△DEF,且∠A=60°,∠B=70°,则∠F的度数为( )
A.50° B.60° C.70° D.80°
3. 如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120° B.125° C.127° D.104°
4.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30° B.25° C.35° D.65°
5.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
A.∠B B.∠A C.∠EMF D.∠AFB
6.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
二、填空题
7.如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
8.如图,点B、D、E、C在同一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为 .
9.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是 .
10.如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),点D在第二象限内,且△ABD与△ABC全等,则点D的坐标是 .
三、解答题
11.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
12.如图,D、A、E三点在同一条直线上,BD⊥DE于点D,CE⊥DE于点E,且△ABD≌△CAE,AC=4.
(1)求∠BAC的度数;
(2)求△ABC的面积.
13.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF;
(2)求AB的长.
14.如图,点A、B、C在同一条直线上,点E在BD上,且△ABD≌△EBC,AB=2 cm,BC=3 cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.
答案全解全析
一、选择题
1. 答案 B 观察题图,①④⑤⑥四组图形经过平移、旋转、对折后能够完全重合,是全等图形,故选B.
2.答案 A ∵∠A=60°,∠B=70°,
∴∠C=180°-60°-70°=50°,
∵△ABC≌△DEF,
∴∠F=∠C=50°.
3.答案 C ∵∠B=30°,∠BAC=23°,
∴∠ACB=180°-30°-23°=127°,
∵△ABC≌△ADC,
∴∠ACD=∠ACB=127°.
4. 答案 B ∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°-65°=25°,故选B.
5. 答案 A ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,
∴∠DCE=∠B,故选A.
6. 答案 B
∵△ABC≌△ADE,∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.故A,C,D选项错误,B选项正确,故选B.
二、填空题
7.答案 3
解析 ∵BE=5,BF=1,
∴EF=BE-BF=4,
∵△ABC≌△DEF,
∴BC=EF=4,
∴CF=BC-BF=3.
8.答案 6
解析 ∵△ABD≌△ACE,BD=3,
∴CE=BD=3,
∵BC=12,
∴DE=BC-BD-CE=12-3-3=6.
故答案为6.
9.答案 13
解析 ∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30-AB-BC=13,
故答案为13.
10.答案 (-4,3)或(-4,2)
解析 如图,当△ABD≌△ABC时,点D的坐标是(-4,3),
当△ABD'≌△BAC时,点D'的坐标是(-4,2).
故点D的坐标是(-4,3)或(-4,2).
三、解答题
11.解析 (1)其他对应角为∠BAF和∠DCE,∠AFB和∠CED.
其他对应边为AB和CD,BF和DE.
(2)∵△ABF≌△CDE,∠B=30°,
∴∠D=∠B=30°,
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=30°+40°=70°.
(3)∵△ABF≌△CDE,∴BF=DE,
∴BF-EF=DE-EF,∴BE=DF,
∵BD=10,EF=2,∴DF=BE=4,∴BF=BE+EF=4+2=6.
12.解析 (1)∵BD⊥DE,∴∠D=90°,
∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,∴∠DBA=∠CAE,
∴∠BAD+∠CAE=90°,∴∠BAC=90°.
(2)∵△ABD≌△CAE,∴AB=AC=4,
∴△ABC的面积=×4×4=8.
13.解析 (1)证明:∵△ABC≌△FED,
∴∠A=∠F,∴AC∥DF.
(2)∵△ABC≌△FED,∴AB=EF,
∴AB-EB=EF-EB,∴AE=BF.
∵AF=8,BE=2,∴AE+BF=8-2=6,
∴AE=3,∴AB=AE+BE=3+2=5.
14.解析 (1)∵△ABD≌△EBC,∴BD=BC=3 cm,BE=AB=2 cm,
∴DE=BD-BE=1 cm.
(2)DB与AC垂直.
理由:∵△ABD≌△EBC,∴∠ABD=∠EBC,
又点A、B、C在同一条直线上,
∴∠EBC=∠ABD=90°,∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,∴∠D=∠C,
由(2)知∠ABD=90°,∴∠A+∠D=90°,
∴∠A+∠C=90°,∴∠AFC=90°,
∴直线AD与直线CE垂直.
