2022—2023学年人教版数学八年级上册 13.3.2 等边三角形(第1课时) 课堂提升训练试卷 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 13.3.2 等边三角形(第1课时) 课堂提升训练试卷 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 311.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览



文档简介
2022-2023学年度人教版初中八年级数学课堂提升训练试卷
班级 姓名
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形第1课时
一、选择题
1.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论中:①点P在∠BAC的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP,正确的有( )
A.1个 B.2个 C.3个 D.4个
2. 如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC B.EF=FD C.BE=BD D.AE=AC
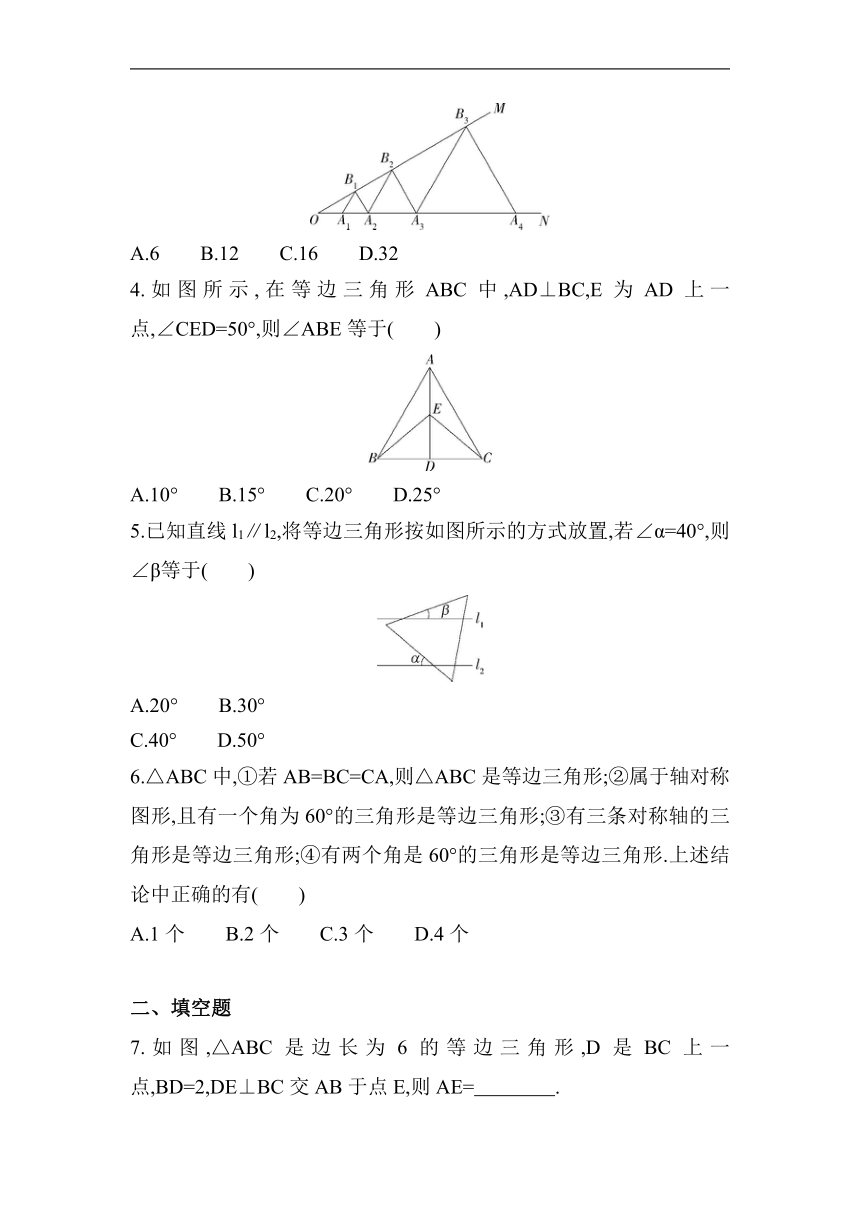
3.如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=,则△A6B6A7的边长为( )
A.6 B.12 C.16 D.32
4.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
5.已知直线l1∥l2,将等边三角形按如图所示的方式放置,若∠α=40°,则∠β等于( )
A.20° B.30°
C.40° D.50°
6.△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
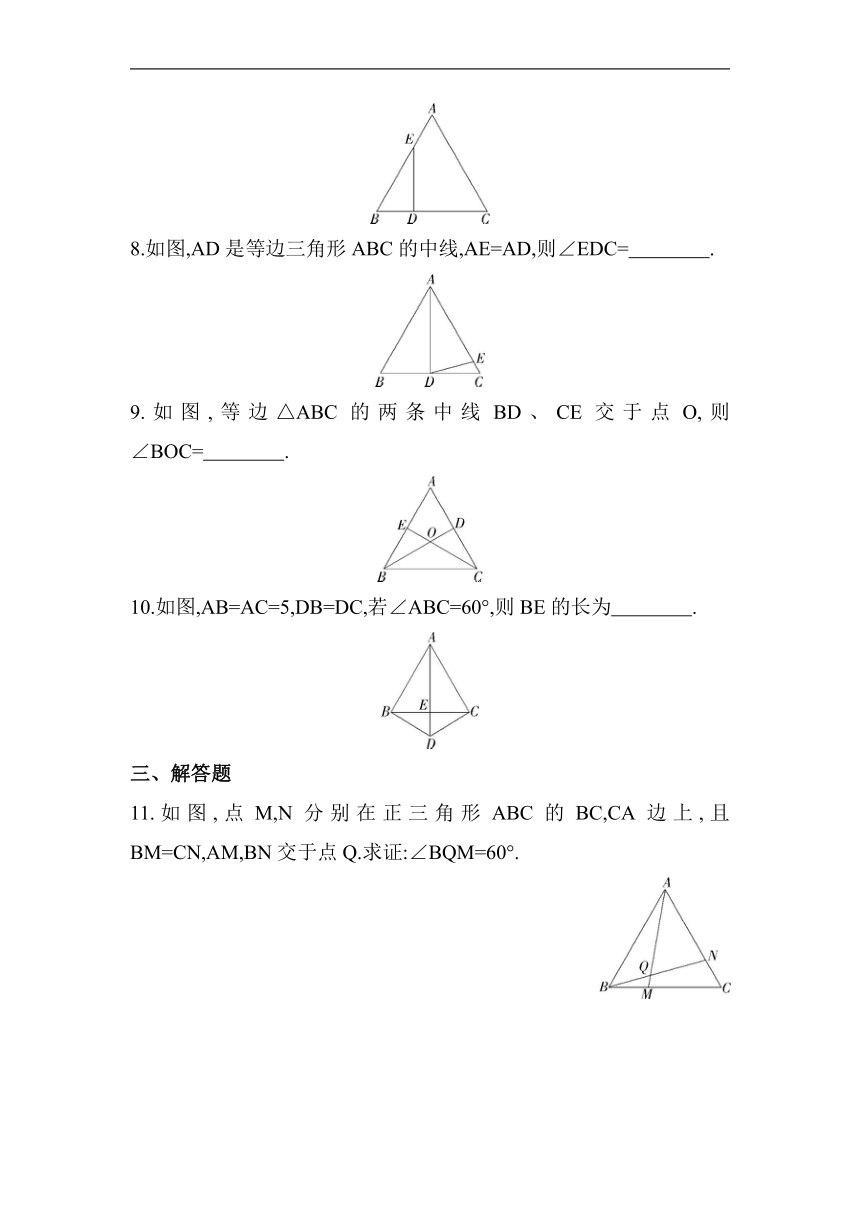
7.如图,△ABC是边长为6的等边三角形,D是BC上一点,BD=2,DE⊥BC交AB于点E,则AE= .
8.如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC= .
9.如图,等边△ABC的两条中线BD、CE交于点O,则∠BOC= .
10.如图,AB=AC=5,DB=DC,若∠ABC=60°,则BE的长为 .
三、解答题
11.如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60°.
12.如图所示,已知等边△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,已知点M的速度是1厘米/秒,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N运动几秒后重合
(2)M、N运动几秒后,可得到等边△AMN
(3)M、N在BC边上运动时,是否存在以MN为底边的等腰△AMN 如果存在,请求出此时M、N运动的时间;如果不存在,请说明理由.
13.如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使DB=DE.
(1)求∠BDE的度数;
(2)求证:△CED为等腰三角形.
14.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形 试说明你的结论.
答案全解全析
一、选择题
1.答案 D ∵PR⊥AB,PS⊥AC,且PR=PS,
∴点P在∠BAC的平分线上,故①正确;
∵△ABC为等边三角形,∴由①可得PB=PC,
∵∠B=∠C,∠BRP=∠CSP=90°,∴△BPR≌△CPS,∴BR=CS,
∵AB=AC,∴AS=AR,故②正确;
∵AQ=PQ,∴∠QAP=∠QPA,∴∠PQC=2∠PAC=∠BAC,∴QP∥AR,故③正确;
∵∠PQC=∠BAC=60°=∠C,∴△PQC是等边三角形,
∵PS⊥AC,∴△PQS≌△PCS,∴△BRP≌△QSP,故④正确.
∴正确的有4个.
2.答案 D ∵△ABC是等边三角形,△ADE是等边三角形,
∴AB=AC=BC,∠BAC=60°,AE=AD=ED,∠EAD=60°,
∵AD是△ABC的角平分线,∴∠DAB=∠DAC=30°,
∴AD⊥BC(A结论正确),∠EAB=30°=∠BAD,
∴AB⊥ED,EF=DF(B结论正确),∴BE=BD(C结论正确),
无法得出AE=AC,故D结论错误.
3.答案 C 如图,∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,
∵∠MON=30°,∴∠1=180°-120°-30°=30°,
又∵∠3=60°,∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,∴A1B1=OA1=,∴A2B1=,
∵△A2B2A3、△A3B3A4都是等边三角形,
∴∠11=∠10=∠13=60°,
∴∠4=∠10=∠11=∠3=∠13,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠6=∠7=∠1=30°,∠8=∠5=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,
……
∴△AnBnAn+1的边长为×2n-1,
∴△A6B6A7的边长为×26-1=×25=16.故选C.
4. 答案 C ∵△ABC为等边三角形,AD⊥BC,
∴AD所在直线是BC的垂直平分线,∠ABC=60°,
∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD,
∵∠CED=50°,∴∠ECD=40°,∴∠EBD=40°,
∴∠ABE=∠ABC-∠EBC=60°-40°=20°,故选C.
5. 答案 A 过点A作AD∥l1,如图,则∠BAD=∠β.
∵l1∥l2,∴AD∥l2,∴∠DAC=∠α=40°.
∵△ABC是等边三角形,∴∠BAC=60°,
∴∠β=∠BAD=∠BAC-∠DAC=60°-40°=20°.
故选A.
6. 答案 D ①三边相等的三角形是等边三角形,正确;
②属于轴对称图形,且有一个角为60°的三角形是等边三角形,正确;
③有三条对称轴的三角形是等边三角形,正确;
④有两个角是60°的三角形是等边三角形,正确.
故正确的有4个.故选D.
二、填空题
7.答案 2
解析 ∵△ABC是等边三角形,∴∠B=60°,
∵DE⊥BC,∴∠EDB=90°,∴∠BED=30°,∴BE=2BD,
∵BD=2,∴EB=2BD=4,∴AE=AB-BE=6-4=2,故答案为2.
8.答案 15°
解析 ∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,
∴∠ADC=90°,
∵AD=AE,∴∠ADE=∠AED==75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
9. 答案 120°
解析 ∵△ABC是等边三角形,BD、CE是中线,
∴BD⊥AC,∠ACE=∠ACB=30°,∴∠BDC=90°,
∴∠BOC=∠ODC+∠ACE=120°,故答案为120°.
10. 答案 2.5
解析 ∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,点A在BC的垂直平分线上,
∴BC=AB=5,
∵DB=DC,∴点D在BC的垂直平分线上,
∴AD垂直平分BC,∴BE=BC=2.5.
三、解答题
11.证明 ∵BM=CN,BC=AC,∴CM=AN,
又∵AB=AC,∠BAN=∠ACM=60°,∴△AMC≌△BNA,∴∠AMC=∠BNA,
∵∠MAN+∠ANB+∠AQN=180°,∠MAN+∠AMC+∠ACB=180°,∴∠AQN=∠ACB,
∵∠BQM=∠AQN,∴∠BQM=∠ACB=60°.
12.解析 (1)设点M、N运动x秒后重合,
由题意得x×1+10=2x,解得x=10,
故M、N运动10秒后重合.
(2)设点M、N运动t秒后,可得到等边△AMN,如图1,
易知AM=t×1=t厘米,AN=AB-BN=(10-2t)厘米,
∵△ABC为等边三角形,∴∠A=60°,
∵△AMN是等边三角形,∴AM=AN,即t=10-2t,解得t=,
∴点M、N运动秒后,可得到等边△AMN.
(3)当点M、N在BC边上运动时,存在以MN为底边的等腰△AMN.
由(1)知10秒时M、N两点重合,恰好在C处,
如图2,假设△AMN是等腰三角形,且AN=AM,
∴∠AMN=∠ANM,∴∠AMC=∠ANB,
∵△ABC是等边三角形,∴∠C=∠B,AC=AB,
在△ACM和△ABN中,
∴△ACM≌△ABN(AAS),∴CM=BN,
设当点M、N运动的时间为y秒时,△AMN是等腰三角形,
∴CM=(y-10)厘米,NB=(30-2y)厘米,∴y-10=30-2y,解得y=,故假设成立.
∴当点M、N在BC边上运动时,存在以MN为底边的等腰△AMN,此时M、N运动的时间为秒.
13.解析 (1)∵DB=DE,∴∠E=∠DBE,
∵△ABC是等边三角形,BD是AC边上的高,
∴∠DBC=30°,∴∠E=∠DBE=30°,
∴∠BDE=180°-30°-30°=120°.
(2)证明:∵△ABC是等边三角形,∴∠ACB=60°,
∵∠E=30°,∴∠CDE=∠ACB-∠E=30°,
∴∠CDE=∠E,∴CD=CE,
∴△CED是等腰三角形.
14.解析 △APQ为等边三角形.
证明:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
班级 姓名
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形第1课时
一、选择题
1.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论中:①点P在∠BAC的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP,正确的有( )
A.1个 B.2个 C.3个 D.4个
2. 如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论不正确的是( )
A.AD⊥BC B.EF=FD C.BE=BD D.AE=AC
3.如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=,则△A6B6A7的边长为( )
A.6 B.12 C.16 D.32
4.如图所示,在等边三角形ABC中,AD⊥BC,E为AD上一点,∠CED=50°,则∠ABE等于( )
A.10° B.15° C.20° D.25°
5.已知直线l1∥l2,将等边三角形按如图所示的方式放置,若∠α=40°,则∠β等于( )
A.20° B.30°
C.40° D.50°
6.△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
7.如图,△ABC是边长为6的等边三角形,D是BC上一点,BD=2,DE⊥BC交AB于点E,则AE= .
8.如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC= .
9.如图,等边△ABC的两条中线BD、CE交于点O,则∠BOC= .
10.如图,AB=AC=5,DB=DC,若∠ABC=60°,则BE的长为 .
三、解答题
11.如图,点M,N分别在正三角形ABC的BC,CA边上,且BM=CN,AM,BN交于点Q.求证:∠BQM=60°.
12.如图所示,已知等边△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,已知点M的速度是1厘米/秒,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N运动几秒后重合
(2)M、N运动几秒后,可得到等边△AMN
(3)M、N在BC边上运动时,是否存在以MN为底边的等腰△AMN 如果存在,请求出此时M、N运动的时间;如果不存在,请说明理由.
13.如图,△ABC是等边三角形,BD是AC边上的高,延长BC至E,使DB=DE.
(1)求∠BDE的度数;
(2)求证:△CED为等腰三角形.
14.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形 试说明你的结论.
答案全解全析
一、选择题
1.答案 D ∵PR⊥AB,PS⊥AC,且PR=PS,
∴点P在∠BAC的平分线上,故①正确;
∵△ABC为等边三角形,∴由①可得PB=PC,
∵∠B=∠C,∠BRP=∠CSP=90°,∴△BPR≌△CPS,∴BR=CS,
∵AB=AC,∴AS=AR,故②正确;
∵AQ=PQ,∴∠QAP=∠QPA,∴∠PQC=2∠PAC=∠BAC,∴QP∥AR,故③正确;
∵∠PQC=∠BAC=60°=∠C,∴△PQC是等边三角形,
∵PS⊥AC,∴△PQS≌△PCS,∴△BRP≌△QSP,故④正确.
∴正确的有4个.
2.答案 D ∵△ABC是等边三角形,△ADE是等边三角形,
∴AB=AC=BC,∠BAC=60°,AE=AD=ED,∠EAD=60°,
∵AD是△ABC的角平分线,∴∠DAB=∠DAC=30°,
∴AD⊥BC(A结论正确),∠EAB=30°=∠BAD,
∴AB⊥ED,EF=DF(B结论正确),∴BE=BD(C结论正确),
无法得出AE=AC,故D结论错误.
3.答案 C 如图,∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,
∵∠MON=30°,∴∠1=180°-120°-30°=30°,
又∵∠3=60°,∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,∴A1B1=OA1=,∴A2B1=,
∵△A2B2A3、△A3B3A4都是等边三角形,
∴∠11=∠10=∠13=60°,
∴∠4=∠10=∠11=∠3=∠13,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠6=∠7=∠1=30°,∠8=∠5=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,
……
∴△AnBnAn+1的边长为×2n-1,
∴△A6B6A7的边长为×26-1=×25=16.故选C.
4. 答案 C ∵△ABC为等边三角形,AD⊥BC,
∴AD所在直线是BC的垂直平分线,∠ABC=60°,
∵E是AD上一点,∴EB=EC,∴∠EBD=∠ECD,
∵∠CED=50°,∴∠ECD=40°,∴∠EBD=40°,
∴∠ABE=∠ABC-∠EBC=60°-40°=20°,故选C.
5. 答案 A 过点A作AD∥l1,如图,则∠BAD=∠β.
∵l1∥l2,∴AD∥l2,∴∠DAC=∠α=40°.
∵△ABC是等边三角形,∴∠BAC=60°,
∴∠β=∠BAD=∠BAC-∠DAC=60°-40°=20°.
故选A.
6. 答案 D ①三边相等的三角形是等边三角形,正确;
②属于轴对称图形,且有一个角为60°的三角形是等边三角形,正确;
③有三条对称轴的三角形是等边三角形,正确;
④有两个角是60°的三角形是等边三角形,正确.
故正确的有4个.故选D.
二、填空题
7.答案 2
解析 ∵△ABC是等边三角形,∴∠B=60°,
∵DE⊥BC,∴∠EDB=90°,∴∠BED=30°,∴BE=2BD,
∵BD=2,∴EB=2BD=4,∴AE=AB-BE=6-4=2,故答案为2.
8.答案 15°
解析 ∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,
∴∠ADC=90°,
∵AD=AE,∴∠ADE=∠AED==75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
9. 答案 120°
解析 ∵△ABC是等边三角形,BD、CE是中线,
∴BD⊥AC,∠ACE=∠ACB=30°,∴∠BDC=90°,
∴∠BOC=∠ODC+∠ACE=120°,故答案为120°.
10. 答案 2.5
解析 ∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,点A在BC的垂直平分线上,
∴BC=AB=5,
∵DB=DC,∴点D在BC的垂直平分线上,
∴AD垂直平分BC,∴BE=BC=2.5.
三、解答题
11.证明 ∵BM=CN,BC=AC,∴CM=AN,
又∵AB=AC,∠BAN=∠ACM=60°,∴△AMC≌△BNA,∴∠AMC=∠BNA,
∵∠MAN+∠ANB+∠AQN=180°,∠MAN+∠AMC+∠ACB=180°,∴∠AQN=∠ACB,
∵∠BQM=∠AQN,∴∠BQM=∠ACB=60°.
12.解析 (1)设点M、N运动x秒后重合,
由题意得x×1+10=2x,解得x=10,
故M、N运动10秒后重合.
(2)设点M、N运动t秒后,可得到等边△AMN,如图1,
易知AM=t×1=t厘米,AN=AB-BN=(10-2t)厘米,
∵△ABC为等边三角形,∴∠A=60°,
∵△AMN是等边三角形,∴AM=AN,即t=10-2t,解得t=,
∴点M、N运动秒后,可得到等边△AMN.
(3)当点M、N在BC边上运动时,存在以MN为底边的等腰△AMN.
由(1)知10秒时M、N两点重合,恰好在C处,
如图2,假设△AMN是等腰三角形,且AN=AM,
∴∠AMN=∠ANM,∴∠AMC=∠ANB,
∵△ABC是等边三角形,∴∠C=∠B,AC=AB,
在△ACM和△ABN中,
∴△ACM≌△ABN(AAS),∴CM=BN,
设当点M、N运动的时间为y秒时,△AMN是等腰三角形,
∴CM=(y-10)厘米,NB=(30-2y)厘米,∴y-10=30-2y,解得y=,故假设成立.
∴当点M、N在BC边上运动时,存在以MN为底边的等腰△AMN,此时M、N运动的时间为秒.
13.解析 (1)∵DB=DE,∴∠E=∠DBE,
∵△ABC是等边三角形,BD是AC边上的高,
∴∠DBC=30°,∴∠E=∠DBE=30°,
∴∠BDE=180°-30°-30°=120°.
(2)证明:∵△ABC是等边三角形,∴∠ACB=60°,
∵∠E=30°,∴∠CDE=∠ACB-∠E=30°,
∴∠CDE=∠E,∴CD=CE,
∴△CED是等腰三角形.
14.解析 △APQ为等边三角形.
证明:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
