2022—2023学年人教版数学八年级上册 13.3.2 等边三角形第2课时 课堂提升训练试卷 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 13.3.2 等边三角形第2课时 课堂提升训练试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 304.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 18:55:07 | ||
图片预览


文档简介
2022-2023学年度人教版初中八年级数学课堂提升训练试卷
班级 姓名
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形第2课时
一、选择题
1. 已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“AB=AC”,那么△ABC是等边三角形;
②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A.3个 B.2个 C.1个 D.0个
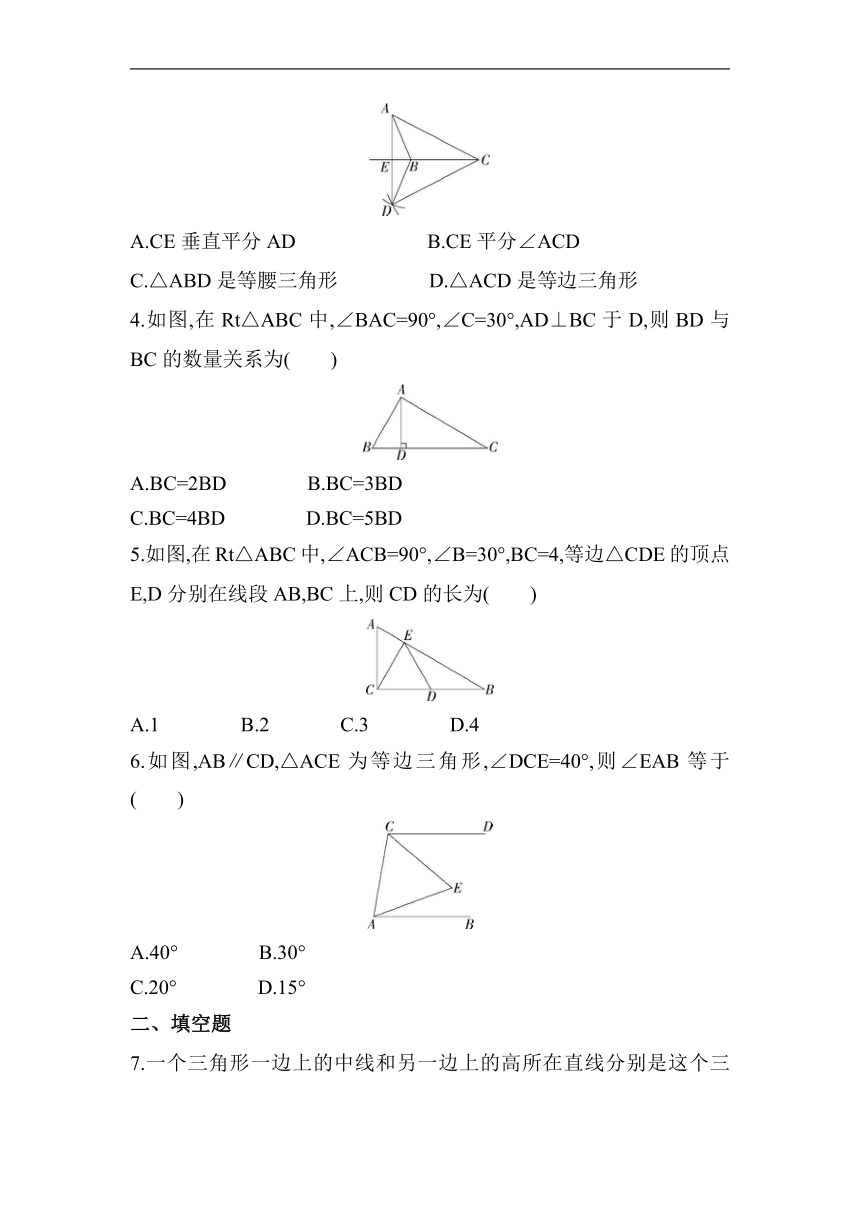
2.如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
3. 如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧,再以点C为圆心,AC长为半径画弧,两弧交于点D,连接AD,BD,CD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
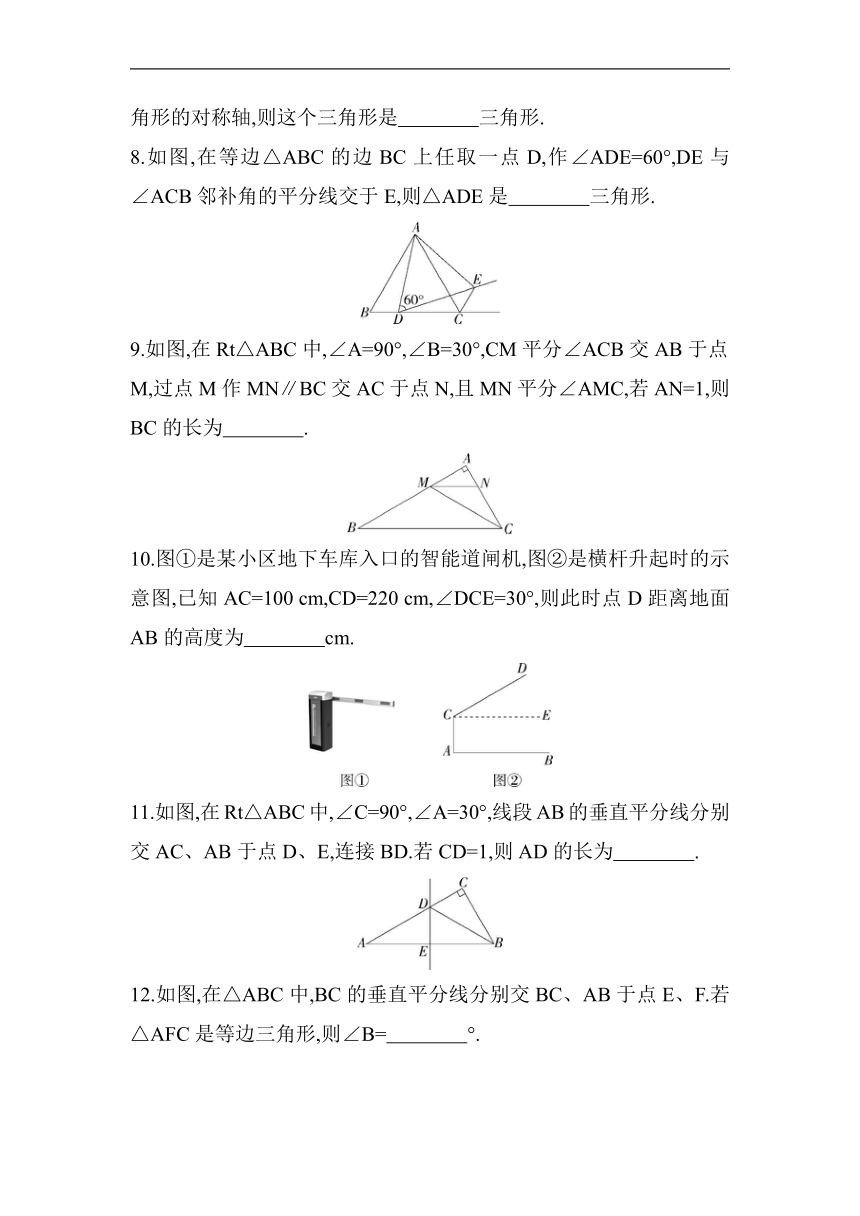
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,则BD与BC的数量关系为( )
A.BC=2BD B.BC=3BD
C.BC=4BD D.BC=5BD
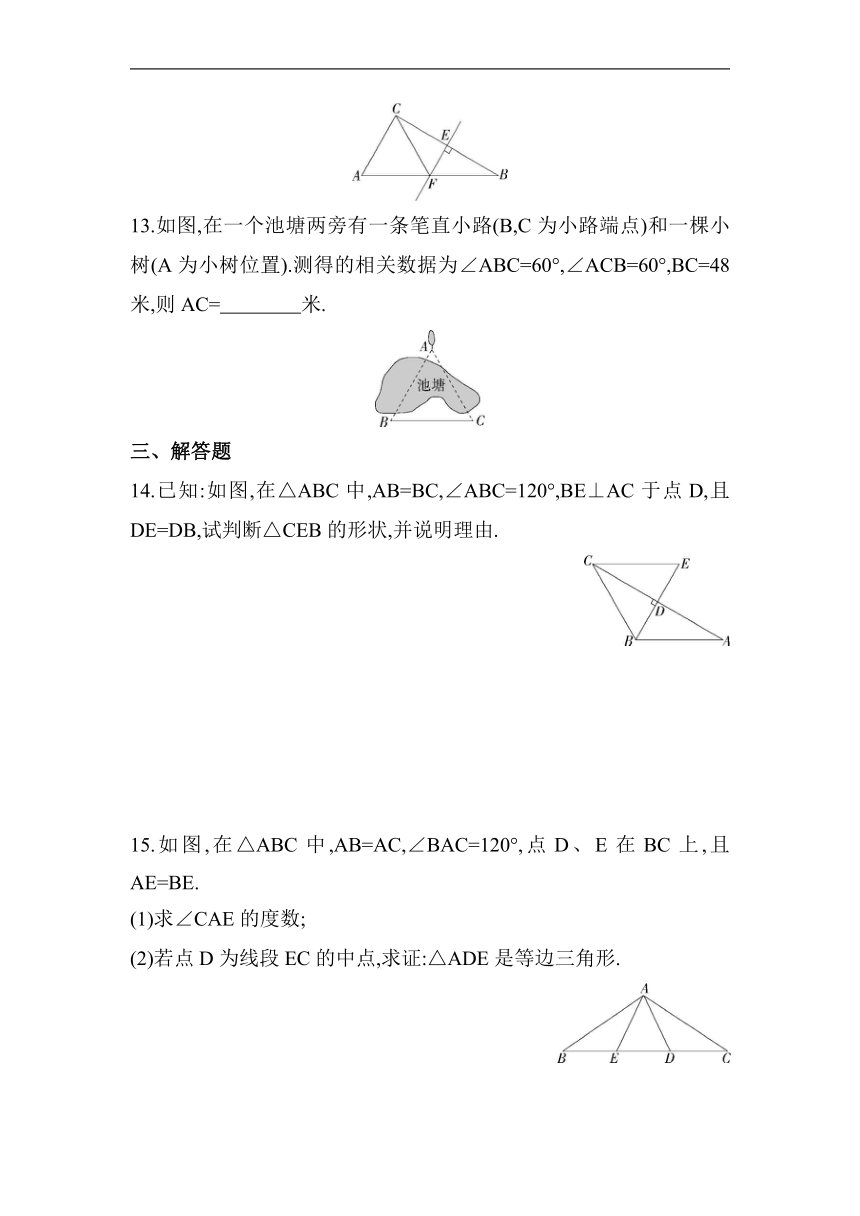
5.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4,等边△CDE的顶点E,D分别在线段AB,BC上,则CD的长为( )
A.1 B.2 C.3 D.4
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30°
C.20° D.15°
二、填空题
7.一个三角形一边上的中线和另一边上的高所在直线分别是这个三角形的对称轴,则这个三角形是 三角形.
8.如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE与∠ACB邻补角的平分线交于E,则△ADE是 三角形.
9.如图,在Rt△ABC中,∠A=90°,∠B=30°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为 .
10.图①是某小区地下车库入口的智能道闸机,图②是横杆升起时的示意图,已知AC=100 cm,CD=220 cm,∠DCE=30°,则此时点D距离地面AB的高度为 cm.
11.如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 .
12.如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC是等边三角形,则∠B= °.
13.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
三、解答题
14.已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
15.如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在BC上,且AE=BE.
(1)求∠CAE的度数;
(2)若点D为线段EC的中点,求证:△ADE是等边三角形.
16.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD的位置关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形 若存在,请写出来并证明;若不存在,请说明理由.
答案全解全析
一、选择题
1.答案 A ①若添加的条件为AB=AC,由∠A=60°,利用有一个角为60°的等腰三角形为等边三角形可得出△ABC为等边三角形;
②若添加的条件为∠B=∠C,∵∠A=60°,∴∠B=∠C=60°,∴∠A=∠B=∠C,
∴△ABC为等边三角形;
③若添加的条件为边AB、BC上的高相等,如图所示:
已知:∠BAC=60°,AE⊥BC,CD⊥AB,且AE=CD.
求证:△ABC为等边三角形.
证明:∵AE⊥BC,CD⊥AB,∴∠ADC=∠AEC=90°,
在Rt△ADC和Rt△CEA中,∴Rt△ADC≌Rt△CEA(HL),
∴∠ACE=∠BAC=60°,∴∠B=60°=∠BAC=∠ACB,
∴△ABC为等边三角形.
综上,正确的说法有3个.
2.答案 B ∵△ABC为等边三角形,∴AB=AC,∠BAC=60°.
∵∠1=∠2,BE=CD,∴△ABE≌△ACD,
∴AE=AD,∠CAD=∠BAE=60°,∴△ADE是等边三角形.
3.答案 D 由题意得CA=CD,BA=BD,
∴CB所在直线是AD的垂直平分线,
即CE垂直平分AD,故A选项结论正确;
∵CA=CD,∴∠CAD=∠CDA,∵CE⊥AD,∴∠CEA=∠CED=90°,
∴∠ACE=∠DCE,即CE平分∠ACD,故B选项结论正确;
∵DB=AB,∴△ABD是等腰三角形,故C选项结论正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项结论错误.
4. 答案 C ∵∠BAC=90°,∠C=30°,
∴∠B=180°-∠BAC-∠C=60°,BC=2AB,
∵AD⊥BC,∴∠ADB=90°,
∴∠BAD=180°-∠ADB-∠B=30°,∴AB=2BD,
∴BC=4BD.故选C.
5. 答案 B ∵△CDE为等边三角形,∴∠ECD=60°,CE=CD,
∵∠B=30°,∴∠CEB=180°-60°-30°=90°,
∴CE⊥AB,即△CBE为直角三角形,
∴CD=CE=BC=×4=2,故选B.
6. 答案 C ∵AB∥CD,∴∠DCA+∠CAB=180°,
即∠DCE+∠ECA+∠EAC+∠EAB=180°,
∵△ACE为等边三角形,
∴∠ECA=∠EAC=60°,
∴∠EAB=180°-40°-60°-60°=20°.故选C.
二、填空题
7.答案 等边
解析 如图所示,△ABC中,AD是边BC上的高,BE是边AC上的中线,
∵AD,BE所在直线分别是三角形ABC的对称轴,
∴△ABD≌△ACD,△BAE≌△BCE,
∴AB=AC,AB=BC,∴AB=AC=BC,
∴△ABC为等边三角形.
8.答案 等边
解析 如图,过D作AC的平行线交AB于P,
∵△ABC为等边三角形,∴∠BAC=∠ACB=∠B=60°,AB=BC,
∵AC∥PD,∴∠BPD=∠BDP=∠BAC=∠ACB=60°,
∴△BDP为等边三角形,∴BD=BP,∴AP=CD,
∵∠BPD为△ADP的外角,∴∠ADP+∠DAP=∠BPD=60°,
∵∠ADP+∠EDC=180°-∠BDP-∠ADE=60°,
∴∠ADP+∠DAP=∠ADP+∠EDC,∴∠DAP=∠EDC,
∵∠ACB=60°,∴∠ACF=120°,
∵CE平分∠ACF,∴∠ACE=60°,∴∠DCE=120°,
∵∠BPD=60°,∴∠APD=120°,∴∠APD=∠DCE,
在△ADP和△DEC中,
∴△ADP≌△DEC(ASA),∴AD=DE,
∵∠ADE=60°,∴△ADE是等边三角形.
9. 答案 6
解析 ∵∠A=90°,∠B=30°,∴∠ACB=60°,
∵MN∥BC,∴∠AMN=∠B=30°,
∵∠A=90°,AN=1,∴MN=2AN=2,
∵MN平分∠AMC,∴∠NMC=∠NMA=30°,
∵CM平分∠ACB,∴∠ACM=∠ACB=30°,
∴∠ACM=∠NMC,∴CN=MN=2,
∴AC=AN+CN=1+2=3,
∵在Rt△ABC中,∠A=90°,∠B=30°,
∴BC=2AC=2×3=6,故答案为6.
10. 答案 210
解析 如图所示,过D作DG⊥AB于G,交CE于点F,易知∠DFC=90°,FG=AC=100 cm,
∵∠DCE=30°,CD=220 cm,
∴DF=CD=×220=110(cm),
∴DG=DF+FG=110+100=210(cm).
11. 答案 2
解析 ∵DE垂直平分AB,
∴AD=BD,∴∠A=∠ABD,
∵∠A=30°,∴∠ABD=30°,
∴∠BDC=∠A+∠ABD=30°+30°=60°,
∵∠C=90°,∴∠CBD=30°,
∵CD=1,∴BD=2CD=2,∴AD=2.
12. 答案 30
解析 ∵EF垂直平分BC,
∴BF=CF,∴∠B=∠BCF,
∵△ACF为等边三角形,
∴∠AFC=60°,∴∠B=∠BCF=30°.
13. 答案 48
解析 ∵∠ABC=60°,∠ACB=60°,∴∠BAC=60°,
∴△ABC是等边三角形,∴AC=BC=48米.
三、解答题
14.解析 △CEB是等边三角形.
理由:∵AB=BC,∠ABC=120°,BE⊥AC,∴∠CBE=∠ABE=60°.
又∵DE=DB,BE⊥AC,∴CB=CE,∴△CEB是等边三角形.
15.解析 (1)∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵AE=BE,∴∠EAB=∠B=30°.
∵∠BAC=120°,∴∠CAE=∠BAC-∠EAB=120°-30°=90°.
(2)证明:由(1)知∠CAE=90°,
∵∠C=30°,∴∠AEC=60°,AE=CE,
∵点D为线段EC的中点,∴DE=CE=AE,
又∵∠AEC=60°,∴△ADE是等边三角形.
16.解析 (1)BE垂直平分AD.理由如下:
∵AM⊥BC,∴∠ABC+∠5=90°.
∵∠BAC=90°,∴∠ABC+∠C=90°,∴∠5=∠C.
∵AD平分∠MAC,∴∠3=∠4.
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∴∠BAD=∠ADB,
∴AB=DB,∴△BAD是等腰三角形.
又∵BE平分∠ABC,∴BF⊥AD,AF=DF,∴BE垂直平分AD.
(2)存在.△ABD、△AEG均是等边三角形.
证明:由(1)知BA=BD,
∵∠C=30°,∠BAC=90°,∴∠ABD=60°,∴△ABD是等边三角形.
∵BE平分∠ABC,∴∠2=∠ABC=30°,
∵AM⊥BC,∴∠BGM=∠AGE=60°.
又∵Rt△ACM中,∠C=30°,∴∠CAM=60°,
∴∠AEG=60°=∠AGE=∠GAE,∴△AEG是等边三角形.
班级 姓名
第十三章 轴对称
13.3 等腰三角形
13.3.2 等边三角形第2课时
一、选择题
1. 已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:
①如果添加条件“AB=AC”,那么△ABC是等边三角形;
②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;
③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.
上述说法中,正确的有( )
A.3个 B.2个 C.1个 D.0个
2.如图,E是等边△ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
3. 如图,在钝角三角形ABC中,∠ABC为钝角,以点B为圆心,AB长为半径画弧,再以点C为圆心,AC长为半径画弧,两弧交于点D,连接AD,BD,CD,CB的延长线交AD于点E.下列结论错误的是( )
A.CE垂直平分AD B.CE平分∠ACD
C.△ABD是等腰三角形 D.△ACD是等边三角形
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,则BD与BC的数量关系为( )
A.BC=2BD B.BC=3BD
C.BC=4BD D.BC=5BD
5.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4,等边△CDE的顶点E,D分别在线段AB,BC上,则CD的长为( )
A.1 B.2 C.3 D.4
6.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30°
C.20° D.15°
二、填空题
7.一个三角形一边上的中线和另一边上的高所在直线分别是这个三角形的对称轴,则这个三角形是 三角形.
8.如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE与∠ACB邻补角的平分线交于E,则△ADE是 三角形.
9.如图,在Rt△ABC中,∠A=90°,∠B=30°,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为 .
10.图①是某小区地下车库入口的智能道闸机,图②是横杆升起时的示意图,已知AC=100 cm,CD=220 cm,∠DCE=30°,则此时点D距离地面AB的高度为 cm.
11.如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 .
12.如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC是等边三角形,则∠B= °.
13.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
三、解答题
14.已知:如图,在△ABC中,AB=BC,∠ABC=120°,BE⊥AC于点D,且DE=DB,试判断△CEB的形状,并说明理由.
15.如图,在△ABC中,AB=AC,∠BAC=120°,点D、E在BC上,且AE=BE.
(1)求∠CAE的度数;
(2)若点D为线段EC的中点,求证:△ADE是等边三角形.
16.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.
(1)判断直线BE与线段AD的位置关系,并说明理由;
(2)若∠C=30°,图中是否存在等边三角形 若存在,请写出来并证明;若不存在,请说明理由.
答案全解全析
一、选择题
1.答案 A ①若添加的条件为AB=AC,由∠A=60°,利用有一个角为60°的等腰三角形为等边三角形可得出△ABC为等边三角形;
②若添加的条件为∠B=∠C,∵∠A=60°,∴∠B=∠C=60°,∴∠A=∠B=∠C,
∴△ABC为等边三角形;
③若添加的条件为边AB、BC上的高相等,如图所示:
已知:∠BAC=60°,AE⊥BC,CD⊥AB,且AE=CD.
求证:△ABC为等边三角形.
证明:∵AE⊥BC,CD⊥AB,∴∠ADC=∠AEC=90°,
在Rt△ADC和Rt△CEA中,∴Rt△ADC≌Rt△CEA(HL),
∴∠ACE=∠BAC=60°,∴∠B=60°=∠BAC=∠ACB,
∴△ABC为等边三角形.
综上,正确的说法有3个.
2.答案 B ∵△ABC为等边三角形,∴AB=AC,∠BAC=60°.
∵∠1=∠2,BE=CD,∴△ABE≌△ACD,
∴AE=AD,∠CAD=∠BAE=60°,∴△ADE是等边三角形.
3.答案 D 由题意得CA=CD,BA=BD,
∴CB所在直线是AD的垂直平分线,
即CE垂直平分AD,故A选项结论正确;
∵CA=CD,∴∠CAD=∠CDA,∵CE⊥AD,∴∠CEA=∠CED=90°,
∴∠ACE=∠DCE,即CE平分∠ACD,故B选项结论正确;
∵DB=AB,∴△ABD是等腰三角形,故C选项结论正确;
∵AD与AC不一定相等,
∴△ACD不一定是等边三角形,故D选项结论错误.
4. 答案 C ∵∠BAC=90°,∠C=30°,
∴∠B=180°-∠BAC-∠C=60°,BC=2AB,
∵AD⊥BC,∴∠ADB=90°,
∴∠BAD=180°-∠ADB-∠B=30°,∴AB=2BD,
∴BC=4BD.故选C.
5. 答案 B ∵△CDE为等边三角形,∴∠ECD=60°,CE=CD,
∵∠B=30°,∴∠CEB=180°-60°-30°=90°,
∴CE⊥AB,即△CBE为直角三角形,
∴CD=CE=BC=×4=2,故选B.
6. 答案 C ∵AB∥CD,∴∠DCA+∠CAB=180°,
即∠DCE+∠ECA+∠EAC+∠EAB=180°,
∵△ACE为等边三角形,
∴∠ECA=∠EAC=60°,
∴∠EAB=180°-40°-60°-60°=20°.故选C.
二、填空题
7.答案 等边
解析 如图所示,△ABC中,AD是边BC上的高,BE是边AC上的中线,
∵AD,BE所在直线分别是三角形ABC的对称轴,
∴△ABD≌△ACD,△BAE≌△BCE,
∴AB=AC,AB=BC,∴AB=AC=BC,
∴△ABC为等边三角形.
8.答案 等边
解析 如图,过D作AC的平行线交AB于P,
∵△ABC为等边三角形,∴∠BAC=∠ACB=∠B=60°,AB=BC,
∵AC∥PD,∴∠BPD=∠BDP=∠BAC=∠ACB=60°,
∴△BDP为等边三角形,∴BD=BP,∴AP=CD,
∵∠BPD为△ADP的外角,∴∠ADP+∠DAP=∠BPD=60°,
∵∠ADP+∠EDC=180°-∠BDP-∠ADE=60°,
∴∠ADP+∠DAP=∠ADP+∠EDC,∴∠DAP=∠EDC,
∵∠ACB=60°,∴∠ACF=120°,
∵CE平分∠ACF,∴∠ACE=60°,∴∠DCE=120°,
∵∠BPD=60°,∴∠APD=120°,∴∠APD=∠DCE,
在△ADP和△DEC中,
∴△ADP≌△DEC(ASA),∴AD=DE,
∵∠ADE=60°,∴△ADE是等边三角形.
9. 答案 6
解析 ∵∠A=90°,∠B=30°,∴∠ACB=60°,
∵MN∥BC,∴∠AMN=∠B=30°,
∵∠A=90°,AN=1,∴MN=2AN=2,
∵MN平分∠AMC,∴∠NMC=∠NMA=30°,
∵CM平分∠ACB,∴∠ACM=∠ACB=30°,
∴∠ACM=∠NMC,∴CN=MN=2,
∴AC=AN+CN=1+2=3,
∵在Rt△ABC中,∠A=90°,∠B=30°,
∴BC=2AC=2×3=6,故答案为6.
10. 答案 210
解析 如图所示,过D作DG⊥AB于G,交CE于点F,易知∠DFC=90°,FG=AC=100 cm,
∵∠DCE=30°,CD=220 cm,
∴DF=CD=×220=110(cm),
∴DG=DF+FG=110+100=210(cm).
11. 答案 2
解析 ∵DE垂直平分AB,
∴AD=BD,∴∠A=∠ABD,
∵∠A=30°,∴∠ABD=30°,
∴∠BDC=∠A+∠ABD=30°+30°=60°,
∵∠C=90°,∴∠CBD=30°,
∵CD=1,∴BD=2CD=2,∴AD=2.
12. 答案 30
解析 ∵EF垂直平分BC,
∴BF=CF,∴∠B=∠BCF,
∵△ACF为等边三角形,
∴∠AFC=60°,∴∠B=∠BCF=30°.
13. 答案 48
解析 ∵∠ABC=60°,∠ACB=60°,∴∠BAC=60°,
∴△ABC是等边三角形,∴AC=BC=48米.
三、解答题
14.解析 △CEB是等边三角形.
理由:∵AB=BC,∠ABC=120°,BE⊥AC,∴∠CBE=∠ABE=60°.
又∵DE=DB,BE⊥AC,∴CB=CE,∴△CEB是等边三角形.
15.解析 (1)∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵AE=BE,∴∠EAB=∠B=30°.
∵∠BAC=120°,∴∠CAE=∠BAC-∠EAB=120°-30°=90°.
(2)证明:由(1)知∠CAE=90°,
∵∠C=30°,∴∠AEC=60°,AE=CE,
∵点D为线段EC的中点,∴DE=CE=AE,
又∵∠AEC=60°,∴△ADE是等边三角形.
16.解析 (1)BE垂直平分AD.理由如下:
∵AM⊥BC,∴∠ABC+∠5=90°.
∵∠BAC=90°,∴∠ABC+∠C=90°,∴∠5=∠C.
∵AD平分∠MAC,∴∠3=∠4.
∵∠BAD=∠5+∠3,∠ADB=∠C+∠4,∴∠BAD=∠ADB,
∴AB=DB,∴△BAD是等腰三角形.
又∵BE平分∠ABC,∴BF⊥AD,AF=DF,∴BE垂直平分AD.
(2)存在.△ABD、△AEG均是等边三角形.
证明:由(1)知BA=BD,
∵∠C=30°,∠BAC=90°,∴∠ABD=60°,∴△ABD是等边三角形.
∵BE平分∠ABC,∴∠2=∠ABC=30°,
∵AM⊥BC,∴∠BGM=∠AGE=60°.
又∵Rt△ACM中,∠C=30°,∴∠CAM=60°,
∴∠AEG=60°=∠AGE=∠GAE,∴△AEG是等边三角形.
