人教版九年级上册22.1.3 二次函数y=a(x-h)2的图象和性质 (第2课时)课件 (共17张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.3 二次函数y=a(x-h)2的图象和性质 (第2课时)课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 244.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 21:08:05 | ||
图片预览




文档简介
(共17张PPT)
22.1.3 第2课时 二次函数y=a(x-h)2的图象和性质
第二十二章 二次函数
22.1.3 第2课时 二次函数y=a(x-h)2的图象和性质
知识回顾
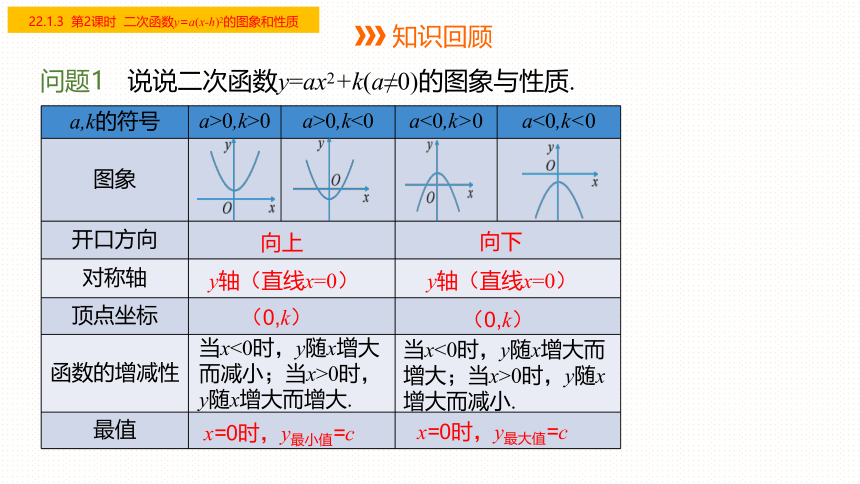
问题1 说说二次函数y=ax2+k(a≠0)的图象与性质.
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,k)
(0,k)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题2 二次函数y=ax2+k(a≠0)与y=ax2(a≠0)的图象有何关系?
二次函数y=ax2+k(a ≠ 0)的图象可以由y=ax2(a ≠ 0)
的图象平移得到:
当k > 0 时,向上平移k个单位长度得到.
当k < 0 时,向下平移-k个单位长度得到.
问题3 函数 的图象,能否也可以由函数 平移得到?
获取新知
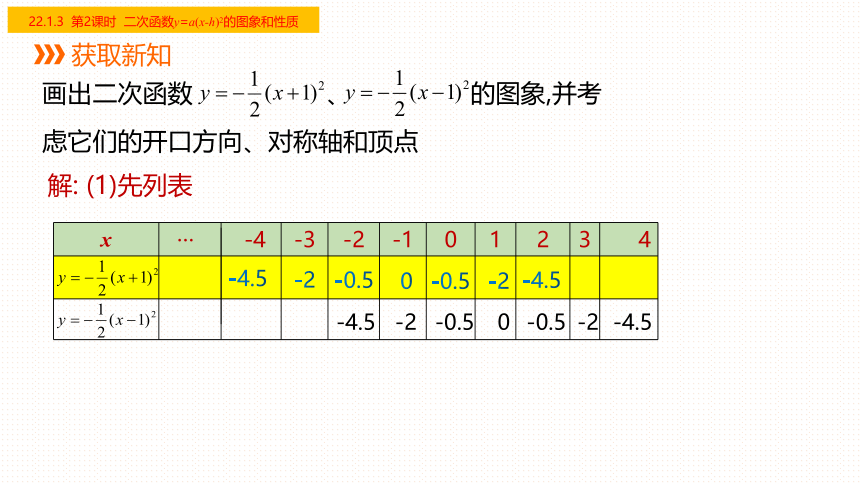
x -4 -3 -2 -1 0 1 2 3 4
解: (1)先列表
画出二次函数 、 的图象,并考虑它们的开口方向、对称轴和顶点
-2
…
0
-0.5
-2
-0.5
-4.5
-4.5
-2
-0.5
0
-4.5
-2
-0.5
-4.5
(2)描点
(3)连线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
y= x2
y= (x-1)2
y= (x+1)2
x -4 -3 -2 -1 0 1 2 3
-2
…
0
-0.5
-2
-0.5
-4.5
…
4
-4.5
-2
-0.5
0
-4.5
-2
-0.5
-4.5
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
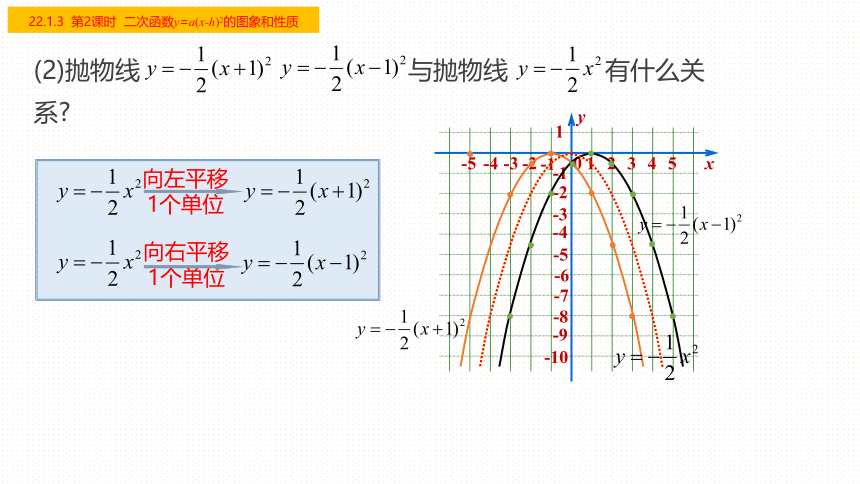
(1)抛物线 与 的开口方向、对称轴、顶点:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
向左平移1个单位
(2)抛物线 与抛物线 有什么关系
向右平移
1个单位
x
y
一般地,抛物线y=a(x-h)2有如下特点:
(1)对称轴是x=h;
(2)顶点是(h,0).
(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向右平移; h<0,向左平移
左右平移规律:括号内左加右减;括号外不变.
y=a(x-h)2 a>0 a<0
图象
开口
对称性
顶点
增减性
开口向上
开口向下
a的绝对值越大,开口越小
直线 x=h
顶点是最低点
顶点是最高点
在对称轴左侧(x在对称轴右侧(x>h)递增
在对称轴左侧(x在对称轴右侧(x>h)递减
h>0
h<0
h<0
h>0
(h,0)
二次函数 y=a(x-h)2(a ≠ 0)的性质
归纳总结
例题讲解
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,解得 ,
∴平移后二次函数关系式为y= (x-3)2.
例2 已知抛物线y=-(x+1)2上的两点A(x1,y1),B(x2,y2),如果x1<x2<-1,那么下列结论成立的是( )
A.y1<y2<0 B.0<y1<y2
C.0<y2<y1 D.y2<y1<0
A
随堂演练
1.抛物线y=-5(x-2)2的顶点坐标是( )
A.(-2,0) B.(2,0)
C.(0,-2) D.(0,2)
B
2. 在下列二次函数中,其图象的对称轴为直线x=-2的是( )
A.y=(x+2)2 B.y=2x2-2
C.y=-2x2-2 D.y=2(x-2)2
A
3. 把抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是( )
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向上平移2个单位长度
D.向下平移2个单位长度
A
4. 二次函数y=-3 (x-5)2的图象可有抛物线y=-3x2沿___轴向___平移___个单位得到,它的开口向___,顶点坐标是_______,对称轴是_________.当x=___时,y有最____值.当x___5时,y随x的增大而增大;当x___5时,y随x的增大而减小.
x
右
下
大
5
(5,0)
直线x=5
5
<
>
5.已知抛物线y=3(x+2)2.
(1)指出抛物线的开口方向;
(2)指出抛物线的顶点坐标;
(3)当x为何值时,y随x的增大而增大
解:(1) 抛物线开口向上.
(2)抛物线的顶点坐标为(-2,0).
(3)当x>-2时,y随x的增大而增大.
课堂小结
y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=h
a>0,开口向上
a<0,开口向下
y=ax2
(h,0)
性质
a>0,xx>h,y随x的增大而增大
a<0,xx>h,y随x的增大而减小
22.1.3 第2课时 二次函数y=a(x-h)2的图象和性质
第二十二章 二次函数
22.1.3 第2课时 二次函数y=a(x-h)2的图象和性质
知识回顾
问题1 说说二次函数y=ax2+k(a≠0)的图象与性质.
a,k的符号 a>0,k>0 a>0,k<0 a<0,k>0 a<0,k<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,k)
(0,k)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题2 二次函数y=ax2+k(a≠0)与y=ax2(a≠0)的图象有何关系?
二次函数y=ax2+k(a ≠ 0)的图象可以由y=ax2(a ≠ 0)
的图象平移得到:
当k > 0 时,向上平移k个单位长度得到.
当k < 0 时,向下平移-k个单位长度得到.
问题3 函数 的图象,能否也可以由函数 平移得到?
获取新知
x -4 -3 -2 -1 0 1 2 3 4
解: (1)先列表
画出二次函数 、 的图象,并考虑它们的开口方向、对称轴和顶点
-2
…
0
-0.5
-2
-0.5
-4.5
-4.5
-2
-0.5
0
-4.5
-2
-0.5
-4.5
(2)描点
(3)连线
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
y= x2
y= (x-1)2
y= (x+1)2
x -4 -3 -2 -1 0 1 2 3
-2
…
0
-0.5
-2
-0.5
-4.5
…
4
-4.5
-2
-0.5
0
-4.5
-2
-0.5
-4.5
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
(1)抛物线 与 的开口方向、对称轴、顶点:
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
0
-1
-2
-3
-4
-5
-10
向左平移1个单位
(2)抛物线 与抛物线 有什么关系
向右平移
1个单位
x
y
一般地,抛物线y=a(x-h)2有如下特点:
(1)对称轴是x=h;
(2)顶点是(h,0).
(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向右平移; h<0,向左平移
左右平移规律:括号内左加右减;括号外不变.
y=a(x-h)2 a>0 a<0
图象
开口
对称性
顶点
增减性
开口向上
开口向下
a的绝对值越大,开口越小
直线 x=h
顶点是最低点
顶点是最高点
在对称轴左侧(x
在对称轴左侧(x
h>0
h<0
h<0
h>0
(h,0)
二次函数 y=a(x-h)2(a ≠ 0)的性质
归纳总结
例题讲解
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,解得 ,
∴平移后二次函数关系式为y= (x-3)2.
例2 已知抛物线y=-(x+1)2上的两点A(x1,y1),B(x2,y2),如果x1<x2<-1,那么下列结论成立的是( )
A.y1<y2<0 B.0<y1<y2
C.0<y2<y1 D.y2<y1<0
A
随堂演练
1.抛物线y=-5(x-2)2的顶点坐标是( )
A.(-2,0) B.(2,0)
C.(0,-2) D.(0,2)
B
2. 在下列二次函数中,其图象的对称轴为直线x=-2的是( )
A.y=(x+2)2 B.y=2x2-2
C.y=-2x2-2 D.y=2(x-2)2
A
3. 把抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是( )
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向上平移2个单位长度
D.向下平移2个单位长度
A
4. 二次函数y=-3 (x-5)2的图象可有抛物线y=-3x2沿___轴向___平移___个单位得到,它的开口向___,顶点坐标是_______,对称轴是_________.当x=___时,y有最____值.当x___5时,y随x的增大而增大;当x___5时,y随x的增大而减小.
x
右
下
大
5
(5,0)
直线x=5
5
<
>
5.已知抛物线y=3(x+2)2.
(1)指出抛物线的开口方向;
(2)指出抛物线的顶点坐标;
(3)当x为何值时,y随x的增大而增大
解:(1) 抛物线开口向上.
(2)抛物线的顶点坐标为(-2,0).
(3)当x>-2时,y随x的增大而增大.
课堂小结
y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=h
a>0,开口向上
a<0,开口向下
y=ax2
(h,0)
性质
a>0,x
a<0,x
同课章节目录
