2022-2023学年鲁教版(五四学制)九年级数学上册 第1章反比例函数单元综合测试题(含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)九年级数学上册 第1章反比例函数单元综合测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 07:49:04 | ||
图片预览

文档简介
2022-2023学年鲁教版(五四学制)九年级数学上册《第1章反比例函数》
单元综合测试题(附答案)
一.选择题(共10小题,满分40分)
1.下列函数:①y=x﹣2,②y=,③y=x﹣1,④y=,y是x的反比例函数的个数有( )
A.0个 B.1个 C.2个 D.3个
2.已知y=(m+1)xm+2是反比例函数,则函数的图象在( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
3.函数y=﹣的大致图象是( )
A.B.C.D.
4.如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
A.平行四边形 B.菱形 C.矩形 D.任意四边形
5.对于反比例函数y=﹣,下列说法错误的是( )
A.图象分布在第二、四象限
B.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
C.图象经过点(1,﹣2)
D.当x>0时,y随x的增大而增大
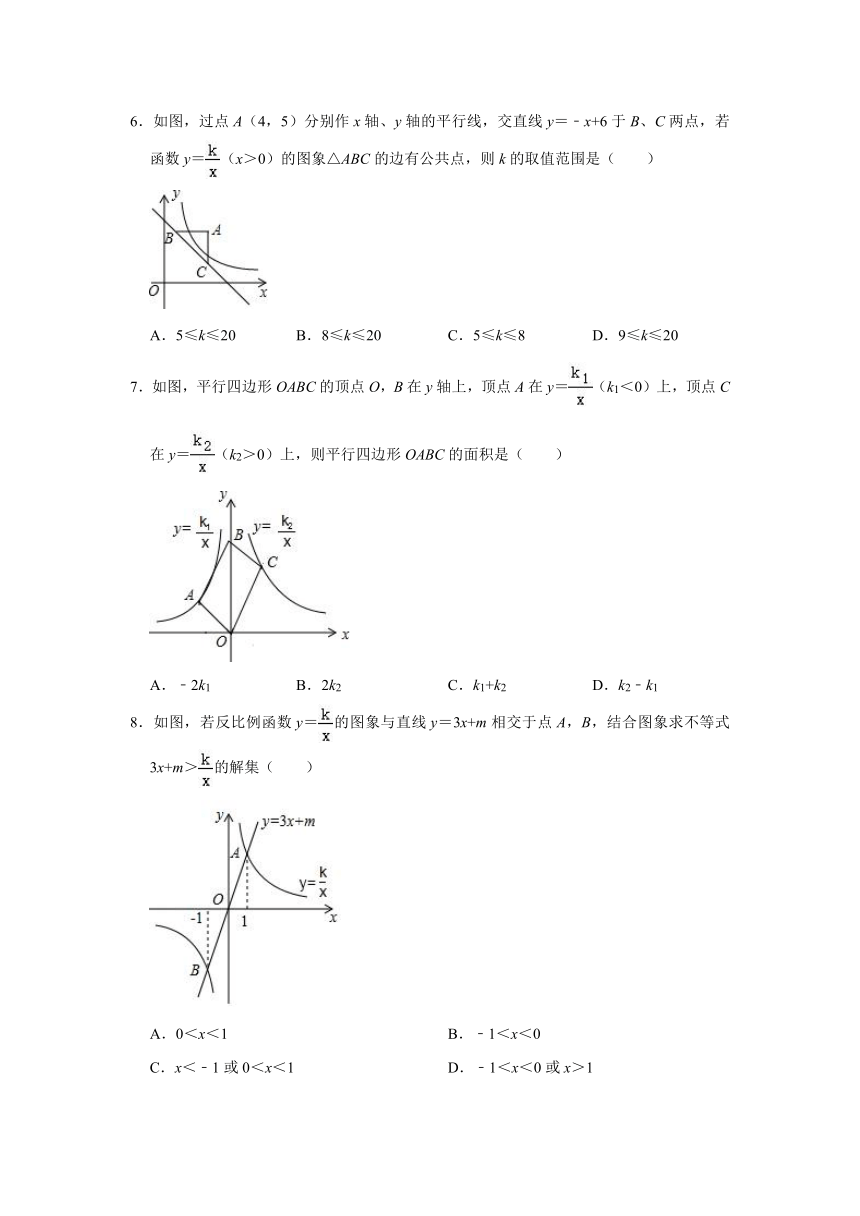
6.如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,若函数y=(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
A.5≤k≤20 B.8≤k≤20 C.5≤k≤8 D.9≤k≤20
7.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是( )
A.﹣2k1 B.2k2 C.k1+k2 D.k2﹣k1
8.如图,若反比例函数y=的图象与直线y=3x+m相交于点A,B,结合图象求不等式3x+m>的解集( )
A.0<x<1 B.﹣1<x<0
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
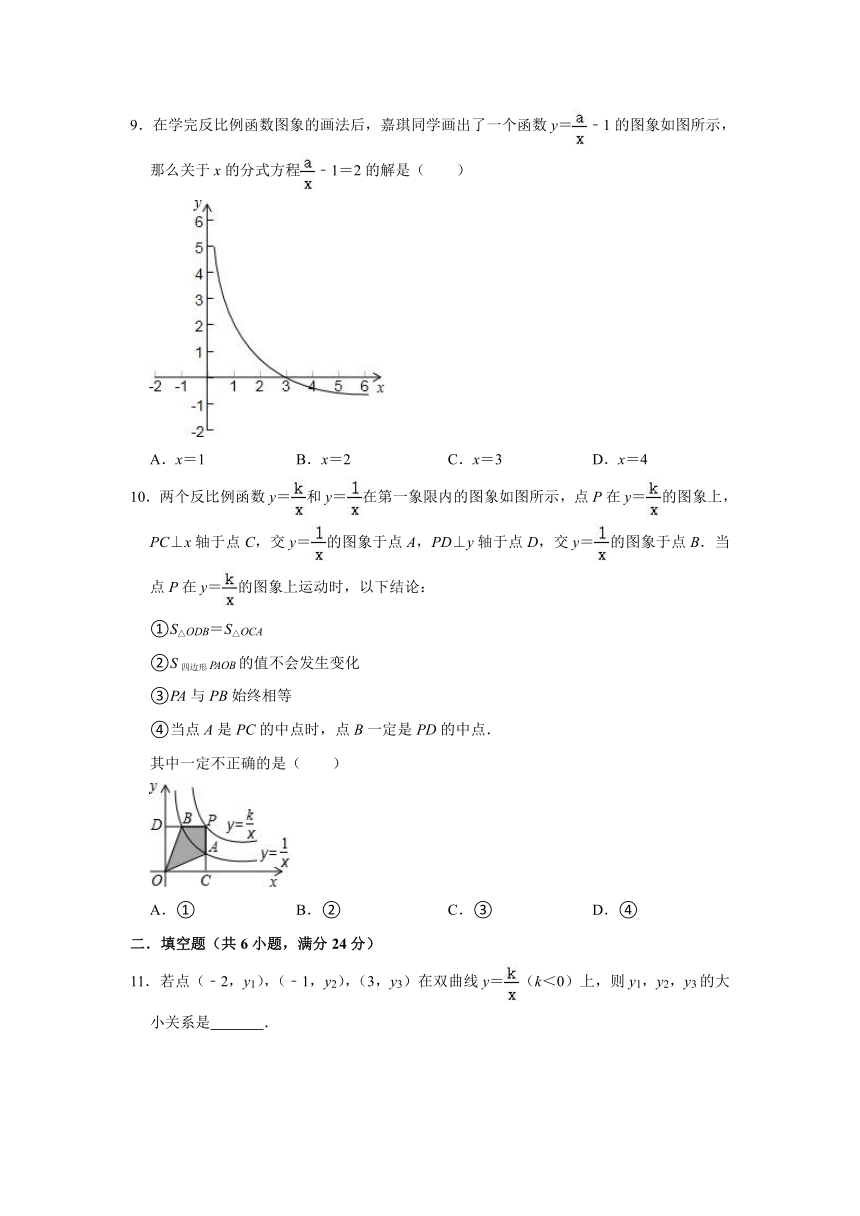
9.在学完反比例函数图象的画法后,嘉琪同学画出了一个函数y=﹣1的图象如图所示,那么关于x的分式方程﹣1=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
10.两个反比例函数y=和y=在第一象限内的图象如图所示,点P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B.当点P在y=的图象上运动时,以下结论:
①S△ODB=S△OCA
②S四边形PAOB的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )
A.① B.② C.③ D.④
二.填空题(共6小题,满分24分)
11.若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是 .
12.若m<﹣2,则下列函数:①y=(x>0);②y=﹣mx+1;③y=mx;④y=(m+1)x﹣1中y随x的增大而增大的函数是 .(填序号)
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
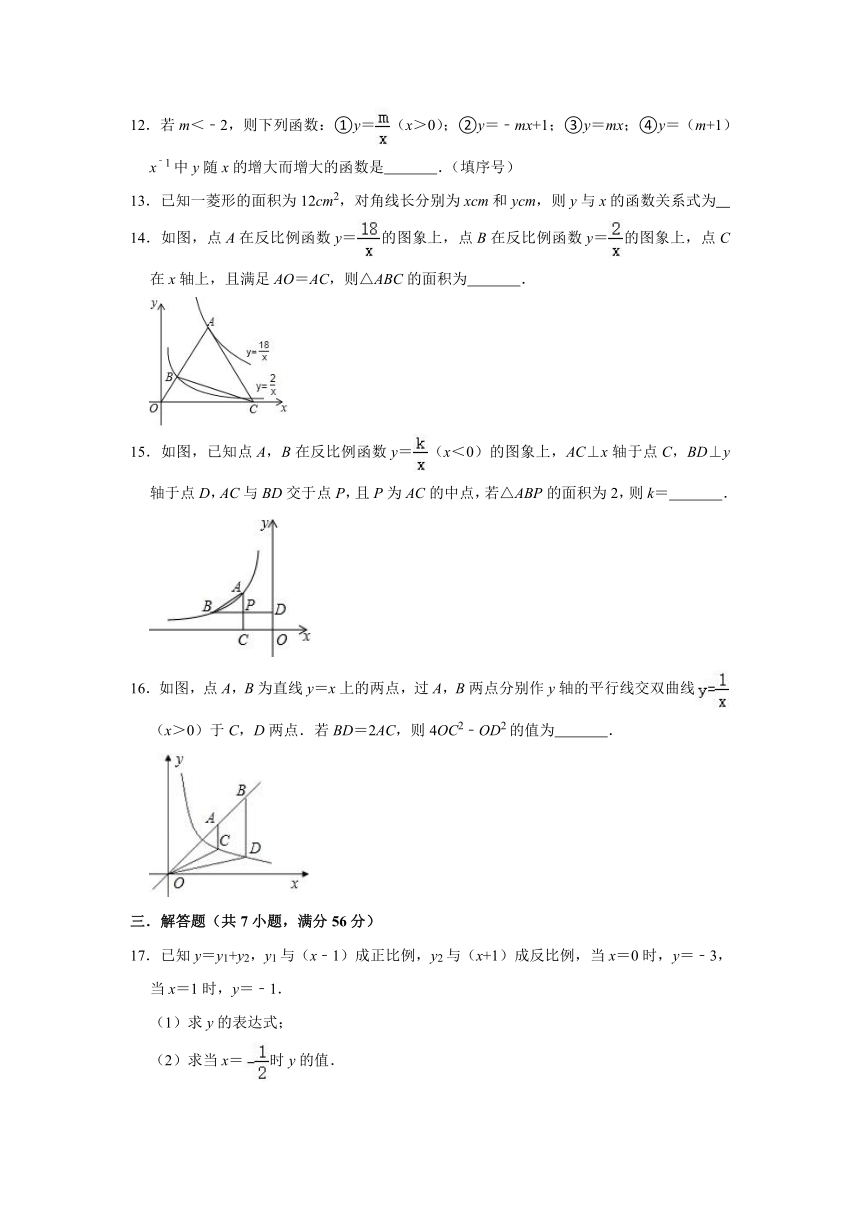
14.如图,点A在反比例函数y=的图象上,点B在反比例函数y=的图象上,点C在x轴上,且满足AO=AC,则△ABC的面积为 .
15.如图,已知点A,B在反比例函数y=(x<0)的图象上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,且P为AC的中点,若△ABP的面积为2,则k= .
16.如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线(x>0)于C,D两点.若BD=2AC,则4OC2﹣OD2的值为 .
三.解答题(共7小题,满分56分)
17.已知y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当x=0时,y=﹣3,当x=1时,y=﹣1.
(1)求y的表达式;
(2)求当x=时y的值.
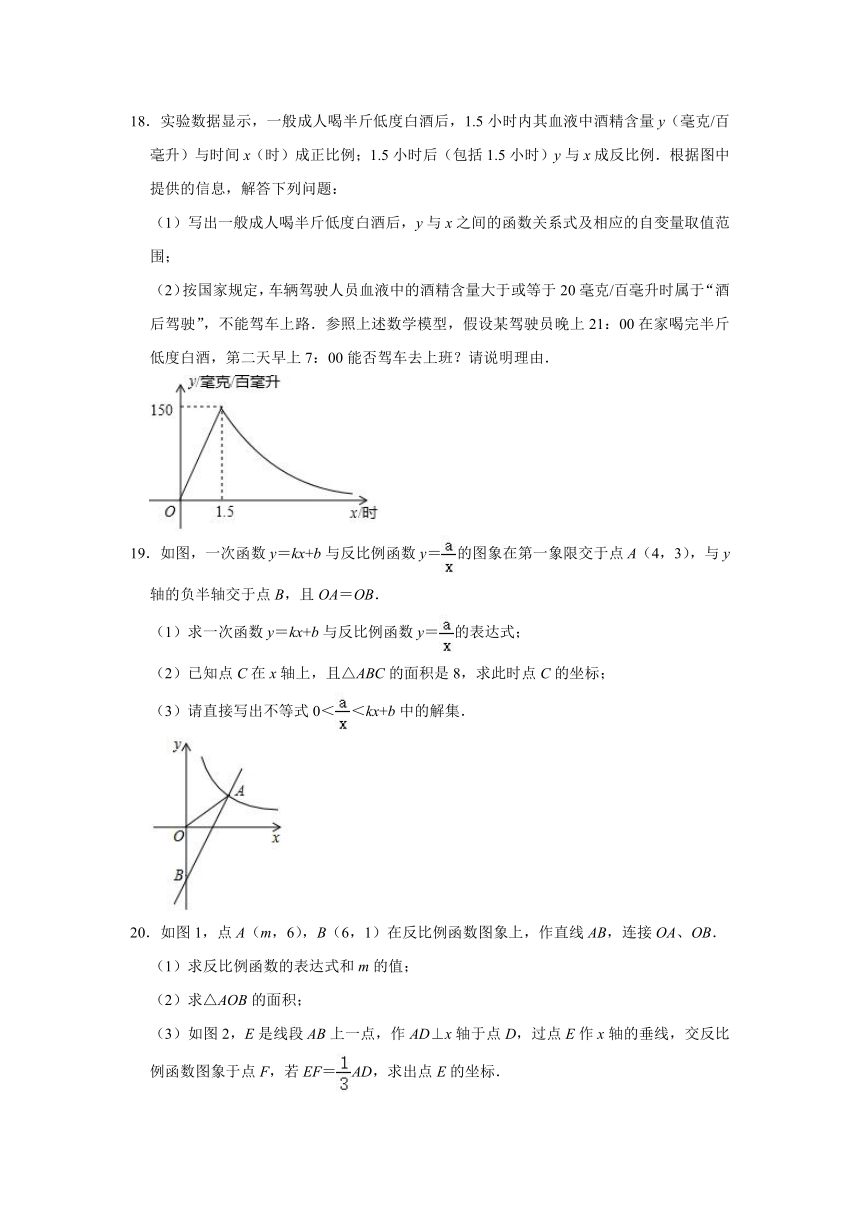
18.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)写出一般成人喝半斤低度白酒后,y与x之间的函数关系式及相应的自变量取值范围;
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上21:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
19.如图,一次函数y=kx+b与反比例函数y=的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b与反比例函数y=的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)请直接写出不等式0<<kx+b中的解集.
20.如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
21.已知,点A(1,3)和点B(3,m)在反比例函数的图象上:
(1)求m的值;
(2)点O是原点,求△AOB的面积;
(3)在平面直角坐标系xOy中,已知点M(0,﹣3),点N(a,﹣a+3),求MN+ON的最小值.
22.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(x>0,k>0)的图象上,点D的坐标为(4,3).
(1)求反比例函数的关系式;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=(x>0,k>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(3)在x轴上是否存在一点P,使|PA﹣PB|有最大值,若存在,请求出点P坐标;若不存在,请说明理由.
23.如图,平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=﹣在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若y轴上一点M的纵坐标是4,且AM=BM,求点A的坐标;
(3)在(2)的条件下,若点P在y轴上,点Q是平面直角坐标系中的一点,当以点A、M、P、Q为顶点的四边形是菱形时,请直接写出点Q的坐标.
参考答案
一.选择题(共10小题,满分40分)
1.解:①y=x﹣2,y是x的一次函数,故错误;
②y=,y是x的正比例函数,故错误;
③y=x﹣1,y是x的反比例函数,故正确;
④y=,y是x+1的反比例函数,故错误.
综上所述,正确的结论只有1个.
故选:B.
2.解:依题意有m+2=﹣1,
解得m=﹣3,
因而函数是y=,
故函数经过第二、四象限.
故选:B.
3.解:因为k=﹣2,y=﹣<0,所以它的两个分支分别位于第三、四象限.
故选:D.
4.解:由反比例函数的对称性,得
OA=OC,OB=OD,
ABCD是平行四边形,
故选:A.
5.解:A、反比例函数y=﹣中的﹣2<0,则该函数图象分布在第二、四象限,故本选项说法正确.
B、反比例函数y=﹣中的﹣2<0,则该函数图象在每一象限内y随x的增大而增大,若点A(x1,y1),B(x2,y2)在同一象限内,当x1<x2,则y1<y2,故本选项说法错误.
C、当x=1时,y=﹣=﹣2,即图象经过点(1,﹣2),故本选项说法正确.
D、反比例函数y=﹣中的﹣2<0,则该函数图象在每一象限内y随x的增大而增大,则当当x>0时,y随x的增大而增大,故本选项说法正确.
故选:B.
6.解:∵过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,
∴点B的纵坐标为5,点C的横坐标为4,
将y=5代入y=﹣x+6,得x=1;将x=4代入y=﹣x+6得,y=2,
∴点B的坐标为(1,5),点C的坐标为(4,2),
∵函数y=(x>0)的图象与△ABC的边有公共点,点A(4,5),点B(1,5),
∴1×5≤k≤4×5
即5≤k≤20,
故选:A.
7.解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
根据∠AEB=∠CD0=90°,∠ABE=∠COD,AB=CO可得:△ABE≌△COD(AAS),
∴△ABE与△COD的面积相等,
又∵点C在y=的图象上,
∴△ABE的面积=△COD的面积相等=|k2|,
同理可得:△AOE的面积=△CBD的面积相等=|k1|,
∴平行四边形OABC的面积=2(|k2|+|k1|)=|k2|+|k1|=k2﹣k1,
故选:D.
8.解:由图象可知,直线y=3x+m在反比例函数y=的图象上方时,﹣1<x<0或x>1,
不等式3x+m>的解集为:,﹣1<x<0或x>1.
故选:D.
9.解:如图所示,函数y=﹣1的图象经过点(3,0),则﹣1=0
解得a=3,
所以,由﹣1=2得到:﹣1=2
解得x=1.
故选:A.
10.解:①∵点A、B均在反比例函数y=的图象上,且BD⊥y轴,AC⊥x轴,
∴S△ODB=,S△OCA=,
∴S△ODB=S△OCA,结论①正确;
②∵点P在反比例函数y=的图象上,且PC⊥x轴,PD⊥y轴,
∴S矩形OCPD=k,
∴S四边形PAOB=S矩形OCPD﹣S△ODB﹣S△OCA=k﹣1,结论②正确;
③设点P的坐标为(m,),则点B的坐标(,),点A(m,),
∴PA=﹣=,PB=m﹣=,
∴PA与PB的关系无法确定,结论③错误;
④(方法一)设点P的坐标为(m,),则点B的坐标(,),点A(m,),
∵点A是PC的中点,
∴k=2,
∴P(m,),B(,),
∴点B是PD的中点,结论④正确;
(方法二)连接OP,如图所示,
∵点A是PC的中点,
∴S△OAC=S△OAP.
∵S△ODP=S△OCP=k,S△ODB=S△OCA,
∴S△ODP﹣S△ODB=S△OCP﹣S△OCA,
即S△OBP=S△OAP,
∴S△OBP=S△OAC=S△OBD,
∴点B一定是PD的中点,结论④正确.
故选:C.
二.填空题(共6小题,满分24分)
11.解:∵点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,
∴(﹣2,y1),(﹣1,y2)分布在第二象限,(3,y3)在第四象限,每个象限内,y随x的增大而增大,
∴y3<y1<y2.
故答案为y3<y1<y2.
12.解:①∵m<﹣2,
∴当x>0时,函数y=中y随x的增大而增大;
②∵m<﹣2,
∴﹣m>2,
∴函数y=﹣mx+1中y随x的增大而增大;
③∵m<﹣2,
∴函数y=mx中y随x的增大而减小;
④∵m<﹣2,
∴m+1<﹣1,
∴函数y=(m+1)x﹣1在第二、四象限内y随x的增大而增大.
综上所述:y随x的增大而增大的函数是①②.
故答案为:①②.
13.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
14.解:
设点A的坐标为(a,),点B的坐标为(b,)
∵点C是x轴上一点,且AO=AC
∴点C的坐标为(2a,0)
设直线OA的解析式为y=kx,则=ka,
∴k=,
∴直线OA的解析式为:y=x,
又∵点B在直线OA上,
∴= b,
∴=9,
∴=3(负值不合题意,舍去)
∴S△ABC=S△AOC﹣S△OBC= 2a ﹣ 2a =18﹣6=12
故答案为:12
15.解:∵△ABP的面积为 BP AP=2,
∴BP AP=4,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A,B在反比例函数y=(x<0)的图象上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴|k|=OC AC=BP 2AP=8.
故答案为:﹣8.
16.解:设A(a,a),B(b,b),则C(a,),D(b,)
AC=a﹣,BD=b﹣,
∵BD=2AC,
∴b﹣=2(a﹣)
4OC2﹣OD2=4(a2+)﹣(b2+)
=4[+2]﹣[+2]=4+8﹣4﹣2=6.
故答案为:6.
三.解答题(共7小题,满分56分)
17.解:(1)∵y1与(x﹣1)成正比例,y2与(x+1)成反比例,
∴y1=k1(x﹣1),y2=,
∵y=y1+y2,当x=0时,y=﹣3,当x=1时,y=﹣1.
∴,
∴k2=﹣2,k1=1,
∴y=x﹣1﹣;
(2)当x=﹣,y=x﹣1﹣=﹣﹣1﹣=﹣.
18.解:(1)由题意可得:当0≤x≤1.5时,设函数关系式为:y=kx,
则150=1.5k,
解得:k=100,
故y=100x,
当1.5≤x时,设函数关系式为:y=,
则a=150×1.5=225,
解得:a=225,
故y=(x≥1.5),
综上所述:y与x之间的两个函数关系式为:y=;
(2)第二天早上7:00不能驾车去上班.
理由:∵晚上21:00到第二天早上7:00,有10小时,
∴x=10时,y==22.5>20,
∴第二天早上7:00不能驾车去上班.
19.解:(1)∵点A(4,3)在反比例函数y=的图象上,
∴a=4×3=12,
∴反比例函数解析式为y=;
∵OA=,OA=OB,点B在y轴负半轴上,
∴点B(0,﹣5).
把点A(4,3)、B(0,﹣5)代入y=kx+b中,
得,解得:,
∴一次函数的解析式为y=2x﹣5;
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,如图1所示.
令y=2x﹣5中y=0,则x=,
∴D(,0),
∴S△ABC=CD (yA﹣yB)=|m﹣||×[3﹣(﹣5)]=8,
解得:m=或m=.
故当△ABC的面积是8时,点C的坐标为(,0)或(,0);
(3)观察图象,由点A的坐标可知,不等式0<<kx+b中的解集为x>4.
20.解:(1)设反比例函数的解析式为y=,
将B(6,1)的坐标代入y=,得k=6.
∴反比例函数的解析式为y=.
将A(m,6)的坐标代入y=,得m=1.
(2)如图1,设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入上式,得
,解得:,
故直线AB的解析式为:y=﹣x+7,
∴M(0,7),N(7,0),
∴S△AOB=S△MON﹣S△AOM﹣S△BON=OM×ON﹣OM×|xA|﹣ON×|yB|
=×7×7﹣×7×1﹣×7×1=.
(3)设E点的坐标为(m,﹣m+7),则F(m,),
∴EF=﹣m+7﹣.
∵EF=AD,
∴﹣m+7﹣=×6.
解得m1=2,m2=3,
经检验,m1=2,m2=3是分式方程的根,
∴E的坐标为(2,5)或(3,4).
21.解:(1)∵点A,和点B在反比例函数y=的图象上
∴,解得 ,
∴m=1.
(2)过点 A,作AC⊥y轴于点C,过点 B作BD⊥x轴于点D,延长CA、DB交于点E得正方形CODE.如图1
S△AOB=S正方形CODE﹣S△AOC﹣S△BOD﹣S△ABE,
=OC×OD﹣AE BE,
=3×3﹣×2×2,
=4.
(3)如图2,由已知可得点N在直线y=﹣x+3上,
∵点A,(1,3)、B(3,1),
∴点C(0,3)、D(3,0),
∴直线y=﹣x+3过C、D两点,
∵点O与点E关于直线AC对称,
∴ON=EN,
∴ON+MN=EN+MN≥ME,
当点M、N、E三点共线时,ON+MN=ME此时,ON+MN的值最小.
∵ME=.
∴ON+MN的最小值是3.
22.解:(1)如图1,延长AD交x轴于点F,
∵四边形ABCD是菱形,
∴AD=OD,AD∥OB,
∴AD⊥x轴,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴AF=DF+AD=DF+OD=8
∴A点坐标为:(4,8),
∵点A在反比例函数y=(x>0,k>0)的图象上,
∴k=4×8=32,
∴反比例函数的关系式为y=,
(2)∵将菱形ABCD向右平移,当点D落在反比例函数y=(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=,
x=,
∴OF′=,
∴FF′=﹣4=,
∴菱形ABCD平移的距离为:;
(3)如图2,∵点P在x轴上,当点A,B,P不在同一条直线上时,点A,B,P构成三角形,
∴|PA﹣PB|<AB,
∴当点A,B,P在同一条直线上时,|PA﹣PB|最大,
由(1)知,A(4,8),
由菱形的性质得到B(0,5),
设直线AB的方程为:y=ax+b(a≠0),则
,
解得,
故直线AB的方程为:y=x+5,
令y=0,则0=x+5,
∴x=﹣,
∴P(﹣,0).
23.解:(1)∵一次函数y=﹣x+b的图象交x轴于B,交y轴于C,则B(b,0),C(0,b),
∴OB=OC=﹣b,
∵∠BOC=90°
∴△OBC是等腰直角三角形,
∴∠BCO=45°.
(2)如图1中,作MN⊥AB于N.
∵M(0,4),MN⊥AC,直线AC的解析式为y=﹣x+b,
∴直线MN的解析式为y=x+4,
由,解得,
∴N(,),
∵MA=MB,MN⊥AB,
∴NA=BN,设A(m,n),
则有,解得,
∴A(﹣4,b+4),
∵点A在y=﹣上,
∴﹣4(b+4)=﹣4,
∴b=﹣3,
∴A(﹣4,1).
(3)如图2中,
由(2)可知A(﹣4,1),M(0,4),
∴AM==5,
当菱形以AM为边时,AQ=AQ′=5,AQ∥OM,可得Q(﹣4,﹣4),Q′(﹣4,6),
当A,Q关于y轴对称时,也满足条件,此时Q(4,1)
当AM为菱形的对角线时,设P″(0,b),
则有(4﹣b)2=42+(b﹣1)2,
∴b=﹣.
∴AQ″=MP″=,
∴Q″(﹣4,),
综上所述,满足条件的点Q坐标为(﹣4,﹣4)或(﹣4,6)或(﹣4,)或(4,1).
单元综合测试题(附答案)
一.选择题(共10小题,满分40分)
1.下列函数:①y=x﹣2,②y=,③y=x﹣1,④y=,y是x的反比例函数的个数有( )
A.0个 B.1个 C.2个 D.3个
2.已知y=(m+1)xm+2是反比例函数,则函数的图象在( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
3.函数y=﹣的大致图象是( )
A.B.C.D.
4.如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
A.平行四边形 B.菱形 C.矩形 D.任意四边形
5.对于反比例函数y=﹣,下列说法错误的是( )
A.图象分布在第二、四象限
B.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
C.图象经过点(1,﹣2)
D.当x>0时,y随x的增大而增大
6.如图,过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,若函数y=(x>0)的图象△ABC的边有公共点,则k的取值范围是( )
A.5≤k≤20 B.8≤k≤20 C.5≤k≤8 D.9≤k≤20
7.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是( )
A.﹣2k1 B.2k2 C.k1+k2 D.k2﹣k1
8.如图,若反比例函数y=的图象与直线y=3x+m相交于点A,B,结合图象求不等式3x+m>的解集( )
A.0<x<1 B.﹣1<x<0
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
9.在学完反比例函数图象的画法后,嘉琪同学画出了一个函数y=﹣1的图象如图所示,那么关于x的分式方程﹣1=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
10.两个反比例函数y=和y=在第一象限内的图象如图所示,点P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B.当点P在y=的图象上运动时,以下结论:
①S△ODB=S△OCA
②S四边形PAOB的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )
A.① B.② C.③ D.④
二.填空题(共6小题,满分24分)
11.若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是 .
12.若m<﹣2,则下列函数:①y=(x>0);②y=﹣mx+1;③y=mx;④y=(m+1)x﹣1中y随x的增大而增大的函数是 .(填序号)
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
14.如图,点A在反比例函数y=的图象上,点B在反比例函数y=的图象上,点C在x轴上,且满足AO=AC,则△ABC的面积为 .
15.如图,已知点A,B在反比例函数y=(x<0)的图象上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,且P为AC的中点,若△ABP的面积为2,则k= .
16.如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线(x>0)于C,D两点.若BD=2AC,则4OC2﹣OD2的值为 .
三.解答题(共7小题,满分56分)
17.已知y=y1+y2,y1与(x﹣1)成正比例,y2与(x+1)成反比例,当x=0时,y=﹣3,当x=1时,y=﹣1.
(1)求y的表达式;
(2)求当x=时y的值.
18.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)写出一般成人喝半斤低度白酒后,y与x之间的函数关系式及相应的自变量取值范围;
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上21:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
19.如图,一次函数y=kx+b与反比例函数y=的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b与反比例函数y=的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)请直接写出不等式0<<kx+b中的解集.
20.如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
21.已知,点A(1,3)和点B(3,m)在反比例函数的图象上:
(1)求m的值;
(2)点O是原点,求△AOB的面积;
(3)在平面直角坐标系xOy中,已知点M(0,﹣3),点N(a,﹣a+3),求MN+ON的最小值.
22.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(x>0,k>0)的图象上,点D的坐标为(4,3).
(1)求反比例函数的关系式;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=(x>0,k>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(3)在x轴上是否存在一点P,使|PA﹣PB|有最大值,若存在,请求出点P坐标;若不存在,请说明理由.
23.如图,平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=﹣在第二象限内的图象相交于点A,与x轴的负半轴交于点B,与y轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若y轴上一点M的纵坐标是4,且AM=BM,求点A的坐标;
(3)在(2)的条件下,若点P在y轴上,点Q是平面直角坐标系中的一点,当以点A、M、P、Q为顶点的四边形是菱形时,请直接写出点Q的坐标.
参考答案
一.选择题(共10小题,满分40分)
1.解:①y=x﹣2,y是x的一次函数,故错误;
②y=,y是x的正比例函数,故错误;
③y=x﹣1,y是x的反比例函数,故正确;
④y=,y是x+1的反比例函数,故错误.
综上所述,正确的结论只有1个.
故选:B.
2.解:依题意有m+2=﹣1,
解得m=﹣3,
因而函数是y=,
故函数经过第二、四象限.
故选:B.
3.解:因为k=﹣2,y=﹣<0,所以它的两个分支分别位于第三、四象限.
故选:D.
4.解:由反比例函数的对称性,得
OA=OC,OB=OD,
ABCD是平行四边形,
故选:A.
5.解:A、反比例函数y=﹣中的﹣2<0,则该函数图象分布在第二、四象限,故本选项说法正确.
B、反比例函数y=﹣中的﹣2<0,则该函数图象在每一象限内y随x的增大而增大,若点A(x1,y1),B(x2,y2)在同一象限内,当x1<x2,则y1<y2,故本选项说法错误.
C、当x=1时,y=﹣=﹣2,即图象经过点(1,﹣2),故本选项说法正确.
D、反比例函数y=﹣中的﹣2<0,则该函数图象在每一象限内y随x的增大而增大,则当当x>0时,y随x的增大而增大,故本选项说法正确.
故选:B.
6.解:∵过点A(4,5)分别作x轴、y轴的平行线,交直线y=﹣x+6于B、C两点,
∴点B的纵坐标为5,点C的横坐标为4,
将y=5代入y=﹣x+6,得x=1;将x=4代入y=﹣x+6得,y=2,
∴点B的坐标为(1,5),点C的坐标为(4,2),
∵函数y=(x>0)的图象与△ABC的边有公共点,点A(4,5),点B(1,5),
∴1×5≤k≤4×5
即5≤k≤20,
故选:A.
7.解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
根据∠AEB=∠CD0=90°,∠ABE=∠COD,AB=CO可得:△ABE≌△COD(AAS),
∴△ABE与△COD的面积相等,
又∵点C在y=的图象上,
∴△ABE的面积=△COD的面积相等=|k2|,
同理可得:△AOE的面积=△CBD的面积相等=|k1|,
∴平行四边形OABC的面积=2(|k2|+|k1|)=|k2|+|k1|=k2﹣k1,
故选:D.
8.解:由图象可知,直线y=3x+m在反比例函数y=的图象上方时,﹣1<x<0或x>1,
不等式3x+m>的解集为:,﹣1<x<0或x>1.
故选:D.
9.解:如图所示,函数y=﹣1的图象经过点(3,0),则﹣1=0
解得a=3,
所以,由﹣1=2得到:﹣1=2
解得x=1.
故选:A.
10.解:①∵点A、B均在反比例函数y=的图象上,且BD⊥y轴,AC⊥x轴,
∴S△ODB=,S△OCA=,
∴S△ODB=S△OCA,结论①正确;
②∵点P在反比例函数y=的图象上,且PC⊥x轴,PD⊥y轴,
∴S矩形OCPD=k,
∴S四边形PAOB=S矩形OCPD﹣S△ODB﹣S△OCA=k﹣1,结论②正确;
③设点P的坐标为(m,),则点B的坐标(,),点A(m,),
∴PA=﹣=,PB=m﹣=,
∴PA与PB的关系无法确定,结论③错误;
④(方法一)设点P的坐标为(m,),则点B的坐标(,),点A(m,),
∵点A是PC的中点,
∴k=2,
∴P(m,),B(,),
∴点B是PD的中点,结论④正确;
(方法二)连接OP,如图所示,
∵点A是PC的中点,
∴S△OAC=S△OAP.
∵S△ODP=S△OCP=k,S△ODB=S△OCA,
∴S△ODP﹣S△ODB=S△OCP﹣S△OCA,
即S△OBP=S△OAP,
∴S△OBP=S△OAC=S△OBD,
∴点B一定是PD的中点,结论④正确.
故选:C.
二.填空题(共6小题,满分24分)
11.解:∵点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y=(k<0)上,
∴(﹣2,y1),(﹣1,y2)分布在第二象限,(3,y3)在第四象限,每个象限内,y随x的增大而增大,
∴y3<y1<y2.
故答案为y3<y1<y2.
12.解:①∵m<﹣2,
∴当x>0时,函数y=中y随x的增大而增大;
②∵m<﹣2,
∴﹣m>2,
∴函数y=﹣mx+1中y随x的增大而增大;
③∵m<﹣2,
∴函数y=mx中y随x的增大而减小;
④∵m<﹣2,
∴m+1<﹣1,
∴函数y=(m+1)x﹣1在第二、四象限内y随x的增大而增大.
综上所述:y随x的增大而增大的函数是①②.
故答案为:①②.
13.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
14.解:
设点A的坐标为(a,),点B的坐标为(b,)
∵点C是x轴上一点,且AO=AC
∴点C的坐标为(2a,0)
设直线OA的解析式为y=kx,则=ka,
∴k=,
∴直线OA的解析式为:y=x,
又∵点B在直线OA上,
∴= b,
∴=9,
∴=3(负值不合题意,舍去)
∴S△ABC=S△AOC﹣S△OBC= 2a ﹣ 2a =18﹣6=12
故答案为:12
15.解:∵△ABP的面积为 BP AP=2,
∴BP AP=4,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A,B在反比例函数y=(x<0)的图象上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴|k|=OC AC=BP 2AP=8.
故答案为:﹣8.
16.解:设A(a,a),B(b,b),则C(a,),D(b,)
AC=a﹣,BD=b﹣,
∵BD=2AC,
∴b﹣=2(a﹣)
4OC2﹣OD2=4(a2+)﹣(b2+)
=4[+2]﹣[+2]=4+8﹣4﹣2=6.
故答案为:6.
三.解答题(共7小题,满分56分)
17.解:(1)∵y1与(x﹣1)成正比例,y2与(x+1)成反比例,
∴y1=k1(x﹣1),y2=,
∵y=y1+y2,当x=0时,y=﹣3,当x=1时,y=﹣1.
∴,
∴k2=﹣2,k1=1,
∴y=x﹣1﹣;
(2)当x=﹣,y=x﹣1﹣=﹣﹣1﹣=﹣.
18.解:(1)由题意可得:当0≤x≤1.5时,设函数关系式为:y=kx,
则150=1.5k,
解得:k=100,
故y=100x,
当1.5≤x时,设函数关系式为:y=,
则a=150×1.5=225,
解得:a=225,
故y=(x≥1.5),
综上所述:y与x之间的两个函数关系式为:y=;
(2)第二天早上7:00不能驾车去上班.
理由:∵晚上21:00到第二天早上7:00,有10小时,
∴x=10时,y==22.5>20,
∴第二天早上7:00不能驾车去上班.
19.解:(1)∵点A(4,3)在反比例函数y=的图象上,
∴a=4×3=12,
∴反比例函数解析式为y=;
∵OA=,OA=OB,点B在y轴负半轴上,
∴点B(0,﹣5).
把点A(4,3)、B(0,﹣5)代入y=kx+b中,
得,解得:,
∴一次函数的解析式为y=2x﹣5;
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,如图1所示.
令y=2x﹣5中y=0,则x=,
∴D(,0),
∴S△ABC=CD (yA﹣yB)=|m﹣||×[3﹣(﹣5)]=8,
解得:m=或m=.
故当△ABC的面积是8时,点C的坐标为(,0)或(,0);
(3)观察图象,由点A的坐标可知,不等式0<<kx+b中的解集为x>4.
20.解:(1)设反比例函数的解析式为y=,
将B(6,1)的坐标代入y=,得k=6.
∴反比例函数的解析式为y=.
将A(m,6)的坐标代入y=,得m=1.
(2)如图1,设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入上式,得
,解得:,
故直线AB的解析式为:y=﹣x+7,
∴M(0,7),N(7,0),
∴S△AOB=S△MON﹣S△AOM﹣S△BON=OM×ON﹣OM×|xA|﹣ON×|yB|
=×7×7﹣×7×1﹣×7×1=.
(3)设E点的坐标为(m,﹣m+7),则F(m,),
∴EF=﹣m+7﹣.
∵EF=AD,
∴﹣m+7﹣=×6.
解得m1=2,m2=3,
经检验,m1=2,m2=3是分式方程的根,
∴E的坐标为(2,5)或(3,4).
21.解:(1)∵点A,和点B在反比例函数y=的图象上
∴,解得 ,
∴m=1.
(2)过点 A,作AC⊥y轴于点C,过点 B作BD⊥x轴于点D,延长CA、DB交于点E得正方形CODE.如图1
S△AOB=S正方形CODE﹣S△AOC﹣S△BOD﹣S△ABE,
=OC×OD﹣AE BE,
=3×3﹣×2×2,
=4.
(3)如图2,由已知可得点N在直线y=﹣x+3上,
∵点A,(1,3)、B(3,1),
∴点C(0,3)、D(3,0),
∴直线y=﹣x+3过C、D两点,
∵点O与点E关于直线AC对称,
∴ON=EN,
∴ON+MN=EN+MN≥ME,
当点M、N、E三点共线时,ON+MN=ME此时,ON+MN的值最小.
∵ME=.
∴ON+MN的最小值是3.
22.解:(1)如图1,延长AD交x轴于点F,
∵四边形ABCD是菱形,
∴AD=OD,AD∥OB,
∴AD⊥x轴,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴AF=DF+AD=DF+OD=8
∴A点坐标为:(4,8),
∵点A在反比例函数y=(x>0,k>0)的图象上,
∴k=4×8=32,
∴反比例函数的关系式为y=,
(2)∵将菱形ABCD向右平移,当点D落在反比例函数y=(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=,
x=,
∴OF′=,
∴FF′=﹣4=,
∴菱形ABCD平移的距离为:;
(3)如图2,∵点P在x轴上,当点A,B,P不在同一条直线上时,点A,B,P构成三角形,
∴|PA﹣PB|<AB,
∴当点A,B,P在同一条直线上时,|PA﹣PB|最大,
由(1)知,A(4,8),
由菱形的性质得到B(0,5),
设直线AB的方程为:y=ax+b(a≠0),则
,
解得,
故直线AB的方程为:y=x+5,
令y=0,则0=x+5,
∴x=﹣,
∴P(﹣,0).
23.解:(1)∵一次函数y=﹣x+b的图象交x轴于B,交y轴于C,则B(b,0),C(0,b),
∴OB=OC=﹣b,
∵∠BOC=90°
∴△OBC是等腰直角三角形,
∴∠BCO=45°.
(2)如图1中,作MN⊥AB于N.
∵M(0,4),MN⊥AC,直线AC的解析式为y=﹣x+b,
∴直线MN的解析式为y=x+4,
由,解得,
∴N(,),
∵MA=MB,MN⊥AB,
∴NA=BN,设A(m,n),
则有,解得,
∴A(﹣4,b+4),
∵点A在y=﹣上,
∴﹣4(b+4)=﹣4,
∴b=﹣3,
∴A(﹣4,1).
(3)如图2中,
由(2)可知A(﹣4,1),M(0,4),
∴AM==5,
当菱形以AM为边时,AQ=AQ′=5,AQ∥OM,可得Q(﹣4,﹣4),Q′(﹣4,6),
当A,Q关于y轴对称时,也满足条件,此时Q(4,1)
当AM为菱形的对角线时,设P″(0,b),
则有(4﹣b)2=42+(b﹣1)2,
∴b=﹣.
∴AQ″=MP″=,
∴Q″(﹣4,),
综上所述,满足条件的点Q坐标为(﹣4,﹣4)或(﹣4,6)或(﹣4,)或(4,1).
