变量之间的关系【第六章回顾与思考】[下学期]
文档属性
| 名称 | 变量之间的关系【第六章回顾与思考】[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 33.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-25 21:56:00 | ||
图片预览




文档简介
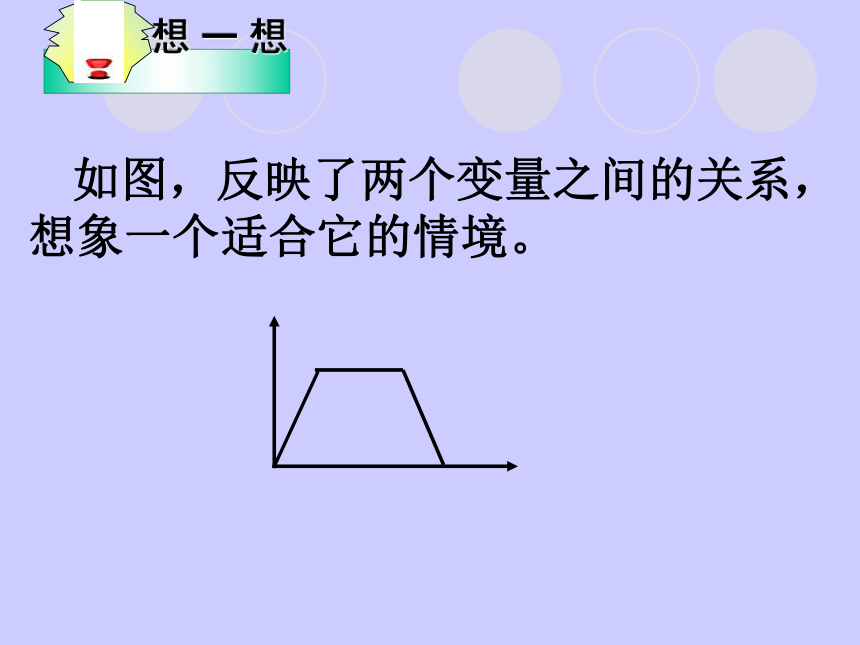
课件13张PPT。变量之间的关系 回顾与思考 如图,反映了两个变量之间的关系,想象一个适合它的情境。 小明给小颖打电话,按时收费,前3分钟收费0.2元,以后每增加1分钟(不足1分按1分计)加收0.1元,他们通话10分钟,
在这个过程中 发生了变化,自变量是 ,
因变量是 ,你能用哪些方法表示这些变量之间的关系呢? 1、弹簧秤的长度随着 的变化而变化,弹簧秤不挂重物时的长度是5厘米,每增加1千克的重量,弹簧秤的长度就会增加0.5厘米,当弹簧秤的长度是7.5厘米时
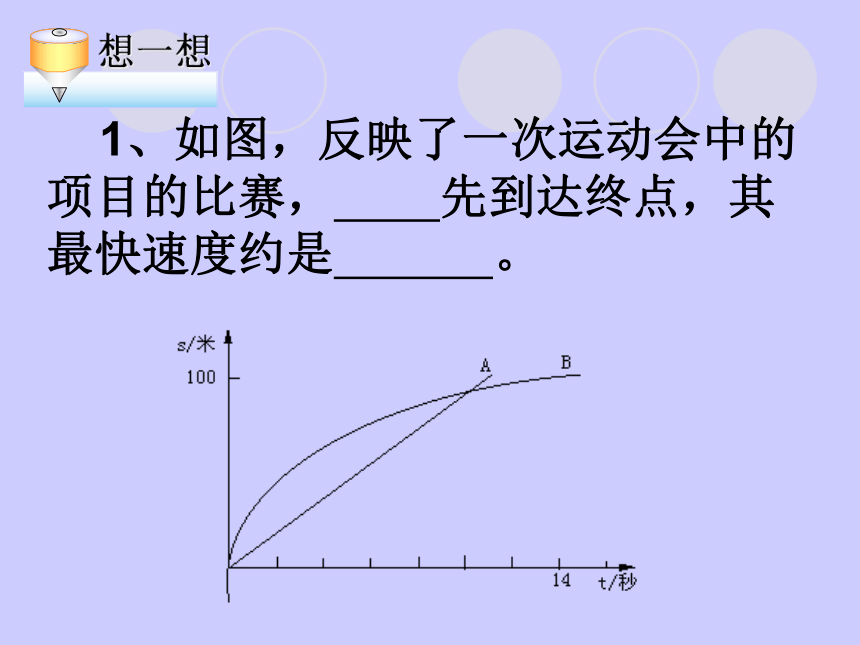
,物体重 千克。2.梯形的上底长是4厘米,下底长是10厘米,则梯形的面积s与高h 之间的关系式是 ,当h = 6厘米时,y = 厘米,当y = 140厘米时,h = 厘米。 1、如图,反映了一次运动会中的 项目的比赛, 先到达终点,其最快速度约是 。 2.如图,我国人口统计图如下:人口总数随着时间的变化趋势是 ,估计2009年我国人口总数大概是 。3.小明放学步行回家,从学校回家行走了一段时间后停下来买了一瓶可乐,然后又开始往家走直到回到家,
其步行的路程与时间的关系的图象大致是 ( )4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )5. 一个竖直向上抛出的乒乓球球,上升到最高点,又竖直下落,直到地面,又被反弹,上升到最高点,又竖直下落,反复好几次,直到停在地面上,
在此过程中,球的高度与时间的关系大致是 ( ) 6.小颖向平静的湖面扔了一粒石子,水面上出现了一圈一圈的水波,如图:
(1)观察这些水波随着时间的变化如何变化?
(2)在这个变化过程中,找出因变量和自变量;
(3)设圆的面积为s ,半径为r ,当半径从1厘米变化到5厘米时,面积如何变化? 西瓜的价格随着季节的变化而变化,变化情况如下图:
(1)大约是什么时候价格最便宜,价格是多少?
(2)大约是什么时候价格最贵,价格是多少?
(3)在什么时间范围内价格在增长?增长了多少?
(4)A 点和B点分别表示什么? 自变量dT=10-d/150因变量T在地球某地,温度T(C)
与高度d(m)的关系可以近
似地用T=10-d/150来表示,
根据这个关系式,当d的值
分别是0,200,400,600,
800,1000时,计算相应的
T值,并用表格表示所得结果。10.008.677.336.004.673.33
在这个过程中 发生了变化,自变量是 ,
因变量是 ,你能用哪些方法表示这些变量之间的关系呢? 1、弹簧秤的长度随着 的变化而变化,弹簧秤不挂重物时的长度是5厘米,每增加1千克的重量,弹簧秤的长度就会增加0.5厘米,当弹簧秤的长度是7.5厘米时
,物体重 千克。2.梯形的上底长是4厘米,下底长是10厘米,则梯形的面积s与高h 之间的关系式是 ,当h = 6厘米时,y = 厘米,当y = 140厘米时,h = 厘米。 1、如图,反映了一次运动会中的 项目的比赛, 先到达终点,其最快速度约是 。 2.如图,我国人口统计图如下:人口总数随着时间的变化趋势是 ,估计2009年我国人口总数大概是 。3.小明放学步行回家,从学校回家行走了一段时间后停下来买了一瓶可乐,然后又开始往家走直到回到家,
其步行的路程与时间的关系的图象大致是 ( )4.一壶正在烧的水,水的温度与时间的关系的图象大致是 ( )5. 一个竖直向上抛出的乒乓球球,上升到最高点,又竖直下落,直到地面,又被反弹,上升到最高点,又竖直下落,反复好几次,直到停在地面上,
在此过程中,球的高度与时间的关系大致是 ( ) 6.小颖向平静的湖面扔了一粒石子,水面上出现了一圈一圈的水波,如图:
(1)观察这些水波随着时间的变化如何变化?
(2)在这个变化过程中,找出因变量和自变量;
(3)设圆的面积为s ,半径为r ,当半径从1厘米变化到5厘米时,面积如何变化? 西瓜的价格随着季节的变化而变化,变化情况如下图:
(1)大约是什么时候价格最便宜,价格是多少?
(2)大约是什么时候价格最贵,价格是多少?
(3)在什么时间范围内价格在增长?增长了多少?
(4)A 点和B点分别表示什么? 自变量dT=10-d/150因变量T在地球某地,温度T(C)
与高度d(m)的关系可以近
似地用T=10-d/150来表示,
根据这个关系式,当d的值
分别是0,200,400,600,
800,1000时,计算相应的
T值,并用表格表示所得结果。10.008.677.336.004.673.33
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
