1.6整式的乘法（三）[下学期]

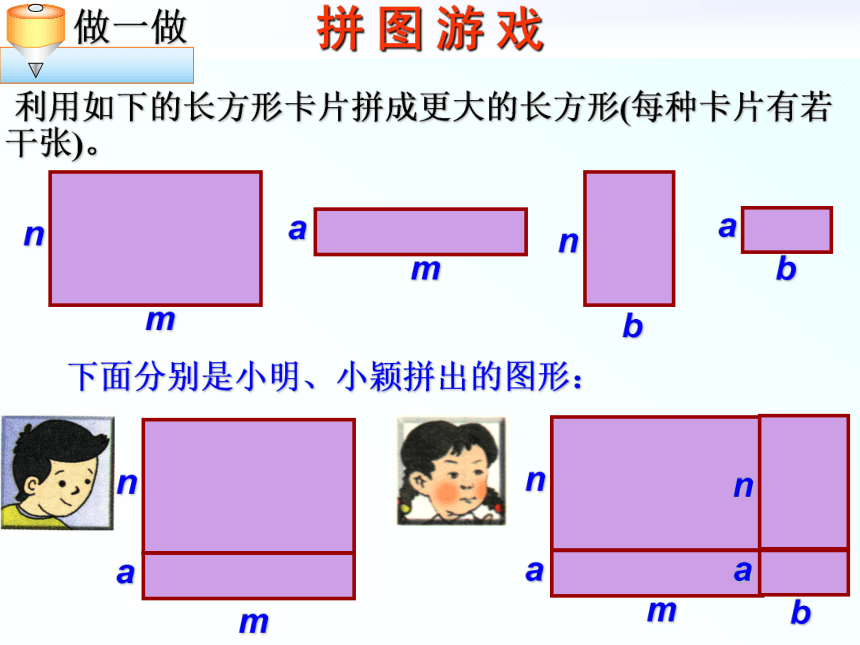
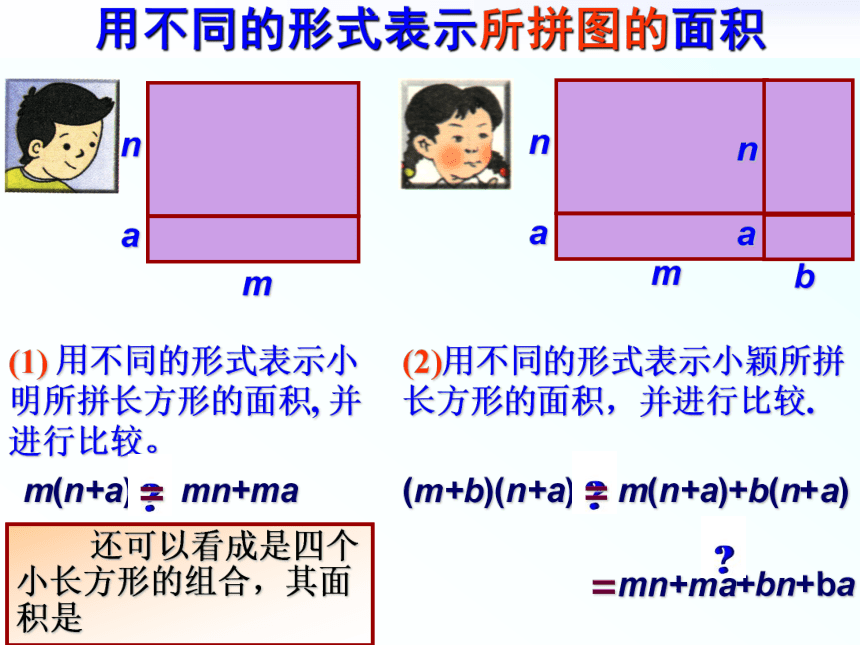
课件12张PPT。回顾与思考?② 再把所得的积相加。① 用单项式分别去乘多项式的每一项，单项式乘以多项式的 依据是 ; 乘法对加法的分配律.① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定.拼 图 游 戏 利用如下的长方形卡片拼成更大的长方形(每种卡片有若干张)。mnmabnba下面分别是小明、小颖拼出的图形：用不同的形式表示所拼图的面积(1) 用不同的形式表示小明所拼长方形的面积, 并进行比较。m(n+a)(2)用不同的形式表示小颖所拼长方形的面积，并进行比较.mn+ma=(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba==可以看成是小明拼的图形与另一个长方形的组合，其面积是 还可以看成是四个小长方形的组合，其面积是(m+b)(n+a)=m(n+a) + b(n+a) 的 理解(m+b)(n+a)、m(n+a)+b(n+a) ，
这些不同的式子都表示了最大
的长方形的面识，应该相等。 能用
“单项式乘以多项式”
来理解这两个式子的相等吗？?我们早已具备了“用字母表示数”概念，
故“x”可以表示一个数。“x”还可以表示 。一个单项式一个多项式将等号两端的 x换成(n+a)则有：(n+a)(n+a)(n+a)用乘法分配律 完成(m+b)(n+a)的计算把 m(n+a) 与 b(n+a) 看成
两个单项式与多项式相乘的运算，
应用单项式乘多项式的法则，(m+b)(n+a)=m(n+a) + b(n+a) 得:=mn+ma++bn+bamn+ ma+ ma+ bn+ bn 如何进行多项式与多项式相乘的运算 ？ 先用一个多项式的每一项
乘另一个多项式的每一项再把所得的积相加。(m+b)(n+a)=m(n+a) + b (n+a)mn+ ma+ ma+ bn+ bn例题解析例题解析 【例3】计算： 阅读 ? 体验 ? (1)(1?x)(0.6?x)； (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定：??1?x?x? 0.6+=0.6?1.6x+x2 ； ??x? x负负得正
一正一负得负。（2） (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. 随堂练习p28(1)(m+2n)(m?2n)； (2)(2n +5)(n?3) ;1、计算：(3)(x+2y)2 ; (4)(ax+b)(cx+d ) .接拓展练习本节课你的收获是什么？小结本节课你学到了什么?多项式乘以多项式的 依据是什么？如何进行多项式与多项式乘法运算？运用多项式乘法法则，要有序地逐项相乘，不要漏乘，并注意项的符号．最后的计算结果要化简￣￣￣合并同类项． 拓 展 练 习计算：(1) (x+30)(x+40)； (2) (x+30)(x?40)． 含有相同字母的两个一次二项式的乘积，是同一个字母的二次三项式 ：二次项是这个相同字母的平方(x2)；一次项系数是两个常数的和，常数项是两个常数的积．(x+a)(x+b)＝x2+(a+b)x+ab祝同学们学习愉快！