2022-2023学年京改版数学九年级上册 19.3 二次函数的性质 课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年京改版数学九年级上册 19.3 二次函数的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 614.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 09:04:41 | ||
图片预览






文档简介
(共18张PPT)
19.3二次函数的性质
教学目标
1.会用将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2.会熟练求出二次函数的顶点坐标、对称轴、最大(小)值.
3.会熟练描述二次函数的开口方向、增减性.
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1 , -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
1.完成下列表格:
复习导入
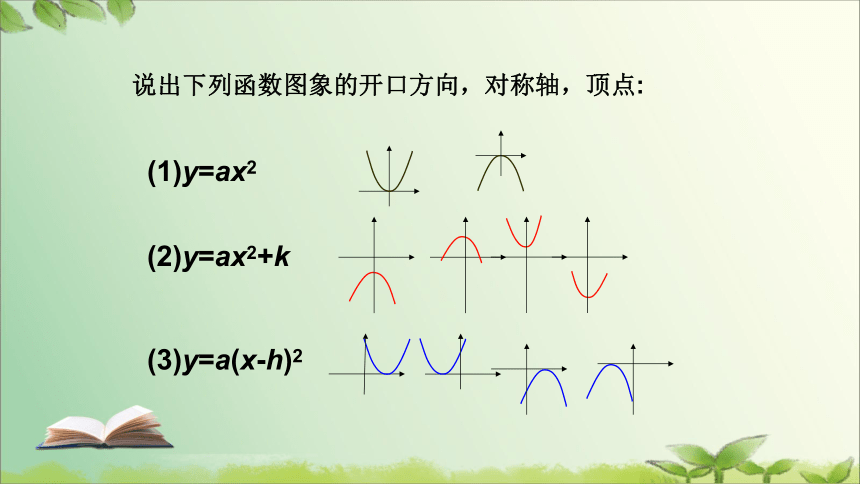
说出下列函数图象的开口方向,对称轴,顶点:
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2
将抛物线y=ax 沿y轴方向平移k个单位,得抛物线 y =ax +k 上+下-
将抛物线y=ax 沿x轴方向平移h个单位,得抛物线
y=a(x-h)2 左+右-
请说出二次函数y=2(x-3)2与抛物线 y=2x2 +3 如何由y=2x2 平移而来.
请说出二次函数y=ax +k与y=ax 的平移关系.
y=a(x-h)2与y=ax 的平移关系
拋物线y=2x2向右平移3个单位得y=2(x-3)2
拋物线y=2x2向上平移3个单位得y=2x2 +3
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x -h)2+k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax2+k
向左(右)平移|h|个单位
平移方法:
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
二次函数y=ax2+bx+c(a≠0)的性质:
观察二次函数 y= x2
y= (x-3)2 –4 图象:
探索新知
由特殊到一般,再由一般到特殊
试一试:
y=ax2+bx+c(a>0)
当x= 时,
若 x< ,则y随x的增大而减小
(反向变化);左高右低。
若 x≥ ,则 y随x的增大而增大
(同向变化);左低右高。
观察二次函数y= -x2的图像
做一做:
试一试:
y=ax2+bx+c(a<0)
若x≥ ,则y随x的增大而减小
(反向变化);左高右低 。
当 时,
若 x< ,则y随x的增大而增大
(同向变化);左低右高。
应用举例
何时取得最大值?
y随的变化怎样变化?
解:∵a= ,b=1,c=
∴对称轴x=
y= 2(x+3)2-2
画出下列函数图象,并说出抛物线的最值各是什么及增减性如何?
y= 2(x-3)2+3
y= 2(x-2)2-1
y= 3(x+1)2+1
巩固练习
画出二次函数y=-x2-4x-5的图像,并指出它的最大值或最小值.
分析:要画出二次函数y=-x2-4x-5的图像,可先将函数表达式变形为y=a(x+h)2+k的形式.
解: y=-x2-4x-5
=-(x2+4x+4-4)-5
=-(x+2)2-1.
二次项系数-1<0,函数图像开口向下,顶点坐标是(-2,-1),对称轴是过点(-2,-1)且平行于y轴的直线.
二次函数y=-x2-4x-5的图像如图所示.
当x=-2时,y有最大值,最大值是-1.
函数y= ax2+bx+c
Ⅰ、当a>0时:
当
最小值=
函数y= ax2+bx+c
Ⅱ、当a<0时
当
最大值=
通过配方,写出下列抛物线的增减性和最值.
(1)y=2x2+4x; (2)y=-2x2-3x;
(3)y=-3x2+6x-7; (4) y=x2-4x+5.
当a>0时,抛物线y=a(x-h)2+k的对称轴是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,函数取得最 值,这个值等于 ;
当a<0时,抛物线y=a (x-h)2+k,对称轴是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,函数取得最 值,这个值等于 .
h
k
x=h
小
增大
减小
h
大
k
x=h
减小
增大
谢 谢 !
19.3二次函数的性质
教学目标
1.会用将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.
2.会熟练求出二次函数的顶点坐标、对称轴、最大(小)值.
3.会熟练描述二次函数的开口方向、增减性.
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
向上
( 1 , -2 )
向下
向下
( 3 , 7)
( 2 , -6 )
向上
直线x=-3
直线x=1
直线x=3
直线x=2
(-3, 5 )
y=-3(x-1)2-2
y = 4(x-3)2+7
y=-5(2-x)2-6
1.完成下列表格:
复习导入
说出下列函数图象的开口方向,对称轴,顶点:
(1)y=ax2
(2)y=ax2+k
(3)y=a(x-h)2
将抛物线y=ax 沿y轴方向平移k个单位,得抛物线 y =ax +k 上+下-
将抛物线y=ax 沿x轴方向平移h个单位,得抛物线
y=a(x-h)2 左+右-
请说出二次函数y=2(x-3)2与抛物线 y=2x2 +3 如何由y=2x2 平移而来.
请说出二次函数y=ax +k与y=ax 的平移关系.
y=a(x-h)2与y=ax 的平移关系
拋物线y=2x2向右平移3个单位得y=2(x-3)2
拋物线y=2x2向上平移3个单位得y=2x2 +3
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x -h)2+k.平移的方向、距离要根据h、k的值来决定.
向左(右)平移|h|个单位
向上(下)平移|k|个单位
y=ax2
y=a(x-h)2
y=a(x-h)2+k
y=ax2
y=a(x-h)2+k
向上(下)平移|k|个单位
y=ax2+k
向左(右)平移|h|个单位
平移方法:
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上;
当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点是(h,k).
二次函数y=ax2+bx+c(a≠0)的性质:
观察二次函数 y= x2
y= (x-3)2 –4 图象:
探索新知
由特殊到一般,再由一般到特殊
试一试:
y=ax2+bx+c(a>0)
当x= 时,
若 x< ,则y随x的增大而减小
(反向变化);左高右低。
若 x≥ ,则 y随x的增大而增大
(同向变化);左低右高。
观察二次函数y= -x2的图像
做一做:
试一试:
y=ax2+bx+c(a<0)
若x≥ ,则y随x的增大而减小
(反向变化);左高右低 。
当 时,
若 x< ,则y随x的增大而增大
(同向变化);左低右高。
应用举例
何时取得最大值?
y随的变化怎样变化?
解:∵a= ,b=1,c=
∴对称轴x=
y= 2(x+3)2-2
画出下列函数图象,并说出抛物线的最值各是什么及增减性如何?
y= 2(x-3)2+3
y= 2(x-2)2-1
y= 3(x+1)2+1
巩固练习
画出二次函数y=-x2-4x-5的图像,并指出它的最大值或最小值.
分析:要画出二次函数y=-x2-4x-5的图像,可先将函数表达式变形为y=a(x+h)2+k的形式.
解: y=-x2-4x-5
=-(x2+4x+4-4)-5
=-(x+2)2-1.
二次项系数-1<0,函数图像开口向下,顶点坐标是(-2,-1),对称轴是过点(-2,-1)且平行于y轴的直线.
二次函数y=-x2-4x-5的图像如图所示.
当x=-2时,y有最大值,最大值是-1.
函数y= ax2+bx+c
Ⅰ、当a>0时:
当
最小值=
函数y= ax2+bx+c
Ⅱ、当a<0时
当
最大值=
通过配方,写出下列抛物线的增减性和最值.
(1)y=2x2+4x; (2)y=-2x2-3x;
(3)y=-3x2+6x-7; (4) y=x2-4x+5.
当a>0时,抛物线y=a(x-h)2+k的对称轴是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,函数取得最 值,这个值等于 ;
当a<0时,抛物线y=a (x-h)2+k,对称轴是 ,在对称轴的左侧,y随x的增大而 ,在对称轴的右侧,y随x的增大而 ,
当x= 时,函数取得最 值,这个值等于 .
h
k
x=h
小
增大
减小
h
大
k
x=h
减小
增大
谢 谢 !
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
