人教版2022-2023学年九年级数学上册 22.1.3 二次函数y=ax?+k的图象和性质同步精品 课件(共33张PPT)
文档属性
| 名称 | 人教版2022-2023学年九年级数学上册 22.1.3 二次函数y=ax?+k的图象和性质同步精品 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
二次函数y=ax2+k的图象和性质
1.会画二次函数y=ax2+k的图象.(重点)
2.掌握二次函数y=ax2+k的性质并会应用.(难点)
3.理解y=ax 与 y=ax +k之间的联系.(重点)
向上
向下
(0,0)
(0,0)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
方向
向上
向下
大小
越小
越大
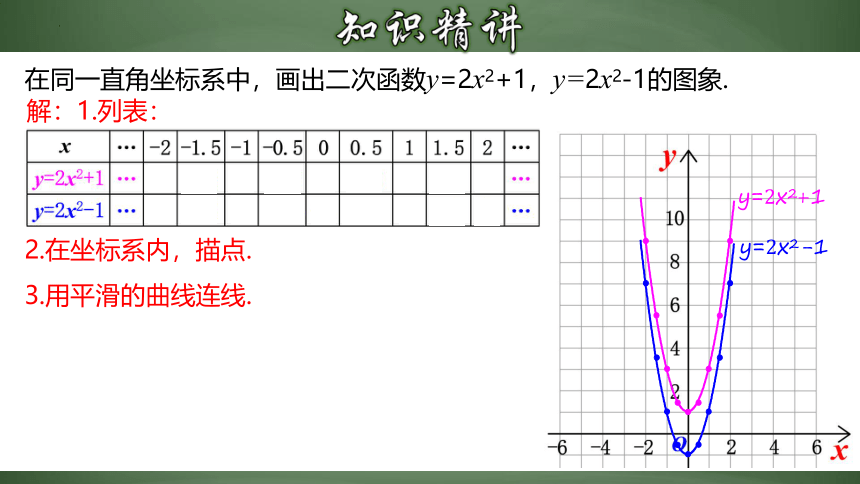
在同一直角坐标系中,画出二次函数y=2x2+1,y=2x2-1的图象.
解:1.列表:
2.在坐标系内,描点.
3.用平滑的曲线连线.
y=x2+1
y=x2-1
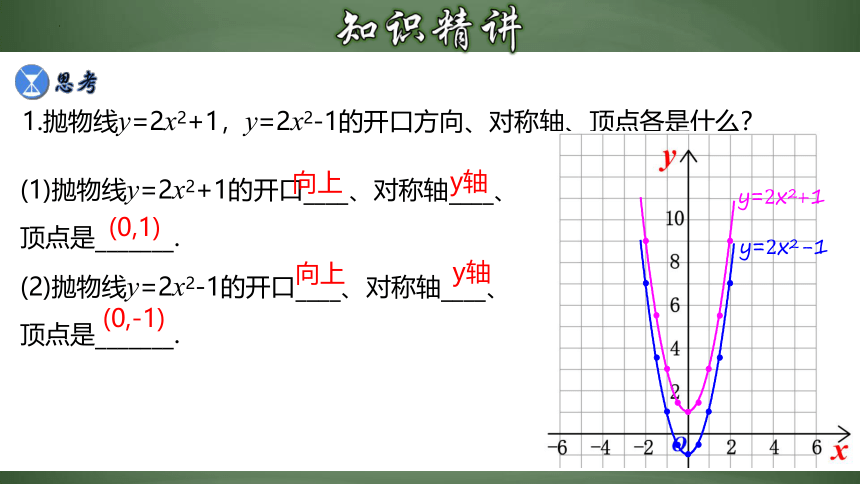
1.抛物线y=2x2+1,y=2x2-1的开口方向、对称轴、顶点各是什么?
y=x2+1
y=x2-1
(1)抛物线y=2x2+1的开口____、对称轴____、顶点是_______.
(2)抛物线y=2x2-1的开口____、对称轴____、顶点是_______.
向上
y轴
(0,1)
向上
y轴
(0,-1)
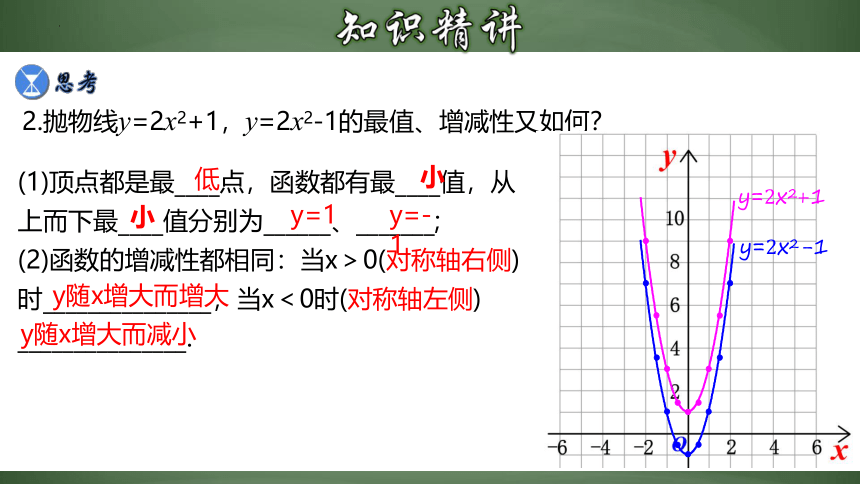
2.抛物线y=2x2+1,y=2x2-1的最值、增减性又如何?
y=x2+1
y=x2-1
(1)顶点都是最____点,函数都有最____值,从上而下最____值分别为______、_______;
(2)函数的增减性都相同:当x>0(对称轴右侧)时_______________,当x<0时(对称轴左侧) _______________.
低
小
y=1
y=-1
y随x增大而增大
y随x增大而减小
小
3.抛物线y=ax2+k(a>0)的图象有哪些性质?
一般地,当a>0时,抛物线y=ax2+k的开口向上,对称轴是y轴,顶点是(0,k),顶点是抛物线的最低点,函数有最小值,最小值为k.
在对称轴的左侧,抛物线从左到右下降趋势;在对称轴的右侧,抛物线从左到右上升趋势.也就是说,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
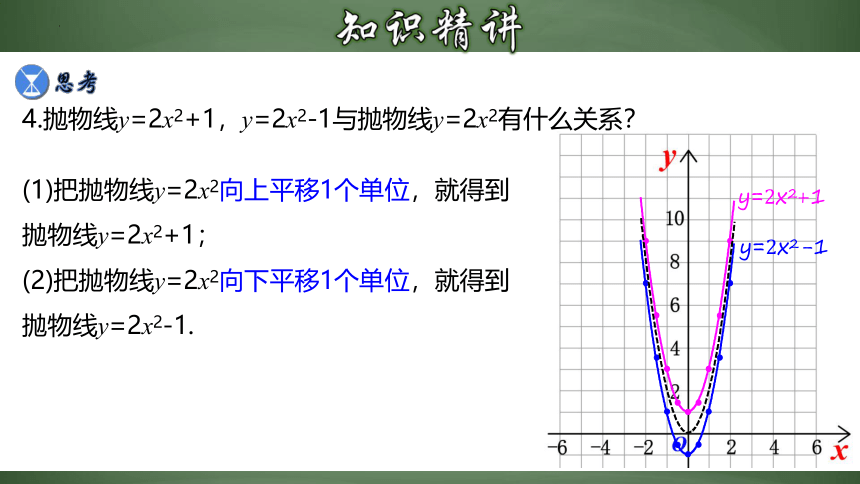
4.抛物线y=2x2+1,y=2x2-1与抛物线y=2x2有什么关系?
y=x2+1
y=x2-1
(1)把抛物线y=2x2向上平移1个单位,就得到抛物线y=2x2+1;
(2)把抛物线y=2x2向下平移1个单位,就得到抛物线y=2x2-1.
5.抛物线y=ax2+k与抛物线y=ax2有什么关系?
y=ax2
向上平移
k个单位
y=ax2+k(k>0)
y=ax2
向下平移
k个单位
y=ax2-k(k>0)
口决:上加下减
画出二次函数 , , 的图象,并考虑它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性.
根据图象回答下列问题:
(1)图象的形状都是 ;
(2)三条抛物线的开口方向_______;
(3)对称轴都是__________;
(4) 从上而下顶点坐标分别是
___________________;
抛物线
向下
y轴
(0,0)
(0,2)
(0,-2)
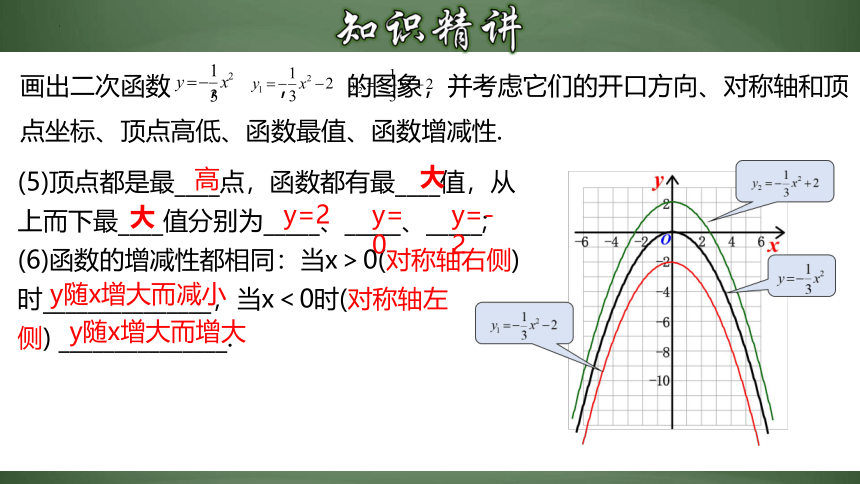
画出二次函数 , , 的图象,并考虑它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性.
(5)顶点都是最____点,函数都有最____值,从上而下最____值分别为_____、_____、_____;
(6)函数的增减性都相同:当x>0(对称轴右侧)时_______________,当x<0时(对称轴左
侧) _______________.
高
大
y=2
y=0
y随x增大而增大
y随x增大而减小
大
y=-2
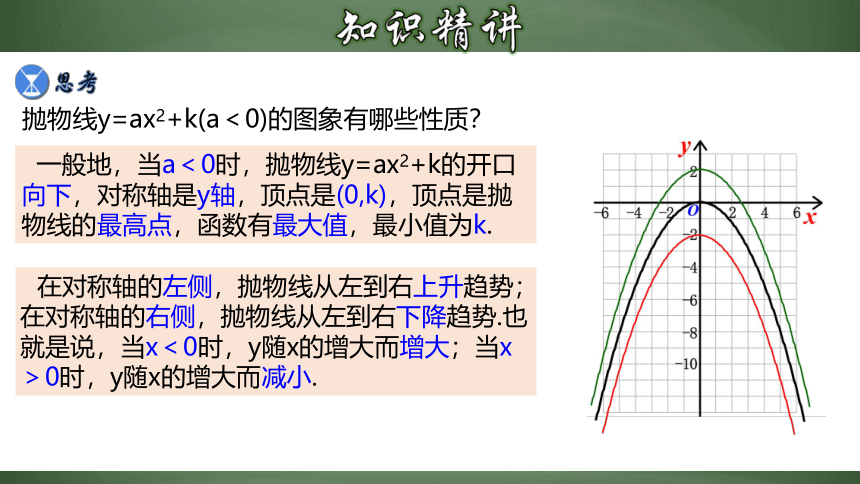
抛物线y=ax2+k(a<0)的图象有哪些性质?
一般地,当a<0时,抛物线y=ax2+k的开口向下,对称轴是y轴,顶点是(0,k),顶点是抛物线的最高点,函数有最大值,最小值为k.
在对称轴的左侧,抛物线从左到右上升趋势;在对称轴的右侧,抛物线从左到右下降趋势.也就是说,当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
二次函数y=ax2+k(a≠0)的性质
向上
向下
(0,k)
(0,k)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
例1.已知抛物线y=ax2+b过点(-2,-3)和点(1,6).
(1)求这个函数的关系式;
(2)写出当x为何值时,函数y随x的增大而增大.
解:(1)∵抛物线y=ax2+b过点(-2,-3)和点(1,6).
∴ ,解得
∴这个函数得关系式为:y=-3x2+9.
(2)∵二次函数y=-3x2+9开口向下,对称轴为y轴(x=0),
∴当x<0时,函数y随x的增大而增大.
二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),
(1)求函数y=ax2+c的表达式.
(2)若点C(-2,m),D(n ,7)也在函数的图象上,求点C的坐标;点D的坐标.
解:(1)将A(1,-1),B(2,5)代入y=ax2+c得:
,解得: ,
则二次函数解析式为y=2x2-3;
(2)将x=-2,y=m代入二次函数解析式得:y=m=5,即C(5,-2);
将x=n,y=7代入二次函数解析式得:7=2n2-3,即n= ,
即D( ,7)或( ,7).
例2.已知点A(-1,y1),B(-2,y2),C(4,y3)在二次函数y=-x2+c的图象上,则y1,y2 ,y3的大小关系是( )
A.y3<y2<y1 B.y2<y3<y1 C.y1<y2<y3 D.y1<y3<y2
【分析】解:∵y=-x2+c的开口向下,对称轴为直线x=0,
∴离对称轴越近函数值越大,
∵点A(-1,y1),B(-2,y2),C(4,y3)在二次函数y=-x2+c的图象上,
∴|-1|<|-2|<4,
∴y3<y2<y1.
A
1.已知二次函数y=x2-1图象上三点(-1,y1),(2,y2),(3,y3)比较y1,y2 ,y3的大小( )
A.y1<y3<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y1
B
2.若点A(-1,m)和B(-2,n)在二次函数y=-x2+20图象上,则m____n(填大小关系)
3.已知点A(1,y1),点B(2,y2)在二次函数y=ax2-2(a≠0)的图象上,且y1<y2,那么a的取值范围是______.
>
a>0
例3.已知函数 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
解:(1)∵函数 是关于x的二次函数,
∴m2+m-4=2,
解得:m1=2,m2=-3;
(2)当m=2时,抛物线有最低点,
此时y=4x2+1,
则最低点为:(0,1),
由于抛物线的对称轴为y轴,故当x>0时,y随x的增大而增大;
例3.已知函数 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
解:(3)当m=﹣3时,函数有最大值,
此时y=-x2+1,故此函数有最大值1,
由于抛物线的对称轴为y轴,
故当x>0时,y随x的增大而减小.
1.已知二次函数 ,下列说法正确的是( )
A.图象开口向上 B.图象的顶点坐标为(-2,3)
C.图象的对称轴是直线x=-3 D.有最大值,为-3
D
2.二次函数 的图象开口向上,则k=_____.
例4.已知二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x=x1+x2时,其函数值为________.
【分析】由二次函数y=ax2+c图象的性质可知,x1,x2关于y轴对称,即x1+x2=0.把x=0代入二次函数表达式求出纵坐标为c.
c
【点睛】二次函数y=ax2+c的图象关于y轴对称,因此左右两部分折叠可以重合,函数值相等的两点的对应横坐标互为相反数.
x
y
O
-2
2
2
4
6
4
-4
8
二次函数y=-2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,当x=x1+x2时,对应的函数值y=___.
1
例5.函数y=ax-a和y=ax2+2(a为常数,且a≠0),在同一平面直角坐标系中的大致图象可能是( )
A B C D
C
【分析】解:由y=ax2+2的顶点坐标为(0,2), 故A,B不符合题意;
由C,D中二次函数的图象可得:a<0,
∴-a>0,
∴函数y=ax-a过一,二,四象限,故C符合题意,D不符合题意,
在同一直角从标系中,一次函数y=ax+c和二次函数y=ax2+c.的图象大致是如图中的( )
B
例6.如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴ ×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=± ,
此时P点坐标为( ,2),(- ,2);
当b=-2时,x2-4=-2,解得x=± ,
此时P点坐标为( ,2),(- ,2).
典例解析
1.若将抛物线y=-2x2-2的图象的顶点移到原点,则下列平移方法正确的是( )
A.向上平移2个单位 B.向下平移2个单位
C.向左平移2个单位 D.向右平移2个单位
2.当a<0时,函数y=ax2+a的图象经过的象限是( )
A.第三、四象限 B.第一、二象限
C.第二、三、四象限 D.第一、三象限
A
A
3.抛物线y=-3x2-2的开口方向是_____,顶点坐标是_______,对称轴是____,
抛物线y=-3x2-2可由抛物线y=-3x2向____平移____个单位得到.
4.若拋物线y=ax2-1经过点(4,31),则a=____,在这个函数图象上该点关于对称轴对称的点为_________.
向下
(0,-2)
y轴
下
2
2
(-4,31)
6.将抛物线y=x2-1向上平移2个单位,则此时抛物线的解析式是_________.
5.抛物线y=-4x2+8的开口______,对称轴是______,顶点坐标是_______,抛物线与x轴的交点坐标__________________,与y轴的交点坐标______,当x<0时,y随着x的增大而_____,当x>0时,y随着x的增大而______,当______________时,y>0.
向下
(0,8)
y轴
(,0)、(,0)
(0,8)
增大
减小
<
y=x2+1
7.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
D
8.已知二次函数y=ax2与y=-2x2+c.
(1)随着系数a和c的变化,分别说出这两个二次函数图象的变与不变;
(2)若这两个函数图象的形状相同,则a=____;若抛物线y=ax2沿y轴向下平移2个单位就能与y=-2x2+c的图象完全重合,则c=_____;
(3)二次函数y=-2x2+c中x、y的几组对应值如表:
表中m、n、p的大小关系为__________(用“<”连接).
x -2 1 5
y m n p
解:(1)二次函数y=ax2的图象随着a的变化,开口大小和开口方向都会变化,但是对称轴、顶点坐标不会改变;二次函数y=-2x2+c的图象随着c的变化,开囗大小和开口方向都没有改变,对称轴也没有改变,但是,顶点坐标会发生改变;
(2)∵函数y=ax2与函数y=-2x2+c的形状相同,
∴a=±2,
∵抛物线y=ax2沿y轴向下平移2个单位得到y=ax2-2,与y=-2x2+c的图象完全重合,
∴c=-2,
(3)由函数y=﹣2x2+c可知,抛物线开口向下,对称轴为y轴,
∵1﹣0<0﹣(﹣2)<5﹣0,
∴p<m<n,
二次函数y=ax2+k(a≠0)的性质
向上
向下
(0,k)
(0,k)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
二次函数y=ax2+k的图象和性质
1.会画二次函数y=ax2+k的图象.(重点)
2.掌握二次函数y=ax2+k的性质并会应用.(难点)
3.理解y=ax 与 y=ax +k之间的联系.(重点)
向上
向下
(0,0)
(0,0)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
方向
向上
向下
大小
越小
越大
在同一直角坐标系中,画出二次函数y=2x2+1,y=2x2-1的图象.
解:1.列表:
2.在坐标系内,描点.
3.用平滑的曲线连线.
y=x2+1
y=x2-1
1.抛物线y=2x2+1,y=2x2-1的开口方向、对称轴、顶点各是什么?
y=x2+1
y=x2-1
(1)抛物线y=2x2+1的开口____、对称轴____、顶点是_______.
(2)抛物线y=2x2-1的开口____、对称轴____、顶点是_______.
向上
y轴
(0,1)
向上
y轴
(0,-1)
2.抛物线y=2x2+1,y=2x2-1的最值、增减性又如何?
y=x2+1
y=x2-1
(1)顶点都是最____点,函数都有最____值,从上而下最____值分别为______、_______;
(2)函数的增减性都相同:当x>0(对称轴右侧)时_______________,当x<0时(对称轴左侧) _______________.
低
小
y=1
y=-1
y随x增大而增大
y随x增大而减小
小
3.抛物线y=ax2+k(a>0)的图象有哪些性质?
一般地,当a>0时,抛物线y=ax2+k的开口向上,对称轴是y轴,顶点是(0,k),顶点是抛物线的最低点,函数有最小值,最小值为k.
在对称轴的左侧,抛物线从左到右下降趋势;在对称轴的右侧,抛物线从左到右上升趋势.也就是说,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
4.抛物线y=2x2+1,y=2x2-1与抛物线y=2x2有什么关系?
y=x2+1
y=x2-1
(1)把抛物线y=2x2向上平移1个单位,就得到抛物线y=2x2+1;
(2)把抛物线y=2x2向下平移1个单位,就得到抛物线y=2x2-1.
5.抛物线y=ax2+k与抛物线y=ax2有什么关系?
y=ax2
向上平移
k个单位
y=ax2+k(k>0)
y=ax2
向下平移
k个单位
y=ax2-k(k>0)
口决:上加下减
画出二次函数 , , 的图象,并考虑它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性.
根据图象回答下列问题:
(1)图象的形状都是 ;
(2)三条抛物线的开口方向_______;
(3)对称轴都是__________;
(4) 从上而下顶点坐标分别是
___________________;
抛物线
向下
y轴
(0,0)
(0,2)
(0,-2)
画出二次函数 , , 的图象,并考虑它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性.
(5)顶点都是最____点,函数都有最____值,从上而下最____值分别为_____、_____、_____;
(6)函数的增减性都相同:当x>0(对称轴右侧)时_______________,当x<0时(对称轴左
侧) _______________.
高
大
y=2
y=0
y随x增大而增大
y随x增大而减小
大
y=-2
抛物线y=ax2+k(a<0)的图象有哪些性质?
一般地,当a<0时,抛物线y=ax2+k的开口向下,对称轴是y轴,顶点是(0,k),顶点是抛物线的最高点,函数有最大值,最小值为k.
在对称轴的左侧,抛物线从左到右上升趋势;在对称轴的右侧,抛物线从左到右下降趋势.也就是说,当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
二次函数y=ax2+k(a≠0)的性质
向上
向下
(0,k)
(0,k)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
例1.已知抛物线y=ax2+b过点(-2,-3)和点(1,6).
(1)求这个函数的关系式;
(2)写出当x为何值时,函数y随x的增大而增大.
解:(1)∵抛物线y=ax2+b过点(-2,-3)和点(1,6).
∴ ,解得
∴这个函数得关系式为:y=-3x2+9.
(2)∵二次函数y=-3x2+9开口向下,对称轴为y轴(x=0),
∴当x<0时,函数y随x的增大而增大.
二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),
(1)求函数y=ax2+c的表达式.
(2)若点C(-2,m),D(n ,7)也在函数的图象上,求点C的坐标;点D的坐标.
解:(1)将A(1,-1),B(2,5)代入y=ax2+c得:
,解得: ,
则二次函数解析式为y=2x2-3;
(2)将x=-2,y=m代入二次函数解析式得:y=m=5,即C(5,-2);
将x=n,y=7代入二次函数解析式得:7=2n2-3,即n= ,
即D( ,7)或( ,7).
例2.已知点A(-1,y1),B(-2,y2),C(4,y3)在二次函数y=-x2+c的图象上,则y1,y2 ,y3的大小关系是( )
A.y3<y2<y1 B.y2<y3<y1 C.y1<y2<y3 D.y1<y3<y2
【分析】解:∵y=-x2+c的开口向下,对称轴为直线x=0,
∴离对称轴越近函数值越大,
∵点A(-1,y1),B(-2,y2),C(4,y3)在二次函数y=-x2+c的图象上,
∴|-1|<|-2|<4,
∴y3<y2<y1.
A
1.已知二次函数y=x2-1图象上三点(-1,y1),(2,y2),(3,y3)比较y1,y2 ,y3的大小( )
A.y1<y3<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y1
B
2.若点A(-1,m)和B(-2,n)在二次函数y=-x2+20图象上,则m____n(填大小关系)
3.已知点A(1,y1),点B(2,y2)在二次函数y=ax2-2(a≠0)的图象上,且y1<y2,那么a的取值范围是______.
>
a>0
例3.已知函数 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
解:(1)∵函数 是关于x的二次函数,
∴m2+m-4=2,
解得:m1=2,m2=-3;
(2)当m=2时,抛物线有最低点,
此时y=4x2+1,
则最低点为:(0,1),
由于抛物线的对称轴为y轴,故当x>0时,y随x的增大而增大;
例3.已知函数 是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
解:(3)当m=﹣3时,函数有最大值,
此时y=-x2+1,故此函数有最大值1,
由于抛物线的对称轴为y轴,
故当x>0时,y随x的增大而减小.
1.已知二次函数 ,下列说法正确的是( )
A.图象开口向上 B.图象的顶点坐标为(-2,3)
C.图象的对称轴是直线x=-3 D.有最大值,为-3
D
2.二次函数 的图象开口向上,则k=_____.
例4.已知二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x=x1+x2时,其函数值为________.
【分析】由二次函数y=ax2+c图象的性质可知,x1,x2关于y轴对称,即x1+x2=0.把x=0代入二次函数表达式求出纵坐标为c.
c
【点睛】二次函数y=ax2+c的图象关于y轴对称,因此左右两部分折叠可以重合,函数值相等的两点的对应横坐标互为相反数.
x
y
O
-2
2
2
4
6
4
-4
8
二次函数y=-2x2+1的图象上有两点A(x1,y1)、B(x2,y2),且x1≠x2,y1=y2,当x=x1+x2时,对应的函数值y=___.
1
例5.函数y=ax-a和y=ax2+2(a为常数,且a≠0),在同一平面直角坐标系中的大致图象可能是( )
A B C D
C
【分析】解:由y=ax2+2的顶点坐标为(0,2), 故A,B不符合题意;
由C,D中二次函数的图象可得:a<0,
∴-a>0,
∴函数y=ax-a过一,二,四象限,故C符合题意,D不符合题意,
在同一直角从标系中,一次函数y=ax+c和二次函数y=ax2+c.的图象大致是如图中的( )
B
例6.如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.
解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴ ×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=± ,
此时P点坐标为( ,2),(- ,2);
当b=-2时,x2-4=-2,解得x=± ,
此时P点坐标为( ,2),(- ,2).
典例解析
1.若将抛物线y=-2x2-2的图象的顶点移到原点,则下列平移方法正确的是( )
A.向上平移2个单位 B.向下平移2个单位
C.向左平移2个单位 D.向右平移2个单位
2.当a<0时,函数y=ax2+a的图象经过的象限是( )
A.第三、四象限 B.第一、二象限
C.第二、三、四象限 D.第一、三象限
A
A
3.抛物线y=-3x2-2的开口方向是_____,顶点坐标是_______,对称轴是____,
抛物线y=-3x2-2可由抛物线y=-3x2向____平移____个单位得到.
4.若拋物线y=ax2-1经过点(4,31),则a=____,在这个函数图象上该点关于对称轴对称的点为_________.
向下
(0,-2)
y轴
下
2
2
(-4,31)
6.将抛物线y=x2-1向上平移2个单位,则此时抛物线的解析式是_________.
5.抛物线y=-4x2+8的开口______,对称轴是______,顶点坐标是_______,抛物线与x轴的交点坐标__________________,与y轴的交点坐标______,当x<0时,y随着x的增大而_____,当x>0时,y随着x的增大而______,当______________时,y>0.
向下
(0,8)
y轴
(,0)、(,0)
(0,8)
增大
减小
<
y=x2+1
7.在同一直角坐标系中,一次函数y=ax+k和二次函数y=ax2+k的图象大致为( )
D
8.已知二次函数y=ax2与y=-2x2+c.
(1)随着系数a和c的变化,分别说出这两个二次函数图象的变与不变;
(2)若这两个函数图象的形状相同,则a=____;若抛物线y=ax2沿y轴向下平移2个单位就能与y=-2x2+c的图象完全重合,则c=_____;
(3)二次函数y=-2x2+c中x、y的几组对应值如表:
表中m、n、p的大小关系为__________(用“<”连接).
x -2 1 5
y m n p
解:(1)二次函数y=ax2的图象随着a的变化,开口大小和开口方向都会变化,但是对称轴、顶点坐标不会改变;二次函数y=-2x2+c的图象随着c的变化,开囗大小和开口方向都没有改变,对称轴也没有改变,但是,顶点坐标会发生改变;
(2)∵函数y=ax2与函数y=-2x2+c的形状相同,
∴a=±2,
∵抛物线y=ax2沿y轴向下平移2个单位得到y=ax2-2,与y=-2x2+c的图象完全重合,
∴c=-2,
(3)由函数y=﹣2x2+c可知,抛物线开口向下,对称轴为y轴,
∵1﹣0<0﹣(﹣2)<5﹣0,
∴p<m<n,
二次函数y=ax2+k(a≠0)的性质
向上
向下
(0,k)
(0,k)
y轴
y轴
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,
y最小=0.
当x=0时,
y最大=0.
同课章节目录
