2022-2023学年九年级数学上册 23.2.2 中心对称图形 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年九年级数学上册 23.2.2 中心对称图形 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 09:29:41 | ||
图片预览






文档简介
(共24张PPT)
人教版九年级(上)数学教学课件
第23章 旋转
23.2.2 中心对称图形
情境导入
探究新知
当堂训练
典例精讲
知识归纳
情境导入
温故知新
中心对称图形
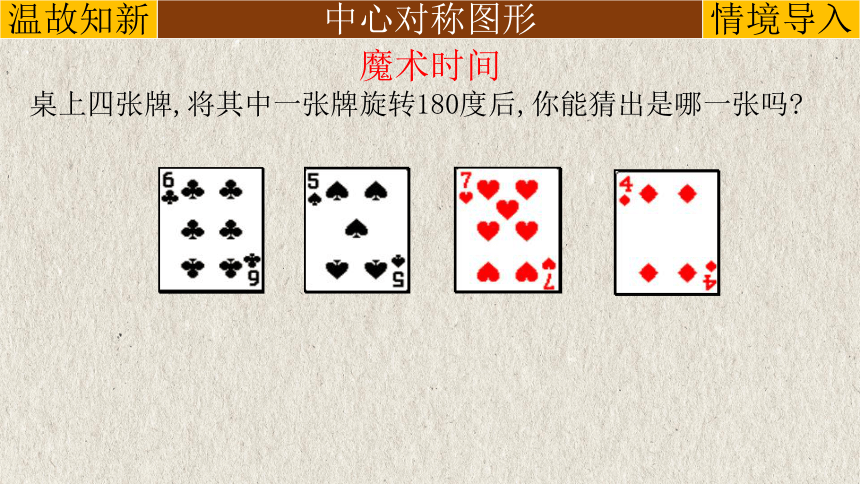
魔术时间
桌上四张牌,将其中一张牌旋转180度后,你能猜出是哪一张吗
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
A
B
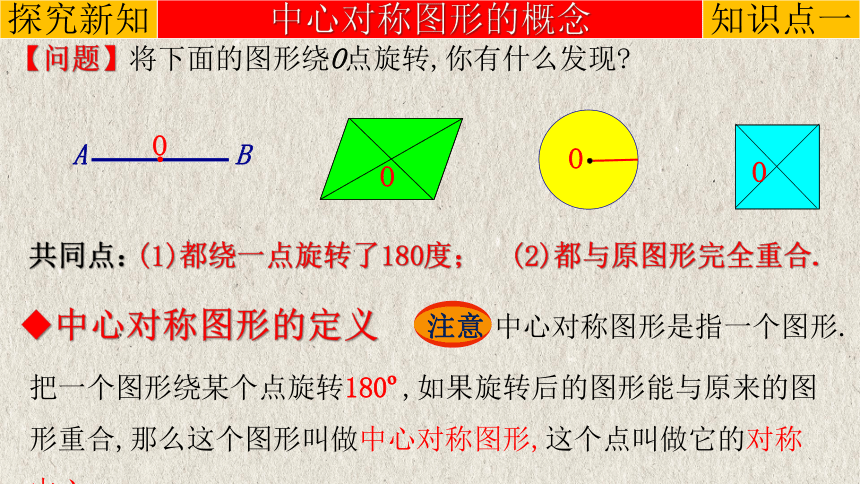
【问题】将下面的图形绕O点旋转,你有什么发现
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
O
O
知识点一
探究新知
中心对称图形的概念
把一个图形绕某个点旋转180 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
中心对称图形的定义
中心对称图形是指一个图形.
注意
图(1)
图(2)
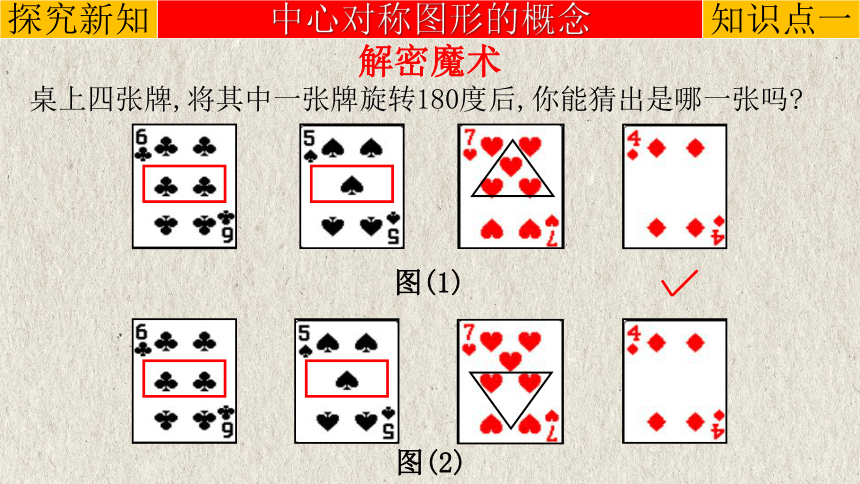
解密魔术
桌上四张牌,将其中一张牌旋转180度后,你能猜出是哪一张吗
知识点一
探究新知
中心对称图形的概念
(1)
(2)
(3)
【例1】下列图形中哪些是中心对称图形吗?
√
√
√
√
√
(6)
(5)
(4)
√
(7)
×
知识点一
典例精讲
中心对称图形的概念
1.在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2.在线段、角、等腰三角形、等边三角形、等腰梯形、平行四边形、矩形、菱形、正方形、正六边形、圆中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
D
知识点二
针对训练
中心对称图形的性质
B
A
C
D
B
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
D
知识点一
针对训练
中心对称图形的概念
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
探究中心对称图形的性质
A
B
D
C
O
(1)中心对称图形的对称点
连线都经过__________
(2)中心对称图形的对称点
连线被_____________
对称中心
对称中心平分
中心对称图形上的每一对对称点的连线都经过对称中心且被对称中心平分.
知识点二
探究新知
中心对称图形的性质
性质:
中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别
联系
3.对称点在两个图形上
1.针对一个图形而言的
1.针对两个图形而言的
2.是指两个图形的(位置)关系
4.对称中心在两个图形之间
4.对称中心在图形上或其内部
3.对称点在一个图形上
2.是指具有某种性质的一个图形
把成中心对称的两个图形视为一个整体,则是中心对称图形;
把中心对称图形的两部分看做两个图形,则它们成中心对称
知识点二
知识归纳
中心对称图形的性质
【例2】如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为___.
3
知识点二
典例精讲
中心对称图形的性质
A
O
F
E
B
C
D
1.如图,有一个平行四边形请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎么画?
知识点二
针对训练
中心对称图形的性质
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳:
割法2
补法
(若上边是灌溉用的水渠的一岸.每块土地都要有水渠,怎么平分土地才能满足每个人的需要?)
割法1
2.如图,水渠旁有一大块L形耕地,要画一条直线为分界线,把耕地平均分成两块,分别承包给两个人,应该怎样分 有几种分法
知识点二
拓展提升
中心对称图形的性质
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
【问题1】正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
(2)边数为偶数的正多边形既是轴对称图形,也是中心对称图形.
(1)边数为奇数的正多边形都是轴对称图形.
知识点三
探究新知
正多边形的旋转对称
(3)正多边形还具有旋转对称的特点.
【问题2】正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?
旋转90
旋转180
旋转270
旋转360
正方形是中心对称图形;它绕两条对角线的交点旋转90 或其整数倍,都能与原来的图形重合,
因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。
知识点三
探究新知
正多边形的旋转对称
(1) 绕着它的中心旋转多少度的整数倍后所得的三角形与原来的三角形重合
120 的整数倍.
90 的整数倍.
72 的整数倍.
1.问题探究
2.概念引入
把正n边形绕着它的中心旋转 的整数倍后所得的正n边形与原正n边形重合,我们说,正n边形关于其中心有 的旋转对称.一般地,如果一个图形绕着某点O旋转角α后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.
旋转对称
正三角形
正 方 形
正五边形
知识点三
知识归纳
正多边形的旋转对称
3.深化思考
(1)旋转对称一定是正多边形吗
不一定都是正多边形. (比如:圆)
中心对称图形可以看成是有180°的旋转对称.
圆是任意角的旋转对称.
(2)中心对称图形和旋转图形有什么关系
(3)圆作为旋转对称有什么特点
知识点三
知识归纳
正多边形的旋转对称
1.正方形是中心对称图形,绕它的中心,旋转一周和原来的图形重合___次.
2.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点;
②每次旋转了____度;
③一共旋转了____次.
4
60
5
知识点三
针对训练
正多边形的旋转对称
O
中心对称 中心对称图形
定义
性质
区别
联系
中心对称图形与中心对称图形有什么区别与联系?
把一个图形绕着某一个点旋转180 ,若它能够与另一个图形重合,那么这两个图形关于这点对称,
若一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,
①两个图形全等;
②对称点的连线都经过对称中心,
并且被对称中心平分
中心对称图形的对称点都经过对称中心,并且被对称中心平分.
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
知识梳理
课堂小结
中心对称图形
强
化
训
练
1.如图,左边数字与右边数字成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2.请根据下面5个图形的特征,画出第6组图形_________.
D
①
②
③
④
提升能力
强化训练
中心对称图形
3.(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,
使4个阴影小正方形组
成一个既是轴对称图形,
又是中心对称图形.
图1
图2
图3
提升能力
强化训练
中心对称图形
×
人教版九年级(上)数学教学课件
第23章 旋转
23.2.2 中心对称图形
情境导入
探究新知
当堂训练
典例精讲
知识归纳
情境导入
温故知新
中心对称图形
魔术时间
桌上四张牌,将其中一张牌旋转180度后,你能猜出是哪一张吗
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
A
B
【问题】将下面的图形绕O点旋转,你有什么发现
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
O
O
知识点一
探究新知
中心对称图形的概念
把一个图形绕某个点旋转180 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
中心对称图形的定义
中心对称图形是指一个图形.
注意
图(1)
图(2)
解密魔术
桌上四张牌,将其中一张牌旋转180度后,你能猜出是哪一张吗
知识点一
探究新知
中心对称图形的概念
(1)
(2)
(3)
【例1】下列图形中哪些是中心对称图形吗?
√
√
√
√
√
(6)
(5)
(4)
√
(7)
×
知识点一
典例精讲
中心对称图形的概念
1.在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2.在线段、角、等腰三角形、等边三角形、等腰梯形、平行四边形、矩形、菱形、正方形、正六边形、圆中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
D
知识点二
针对训练
中心对称图形的性质
B
A
C
D
B
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
D
知识点一
针对训练
中心对称图形的概念
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
探究中心对称图形的性质
A
B
D
C
O
(1)中心对称图形的对称点
连线都经过__________
(2)中心对称图形的对称点
连线被_____________
对称中心
对称中心平分
中心对称图形上的每一对对称点的连线都经过对称中心且被对称中心平分.
知识点二
探究新知
中心对称图形的性质
性质:
中心对称与中心对称图形的区别与联系:
中心对称 中心对称图形
区别
联系
3.对称点在两个图形上
1.针对一个图形而言的
1.针对两个图形而言的
2.是指两个图形的(位置)关系
4.对称中心在两个图形之间
4.对称中心在图形上或其内部
3.对称点在一个图形上
2.是指具有某种性质的一个图形
把成中心对称的两个图形视为一个整体,则是中心对称图形;
把中心对称图形的两部分看做两个图形,则它们成中心对称
知识点二
知识归纳
中心对称图形的性质
【例2】如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为___.
3
知识点二
典例精讲
中心对称图形的性质
A
O
F
E
B
C
D
1.如图,有一个平行四边形请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎么画?
知识点二
针对训练
中心对称图形的性质
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳:
割法2
补法
(若上边是灌溉用的水渠的一岸.每块土地都要有水渠,怎么平分土地才能满足每个人的需要?)
割法1
2.如图,水渠旁有一大块L形耕地,要画一条直线为分界线,把耕地平均分成两块,分别承包给两个人,应该怎样分 有几种分法
知识点二
拓展提升
中心对称图形的性质
中心对称图形的概念
01
中心对称图形的性质
02
正多边形的旋转对称
03
知识要点
精讲精练
【问题1】正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边形呢?……你能发现什么规律?
(2)边数为偶数的正多边形既是轴对称图形,也是中心对称图形.
(1)边数为奇数的正多边形都是轴对称图形.
知识点三
探究新知
正多边形的旋转对称
(3)正多边形还具有旋转对称的特点.
【问题2】正方形是中心对称图形吗?正方形绕两条对角线的交点旋转多少度能与原来的图形重合?
旋转90
旋转180
旋转270
旋转360
正方形是中心对称图形;它绕两条对角线的交点旋转90 或其整数倍,都能与原来的图形重合,
因此,可以验证正方形的四边相等、四角相等、对角线互相垂直平分等性质。
知识点三
探究新知
正多边形的旋转对称
(1) 绕着它的中心旋转多少度的整数倍后所得的三角形与原来的三角形重合
120 的整数倍.
90 的整数倍.
72 的整数倍.
1.问题探究
2.概念引入
把正n边形绕着它的中心旋转 的整数倍后所得的正n边形与原正n边形重合,我们说,正n边形关于其中心有 的旋转对称.一般地,如果一个图形绕着某点O旋转角α后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.
旋转对称
正三角形
正 方 形
正五边形
知识点三
知识归纳
正多边形的旋转对称
3.深化思考
(1)旋转对称一定是正多边形吗
不一定都是正多边形. (比如:圆)
中心对称图形可以看成是有180°的旋转对称.
圆是任意角的旋转对称.
(2)中心对称图形和旋转图形有什么关系
(3)圆作为旋转对称有什么特点
知识点三
知识归纳
正多边形的旋转对称
1.正方形是中心对称图形,绕它的中心,旋转一周和原来的图形重合___次.
2.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点;
②每次旋转了____度;
③一共旋转了____次.
4
60
5
知识点三
针对训练
正多边形的旋转对称
O
中心对称 中心对称图形
定义
性质
区别
联系
中心对称图形与中心对称图形有什么区别与联系?
把一个图形绕着某一个点旋转180 ,若它能够与另一个图形重合,那么这两个图形关于这点对称,
若一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,
①两个图形全等;
②对称点的连线都经过对称中心,
并且被对称中心平分
中心对称图形的对称点都经过对称中心,并且被对称中心平分.
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成为中心对称图形。
知识梳理
课堂小结
中心对称图形
强
化
训
练
1.如图,左边数字与右边数字成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
2.请根据下面5个图形的特征,画出第6组图形_________.
D
①
②
③
④
提升能力
强化训练
中心对称图形
3.(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取1个涂上阴影,
使4个阴影小正方形组
成一个既是轴对称图形,
又是中心对称图形.
图1
图2
图3
提升能力
强化训练
中心对称图形
×
同课章节目录
