人教版2022-2023学年八年级数学上册同步备课系列 第十二章 全等三角形章节复习课件(共60张PPT)
文档属性
| 名称 | 人教版2022-2023学年八年级数学上册同步备课系列 第十二章 全等三角形章节复习课件(共60张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览



文档简介
(共60张PPT)
全等三角形章节复习
1.全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;
2.掌握全等三角形的判定条件,并能进行简单的证明和计算,掌握综合法证明的格式;
3.掌握角平分线的性质及判定,能利用三角形全等证明角的平分线的性质,会利用角的平分线的性质进行证明.
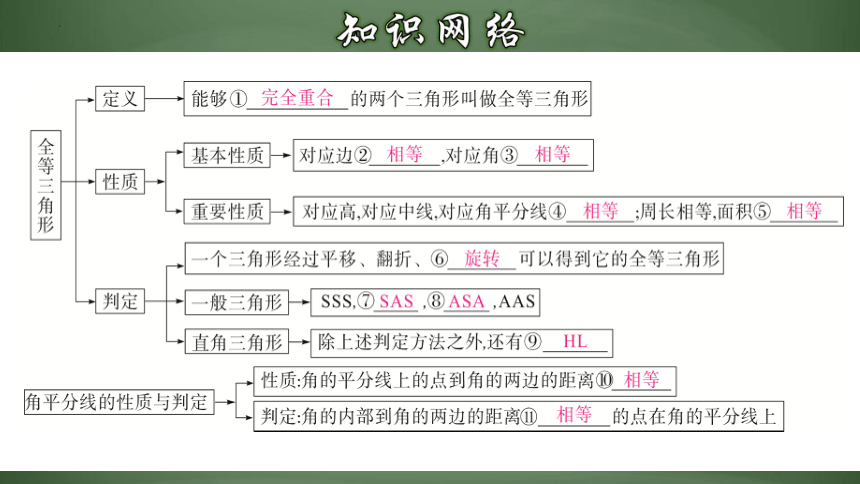
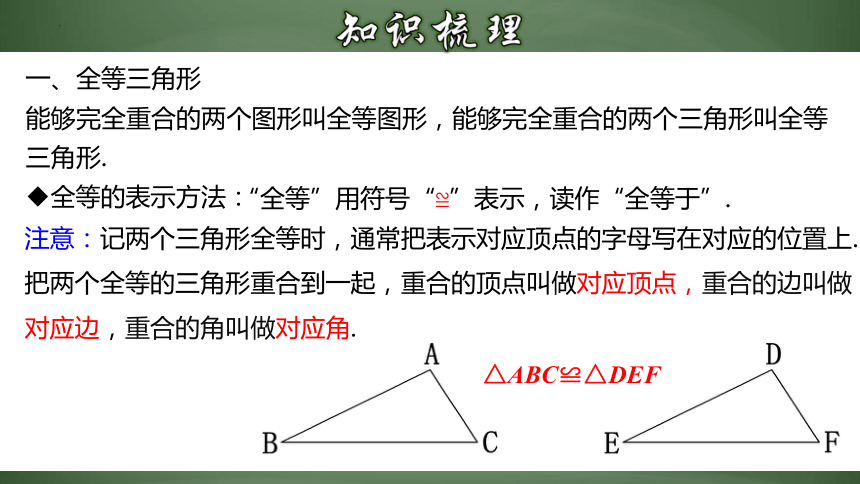
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
一、全等三角形
△ABC≌△DEF
全等的表示方法:
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
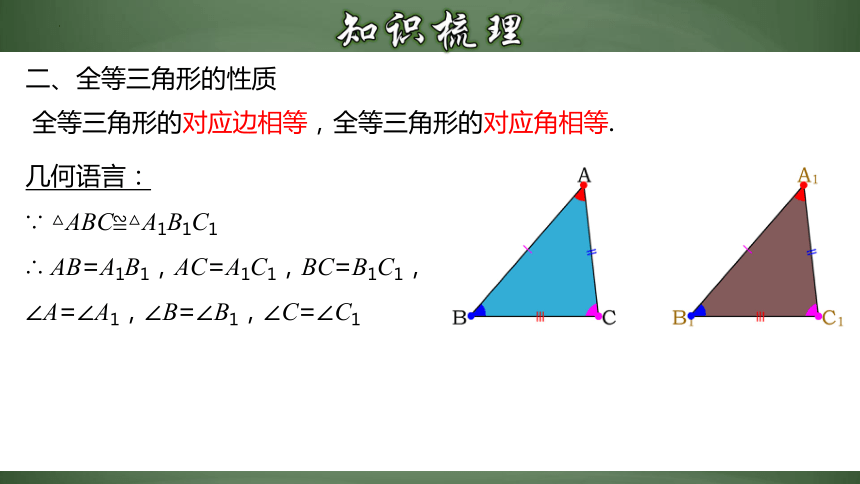
二、全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
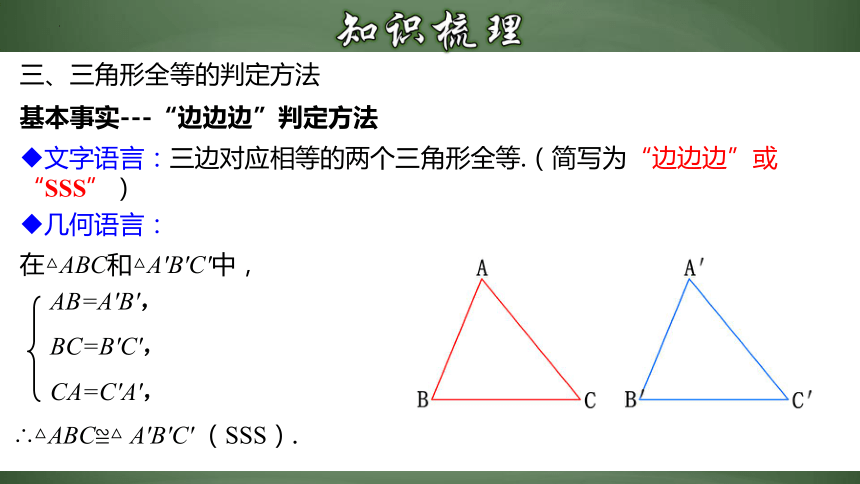
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
基本事实---“边边边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△ A′B′C′ (SSS).
AB=A′B′,
BC=B′C′,
CA=C′A′,
几何语言:
三、三角形全等的判定方法
证明两个三角形全等的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
三、三角形全等的判定方法
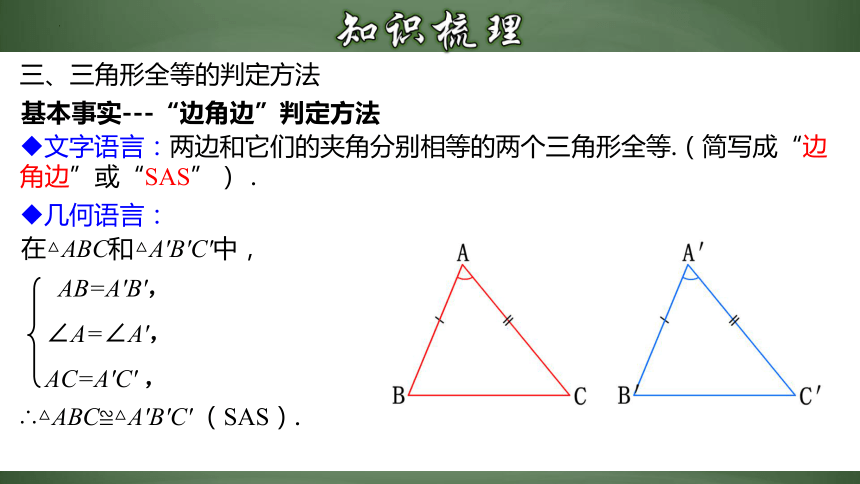
文字语言:两边和它们的夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”).
基本事实---“边角边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (SAS).
AB=A′B′,
∠A=∠A′,
AC=A′C′ ,
几何语言:
三、三角形全等的判定方法
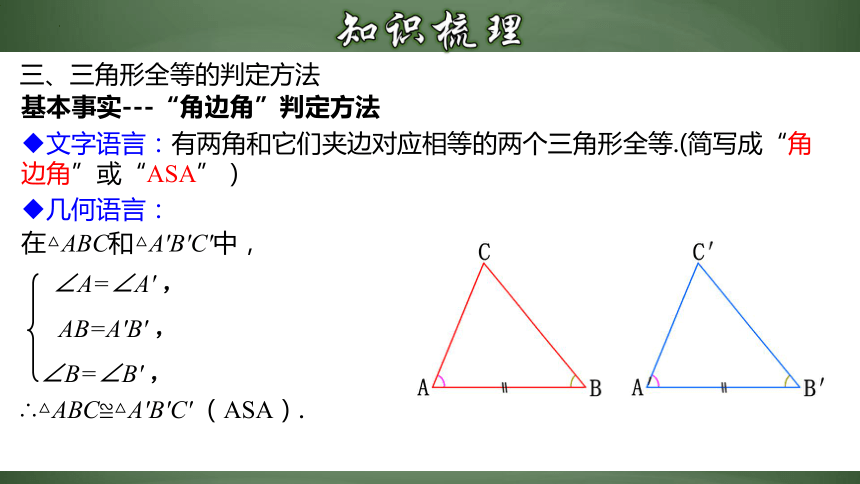
文字语言:有两角和它们夹边对应相等的两个三角形全等.(简写成“角边角”或“ASA”)
基本事实---“角边角”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
AB=A′B′ ,
∠B=∠B′ ,
几何语言:
三、三角形全等的判定方法
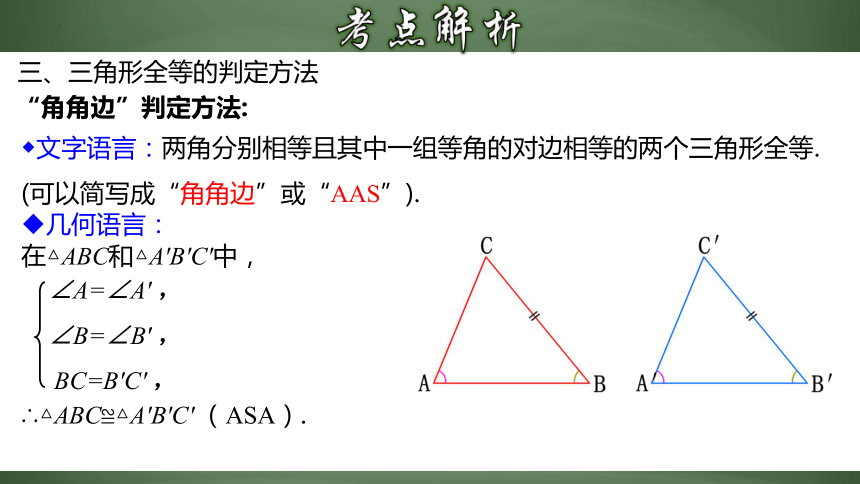
◆文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等.
(可以简写成“角角边”或“AAS”).
“角角边”判定方法:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
∠B=∠B′ ,
BC=B′C′ ,
几何语言:
三、三角形全等的判定方法
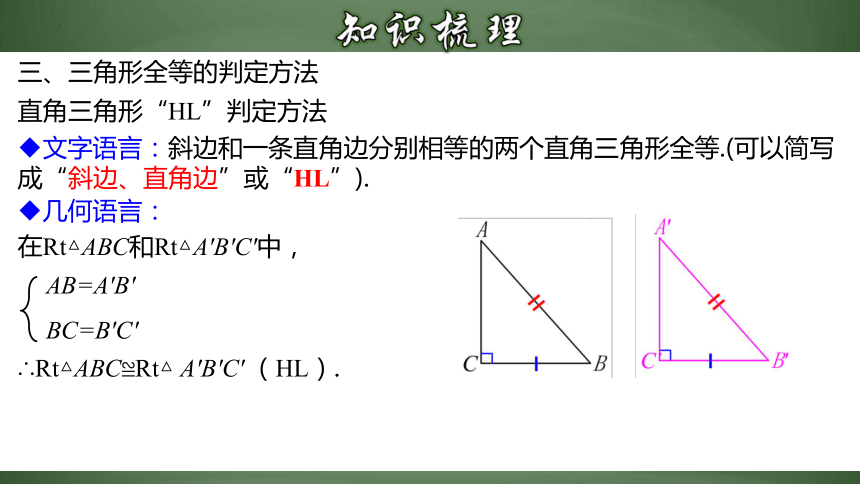
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
三、三角形全等的判定方法
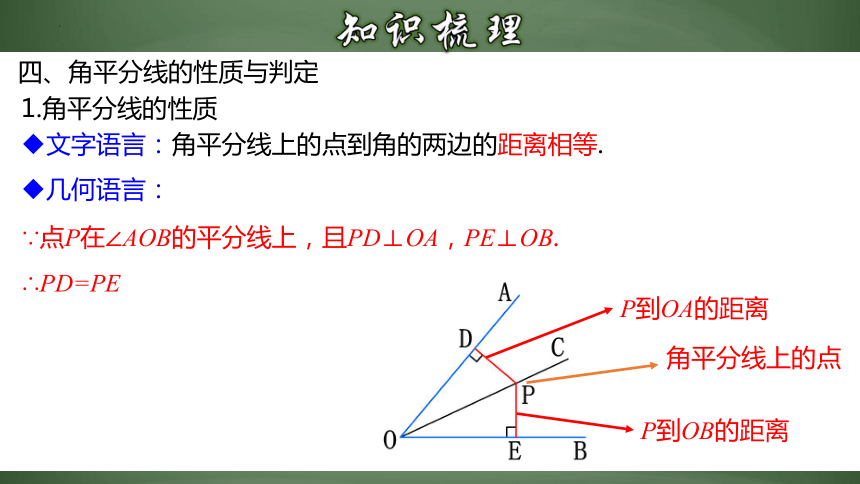
文字语言:角平分线上的点到角的两边的距离相等.
1.角平分线的性质
几何语言:
∵点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB.
∴PD=PE
P到OA的距离
P到OB的距离
角平分线上的点
四、角平分线的性质与判定
文字语言:角的内部到角的两边的距离相等的点在角的平分线上.
2.角的平分线的判定
几何语言:
∵ PD⊥OA于D,PE⊥OB于E,PD=PE,
∴点P 在∠AOB的平分线上.(或∠1=∠2)
四、角平分线的性质与判定
角的平分线的性质
图形
已知 条件
结论
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
全等三角形的性质
1
例1.如图△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
解: ∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D,
∵∠EAB=120°,∠CAD=10°,∠B=25°,
∴∠D=∠B=25°,
∠DAE=∠BAC=(∠EAB-∠CAD)=×(120°-10°)=55°,
∴∠DFB=∠FAB+∠B=∠CAD+∠CAB+∠B
=10°+55°+25°=90°,
∴∠DGB=∠DFB-∠D=90°-25°=65°,
∴∠DFB=90°, ∠DGB=65°.
全等三角形的性质
1
例2.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D ∥EB′ ∥BC ,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
C
H
全等三角形的性质
1
例3.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与△ABO全等,点P与点O不重合,写出符合条件的点P的坐标:_________.
解:设点P的坐标为(a,b),
∴A(2,0) ,B(2,4)
∴OA=2,AB=4,∠OAB=90°,
由题意,分以下两种情况:
(1)如图1,当△BAP≌△ABO时,
∴PB=OA=2,∠PBA=∠OAB=90°
∴PB∥x轴,
∴b=AB=4 ,
又∵PB=2 ,
=2 ,
解得a=4或a=0,
则此时点P的坐标为P(4,4)或P(0,4) ;
全等三角形的性质
1
例3.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与△ABO全等,点P与点O不重合,写出符合条件的点P的坐标:_________.
(2)如图2,当△ABP≌△ABO时,
∴PA=OA=2, ∠PAB=∠OAB=90°
∵点P在x轴上,且OP=OA+PA=4 ,
则此时点P的坐标为P(4,0);
综上,符合条件的点P的坐标为(4,4)或(0,4)或(4,0) ,
【1-1】如图,△ABC沿BC方向平移到△DEF的位置.
(1)若∠B=30°,∠F=45°,求∠A的度数;
(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=(BF-EC)=3,
∴平移的距离BE为3.
【1-2】如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为________厘米/秒.
1或1.6
【1-3】如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A.1 B.1或4 C.1或2 D.3
B
全等三角形的判定
2
例4.如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )
A.BC=BD; B.AC=AD;
C.∠ACB=∠ADB; D.∠CAB=∠DAB
B
全等三角形的判定
2
例5.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
全等三角形的判定
2
例5.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
全等三角形的判定
2
例6.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.
(1)请你找出图中其他的全等三角形;(2)试证明CF=EF.
解:(1)图中其它的全等三角形为:①△ACD≌△AEB,②△DCF≌△BEF;
②∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS).
全等三角形的判定
2
例6.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.(2)试证明CF=EF.
(2)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB(SAS),
∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS),
∴CF=EF.
【2-1】如图,已知∠B=∠DEC,AB=DE,要推得△ABC≌△DEC;
(1)若以“SAS”为依据,还缺条件______________;
(2)若以“ASA”为依据,还缺条件__________________;
(3)若以“AAS”为依据,还缺条件________________________________.
BC=EC
∠A=∠EDC
∠ACB=∠DCE (或∠ACD=∠BCE)
【2-2】如图,已知CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点0,且AO平分∠BAC,那么图中全等三角形共有______对.
4
【分析】根据条件: CD⊥AB,BE⊥AC ,AO平分∠BAC及隐含的条件AO=AO(公共边).
∴△ADO≌△AEO(AAS),∴AD=AE,
∴△ADC≌△AEB(ASA),∴∠B=∠C,
∴△ABO≌△ACO(AAS),∴BO=CO,∴△BDO≌△CEO(AAS),
∴图中全等三角形共有4对.
【2-3】如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS),
∴∠ABC=∠DEF.
①②④
③
【2-3】如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴AC=DF.
①③④
②
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
A
B
C
D
F
E
G
【分析】
欲证∠DEC=∠FEC
由平行线的性质转化为证明∠DEC=∠DCE
只需要证明△DEG≌△DCG.
全等三角形的性质与判定的综合应用
3
A
B
C
D
F
E
G
证明:∵CE⊥AD, ∴∠AGE=∠AGC=90°.
在△AGE和△AGC中,
∠AGE=∠AGC,
AG=AG,
∠EAG=∠CAG,
∴△AGE≌△AGC(ASA),
∴GE=GC.
∵AD平分∠BAC,∴∠EAG=∠CAG,.
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
全等三角形的性质与判定的综合应用
3
在△DGE和△DGC中,
EG=CG,
∠EGD=∠CGD=90°,
DG=DG.
∴△DGE≌△DGC(SAS).
∴∠DEG=∠DCG.
∵EF//BC,
∴∠FEC=∠ECD,
∴∠DEG=∠FEC.
【点睛】利用全等三角形证明角相等,首先要找到两个角所在的两个三角形,看它们全等的条件够不够;有时会用到等角转换,等角转换的途径很多,如:余角,补角的性质、平行线的性质等,必要时要想到添加辅助线.
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
A
B
C
D
F
E
G
全等三角形的性质与判定的综合应用
3
全等三角形的性质与判定的综合应用
3
例8.如图,在△ADC中,DB是高,点E是DB上一点,AB=DB,EB=CB,M,N分别是AE,CD上的点,且AM=DN;
(1)试说明:△ABE △DBC;
(2)探索BM和BN的位置关系和数量关系,并说明理由.
(1)证明:∵DB是△ADC的高,∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
AB=DB,∠ABE=∠DBC,BE=BC,∴△ABE △DBC.
全等三角形的性质与判定的综合应用
3
(2)BM=BN且BM⊥BN.理由如下:∵△ABE △DBC,∴∠BAM=∠BDN.
在△ABM和△DBN中,
AB=DB,∠BAM=∠BDN,AM=DN,
∴△ABM △DBN.
∴BM=BN,∠ABM=∠DBN.
∴∠DBN+∠DBM=∠ABM+∠DBM=∠ABD=90°,即BM⊥BN.
例8.如图,在△ADC中,DB是高,点E是DB上一点,AB=DB,EB=CB,M,N分别是AE,CD上的点,且AM=DN;
(1)试说明:△ABE △DBC;
(2)探索BM和BN的位置关系和数量关系,并说明理由.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明:DE=DF:
(2)在图中,若G在AB上且∠EDG=60°,试猜想
CE,EG,BG之间的数量关系并证明所归纳结论.
(3)若题中条件“∠CAB=60°,∠CDB=120°
改为∠CAB=α,∠CDB=180°﹣α,G在AB上,
∠EDG满足什么条件时,(2)中结论仍然成立?
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明:DE=DF:
证明∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°-60°-120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在ΔCDE和ΔBDF中,CD=BD,∠C=∠DBF,CE=BF
∴ΔCDE ΔBDF(SAS),
∴DE=DF.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.
解:如图,连接AD,
猜想CE、EG、BG之间的数量关系为:CE+BG=EG.
证明:在ΔABD和ΔACD中AB=AC,BD=CD,AD=AD ,
∴ΔABD ΔACD(SSS),
∴∠BDA=∠CDA=∠CDB=×120°=60°,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得ΔCDE ΔBDF,
全等三角形的性质与判定的综合应用
3
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在ΔDEG和ΔDFG中,DE=DF,∠EDG=∠FDG,DG=DG
∴ΔDEG ΔDFG(SAS),
∴EG=FG,
又∵CE=BF,FG=BF+BG,∴CE+BG=EG;
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(3)若题中条件“∠CAB=60°,∠CDB=120°改为∠CAB=α,∠CDB=
180°﹣α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?
解:要使CE+BG=EG仍然成立,
则∠EDG=∠BDA=∠CDA=∠CDB,
即∠EDG= (180°-α)=90°- α,
∴当∠EDG=90°- α时,CE+BG=EG仍然成立.
【3-1】如图:在ΔABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.
(1)求证:∠ABE=∠ACG;
(2)试判:AG与AD的关系?并说明理由.
(1)证明:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠AEB=90°,
∴∠ACG+∠FAC=∠FAC+∠ABE=90°,
∴∠ABE=∠ACG;
(2)解:AG=AD,AG⊥AD,理由如下:
由(1)可知:∠ABD=∠GCA,
∵BD=AC,AB=GC,
∴△ABD≌△GCA(SAS),
∴AG=AD,∠BAD=∠CGA,
∵∠AFG=90°,
∴∠CGA+∠GAF=90°,
∴∠BAD+∠GAF=90°,即∠GAD=90°,
∴AG⊥AD.
【3-2】如图1,∠DAB=90°,CD⊥AD于点D,点E是线段AD上的一点,若DE=AB,DC=AE.
(1)判断CE与BE的关系是____________.
(2)如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD,并保持CD=AE,DE=AB,连接CB,CE,BE,试说明(1)中结论是否成立,并说明理由.
(1)解:垂直且相等,理由如下:
∵CD⊥AD,∴∠D=90°,
在△EDC与△BAE中,
ED=AB,∠D=∠DAB,DC=AE ,
∴△EDC △BAE,
∴BE=CE,∠DCE=∠AEB,
∵∠DCE+∠DEC=90°,
∴∠DEC+∠AEB=90°,即∠CEB=90°,∴CE⊥BE,∴CE与BE的关系为:垂直且相等.
【3-2】如图1,∠DAB=90°,CD⊥AD于点D,点E是线段AD上的一点,若DE=AB,DC=AE.
(1)判断CE与BE的关系是____________.
(2)如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD,并保持CD=AE,DE=AB,连接CB,CE,BE,试说明(1)中结论是否成立,并说明理由.
(2)结论成立,理由如下:
∵CD⊥AD,∴∠D=90°,
在△EDC与△BAE中,ED=AB,∠D=∠DAB,DC=AE ,∴△EDC △BAE,
∴BE=CE,∠DCE=∠AEB,
∵∠DCE+∠DEC=90°,∴∠DEC+∠AEB=90°,即∠CEB=90°,∴CE⊥BE,
∴CE与BE的关系为:垂直且相等.
【3-3】如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED,
(1)如图,若∠A+∠EDC=180°,在五边形ABCDE的外部,作△EDF≌△EAB,(不写作法,只保留作图痕迹),并说明点C,D,F三点在同一直线上;
(2)如图,若∠A=60°,∠EDC=120°,且BC=AB+CD,求证:CE平分∠BCD.
(1)解:如图作∠FED=∠AEB,EB=EF,
∵EA=ED,
∴ΔAEB ΔDEF(SAS),
∴∠A=∠EDF,
∵∠A+∠CDE=180°,
∴∠CDE+∠EDF=180°,
∴C、D、F点在同一直线上,
【3-3】如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED,
(2)如图,若∠A=60°,∠EDC=120°,且BC=AB+CD,求证:CE平分∠BCD.
(2)延长CD到T,使得DT=BA,连接ET,
∵∠CDE=120°,
∴∠EDT=180°-120°=60°,
∵∠A=60°,
∴∠A=∠EDT,
在ΔEAB和ΔEDT中,
AE=DE,∠A=∠EDT,AB=DT,
∴ΔEAB ΔEDT(SAS),
∴EB=ET,
∴CB=CD+BA=CD+DT=CT,
在ΔECB和ΔECT中,
EC=EC,EB=ET,CB=CT,
∴ΔECB ΔECT(SSS),
∴∠ECB=∠ECD,
即EC平分∠BCD.
例10.如图,小明和小华家中间隔了一个办公楼,他们想要测量自己家对面办公楼的高OM,小明在自家阳台A处测得办公楼顶部O的仰角∠1,小华在自家阳台B处测得办公楼顶部O的仰角∠2.已知C,M,D三点共线,OA⊥OB且OA=OB,AC=10m,BD=3m,CD=17m.试求办公楼的高度OM.
利用全等三角形解决实际问题
4
解:过点A作AE⊥OM,过点B作BF⊥OM,如图所示,
∵OA⊥OB,AE⊥OM,BF⊥OM,
∴∠AOB=∠AEO=∠BFO=90°,
∴∠BOF+∠2=90°,∠AOE+∠BOF=90°,
∴∠2=∠AOE,
在 AOE与 BOF中,
∠AEO=∠BFO,∠AOE=∠2,OA=OB,
∴ AOE BOF
例10.如图,小明和小华家中间隔了一个办公楼,他们想要测量自己家对面办公楼的高OM,小明在自家阳台A处测得办公楼顶部O的仰角∠1,小华在自家阳台B处测得办公楼顶部O的仰角∠2.已知C,M,D三点共线,OA⊥OB且OA=OB,AC=10m,BD=3m,CD=17m.试求办公楼的高度OM.
利用全等三角形解决实际问题
4
∴OE=BF,AE=OF,
设OM=x,则OE=OM-EM=OM-AC=x-10,
∴BF=OE=x-10,
∵OF=OM-FM=OM-BD=x-3,
∴AE=CM=CD-MD=CD-BF=17-(x-10),
17-(x-10)=x-3,
解得:x=15,
即OM=15m.
【4-1】如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离相等吗?
A
B
C
D
【分析】将本题中的实际问题转化为数学问题就是证明BD=CD.由已知条件可知AB=AC,AD⊥BC.
解:相等,理由如下:
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
AD=AD,
AB=AC,
∴Rt△ADB ≌ Rt△ADC(HL).
∴BD=CD.
【4-2】如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?
解:要测量A、B间的距离,可用如下方法:
过点B作AB的垂线BF,在BF上取两点C、D,使CD=BC,
再作出BF的垂线DE,使A、C、E在一条直线上,
∵∠ACB=∠ECD,CB=CD,∠ABC=∠EDC,
∴△EDC≌△ABC(ASA).
∴DE=BA.
答:测出DE的长就是A、B之间的距离.
C
D
E
【4-3】如图是小明和爸爸妈妈在公园里荡秋千的示意图,小明坐在秋千的起始位置A处,OA与地面垂直,小明两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他.若妈妈与爸爸到OA的水平距离BD,CE分别为1.6m和2m,且∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由.
(2)爸爸是在距离地面多高的地方接住小明的?
(1)根据题意,得∠OEC=∠ODB=90°,OA=OB=OC
∴∠BOD+∠OBD=90°,∠COE+∠OCE=90°
∵∠BOC=90°
∴∠BOD+∠COE=90°
∴∠OCE=∠BOD
∴∠OEC=∠ODB,∠OCE=∠BOD,OC=OB
∴△COE≌△OBD;
【4-3】如图是小明和爸爸妈妈在公园里荡秋千的示意图,小明坐在秋千的起始位置A处,OA与地面垂直,小明两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他.若妈妈与爸爸到OA的水平距离BD,CE分别为1.6m和2m,且∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由.
(2)爸爸是在距离地面多高的地方接住小明的?
(2)结合(1)的结论,得△COE≌△OBD
∴OE=BD=1.6m,OD=CE=2m
∴DE=OD-OE=0.4m
∵妈妈在距地面1.2m高的B处接住他
∴爸爸接住小明的地方,距离地面高度为:1.2+DE=1.6m.
例11.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
证明:(1)作MN⊥AD于N.
∵DM平分∠ADC,且MC⊥CD,MN⊥AD,
∴CM=MN,
∵M是BC的中点,
∴CM=MB,
∴MN=MB,
∵MB⊥BA,MN⊥AD,且MN=MB,
∴AM平分∠DAB.
角平分线的性质与判定
5
证明:(2)由(1)得MC=MN,MB=MN,
在Rt△MCD和Rt△MND中,
∴Rt△MCD≌Rt△MND (HL),
∴CD=ND,
同理可得AB=AN,
∵AD=AN+ND,
∴AD=AB+CD.
例11.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
角平分线的性质与判定
5
角平分线的性质与判定
5
例12.如图,OB平分∠MON,A为OB的中点,AE⊥ON于点E,AE=4,D为OM上一点,BC∥OM交DA的延长线于点C,则CD的最小值为______.
解析:∵BC∥OM,∴∠B=∠DOA.
∵A为OB的中点,∴AB=AO.
∵∠BAC=∠DAO,
∴△ABC≌△AOD(ASA).
∴AC=AD.
∴CD=2AD.
∴当AD有最小值时,CD有最小值.
∴当AD⊥OM时,AD有最小值.
∵OB平分∠MON,AE⊥ON,AD⊥OM,
∴AD=AE=4.
∴CD的最小值为8.
8
例13.如图,∠1=∠2,点P为BN上的一点,∠PCB+∠BAP=180°,求证:PA=PC.
B
A
C
N
)
)
1
2
P
【分析】由角平分线的性质易想到过点P向∠ABC的两边作垂线段PE、PF,构造角平分线的基本图形.
E
F
角平分线的性质与判定
5
证明:过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.
B
A
C
N
)
)
1
2
P
E
F
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足分别为E,F.
∴PE=PF, ∠PEA=∠PFC=90 °.
∵ ∠PCB+ ∠BAP=180 °,又∠BAP+∠EAP=180 °.
∴ ∠EAP=∠PCB.
在△APE和△CPF中,
∠PEA=∠PFC=90 °,
∠EAP=∠FCP,
PE=PF,
∴ △APE ≌ △CPF(AAS),
∴ AP=CP.
例13.如图,∠1=∠2,点P为BN上的一点,∠PCB+∠BAP=180 °,求证:PA=PC.
角平分线的性质与判定
5
【5-1】如图,∠1=∠2,点P为BN上的一点,PA=PC,求证:∠PCB+∠BAP=180°
B
A
C
N
)
)
1
2
P
E
F
证明:过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足分别为E,F.
∴PE=PF, ∠PEA=∠PFC=90 °.
PA=PC,
PE=PF,
在Rt△APE和Rt△CPF中,
∴ Rt△PAE ≌ Rt△PCF(HL).
∴ ∠EAP=∠FCP.
∵ ∠BAP+∠EAP=180°,
∴ ∠PCB+∠BAP=180°.
【5-2】如图,在四边形ABCD中,BC=DC,CE⊥AB于E.若∠B+∠ADC=180°,求证:AC平分∠BAD.
证明:如图,过点C作CF⊥AD,交AD的延长线于F,
∵∠B+∠ADC=180°,∠ADC+∠CDF=180°,
∴∠B=∠CDF.
在△CBE和△CDF中,
∠B=∠CDF, ∠CEB=∠CFD=90°,BC=CD,
∴△CBE≌△CDF(AAS).
∴CF=CE.
又∵CF⊥AD,CE⊥AB,
∴AC平分∠BAD.
F
【5-3】如图,∠AOB=90°,OM平分∠AOB,直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D.请判断PC与PD的数量关系并说明理由.
解:PC=PD.理由如下:
如图,过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°.
∵∠EOF=90°,∴∠FPE=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
由题意知∠CPD=90°,
∴∠1+∠FPD=90°.
又∵∠2+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE, ∠1=∠2
∴△CFP≌△DEP(ASA).
∴PC=PD.
全等三角形章节复习
1.全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;
2.掌握全等三角形的判定条件,并能进行简单的证明和计算,掌握综合法证明的格式;
3.掌握角平分线的性质及判定,能利用三角形全等证明角的平分线的性质,会利用角的平分线的性质进行证明.
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
一、全等三角形
△ABC≌△DEF
全等的表示方法:
“全等”用符号“≌”表示,读作“全等于”.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
二、全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
文字语言:三边对应相等的两个三角形全等.(简写为“边边边”或“SSS”)
基本事实---“边边边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△ A′B′C′ (SSS).
AB=A′B′,
BC=B′C′,
CA=C′A′,
几何语言:
三、三角形全等的判定方法
证明两个三角形全等的书写步骤:
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
三、三角形全等的判定方法
文字语言:两边和它们的夹角分别相等的两个三角形全等.(简写成“边角边”或“SAS”).
基本事实---“边角边”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (SAS).
AB=A′B′,
∠A=∠A′,
AC=A′C′ ,
几何语言:
三、三角形全等的判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等.(简写成“角边角”或“ASA”)
基本事实---“角边角”判定方法
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
AB=A′B′ ,
∠B=∠B′ ,
几何语言:
三、三角形全等的判定方法
◆文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等.
(可以简写成“角角边”或“AAS”).
“角角边”判定方法:
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′ (ASA).
∠A=∠A′ ,
∠B=∠B′ ,
BC=B′C′ ,
几何语言:
三、三角形全等的判定方法
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
三、三角形全等的判定方法
文字语言:角平分线上的点到角的两边的距离相等.
1.角平分线的性质
几何语言:
∵点P在∠AOB的平分线上,且PD⊥OA,PE⊥OB.
∴PD=PE
P到OA的距离
P到OB的距离
角平分线上的点
四、角平分线的性质与判定
文字语言:角的内部到角的两边的距离相等的点在角的平分线上.
2.角的平分线的判定
几何语言:
∵ PD⊥OA于D,PE⊥OB于E,PD=PE,
∴点P 在∠AOB的平分线上.(或∠1=∠2)
四、角平分线的性质与判定
角的平分线的性质
图形
已知 条件
结论
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
全等三角形的性质
1
例1.如图△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
解: ∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D,
∵∠EAB=120°,∠CAD=10°,∠B=25°,
∴∠D=∠B=25°,
∠DAE=∠BAC=(∠EAB-∠CAD)=×(120°-10°)=55°,
∴∠DFB=∠FAB+∠B=∠CAD+∠CAB+∠B
=10°+55°+25°=90°,
∴∠DGB=∠DFB-∠D=90°-25°=65°,
∴∠DFB=90°, ∠DGB=65°.
全等三角形的性质
1
例2.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D ∥EB′ ∥BC ,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
【分析】延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′,再求出∠C′+∠AHC′即可解决问题.
C
H
全等三角形的性质
1
例3.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与△ABO全等,点P与点O不重合,写出符合条件的点P的坐标:_________.
解:设点P的坐标为(a,b),
∴A(2,0) ,B(2,4)
∴OA=2,AB=4,∠OAB=90°,
由题意,分以下两种情况:
(1)如图1,当△BAP≌△ABO时,
∴PB=OA=2,∠PBA=∠OAB=90°
∴PB∥x轴,
∴b=AB=4 ,
又∵PB=2 ,
=2 ,
解得a=4或a=0,
则此时点P的坐标为P(4,4)或P(0,4) ;
全等三角形的性质
1
例3.已知点A,B的坐标分别为(2,0),(2,4),以A,B,P为顶点的三角形与△ABO全等,点P与点O不重合,写出符合条件的点P的坐标:_________.
(2)如图2,当△ABP≌△ABO时,
∴PA=OA=2, ∠PAB=∠OAB=90°
∵点P在x轴上,且OP=OA+PA=4 ,
则此时点P的坐标为P(4,0);
综上,符合条件的点P的坐标为(4,4)或(0,4)或(4,0) ,
【1-1】如图,△ABC沿BC方向平移到△DEF的位置.
(1)若∠B=30°,∠F=45°,求∠A的度数;
(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=(BF-EC)=3,
∴平移的距离BE为3.
【1-2】如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为________厘米/秒.
1或1.6
【1-3】如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A.1 B.1或4 C.1或2 D.3
B
全等三角形的判定
2
例4.如图,点P是AB上任意一点,∠ABC=∠ABD,还应补充一个条件,才能推出△APC≌△APD.从下列条件中补充一个条件,不一定能推出△APC≌△APD的是( )
A.BC=BD; B.AC=AD;
C.∠ACB=∠ADB; D.∠CAB=∠DAB
B
全等三角形的判定
2
例5.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
证明:(1)∵∠BAE=∠DAC,
∴∠BAC=∠DAE ,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS)
∴∠C=∠E.
全等三角形的判定
2
例5.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;
(2)AM=AN.
(2)∵△ABC≌△ADE
∴∠B=∠D
在△ABM和△ADN中,
∴△ABM≌△AND(ASA)
∴AM=AN.
全等三角形的判定
2
例6.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.
(1)请你找出图中其他的全等三角形;(2)试证明CF=EF.
解:(1)图中其它的全等三角形为:①△ACD≌△AEB,②△DCF≌△BEF;
②∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS).
全等三角形的判定
2
例6.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、BE.(2)试证明CF=EF.
(2)∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB,∠CAB=∠EAD,
∴∠CAB﹣∠DAB=∠EAD﹣∠DAB.
即∠CAD=∠EAB.
∴△CAD≌△EAB(SAS),
∵Rt△ABC≌Rt△ADE,△ADC≌△ABE,
∴∠ACB=∠AED,∠ACD=∠AEB,DC=BE,
∴∠DCF=∠BEF,
在△DCF和△BEF中,
∵∠CFD=∠EFB,∠DCF=∠BEF,DC=BE,
∴△CDF≌△EBF(AAS),
∴CF=EF.
【2-1】如图,已知∠B=∠DEC,AB=DE,要推得△ABC≌△DEC;
(1)若以“SAS”为依据,还缺条件______________;
(2)若以“ASA”为依据,还缺条件__________________;
(3)若以“AAS”为依据,还缺条件________________________________.
BC=EC
∠A=∠EDC
∠ACB=∠DCE (或∠ACD=∠BCE)
【2-2】如图,已知CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点0,且AO平分∠BAC,那么图中全等三角形共有______对.
4
【分析】根据条件: CD⊥AB,BE⊥AC ,AO平分∠BAC及隐含的条件AO=AO(公共边).
∴△ADO≌△AEO(AAS),∴AD=AE,
∴△ADC≌△AEB(ASA),∴∠B=∠C,
∴△ABO≌△ACO(AAS),∴BO=CO,∴△BDO≌△CEO(AAS),
∴图中全等三角形共有4对.
【2-3】如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS),
∴∠ABC=∠DEF.
①②④
③
【2-3】如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴AC=DF.
①③④
②
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
A
B
C
D
F
E
G
【分析】
欲证∠DEC=∠FEC
由平行线的性质转化为证明∠DEC=∠DCE
只需要证明△DEG≌△DCG.
全等三角形的性质与判定的综合应用
3
A
B
C
D
F
E
G
证明:∵CE⊥AD, ∴∠AGE=∠AGC=90°.
在△AGE和△AGC中,
∠AGE=∠AGC,
AG=AG,
∠EAG=∠CAG,
∴△AGE≌△AGC(ASA),
∴GE=GC.
∵AD平分∠BAC,∴∠EAG=∠CAG,.
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
全等三角形的性质与判定的综合应用
3
在△DGE和△DGC中,
EG=CG,
∠EGD=∠CGD=90°,
DG=DG.
∴△DGE≌△DGC(SAS).
∴∠DEG=∠DCG.
∵EF//BC,
∴∠FEC=∠ECD,
∴∠DEG=∠FEC.
【点睛】利用全等三角形证明角相等,首先要找到两个角所在的两个三角形,看它们全等的条件够不够;有时会用到等角转换,等角转换的途径很多,如:余角,补角的性质、平行线的性质等,必要时要想到添加辅助线.
例7.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,求证:∠DEC=∠FEC.
A
B
C
D
F
E
G
全等三角形的性质与判定的综合应用
3
全等三角形的性质与判定的综合应用
3
例8.如图,在△ADC中,DB是高,点E是DB上一点,AB=DB,EB=CB,M,N分别是AE,CD上的点,且AM=DN;
(1)试说明:△ABE △DBC;
(2)探索BM和BN的位置关系和数量关系,并说明理由.
(1)证明:∵DB是△ADC的高,∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
AB=DB,∠ABE=∠DBC,BE=BC,∴△ABE △DBC.
全等三角形的性质与判定的综合应用
3
(2)BM=BN且BM⊥BN.理由如下:∵△ABE △DBC,∴∠BAM=∠BDN.
在△ABM和△DBN中,
AB=DB,∠BAM=∠BDN,AM=DN,
∴△ABM △DBN.
∴BM=BN,∠ABM=∠DBN.
∴∠DBN+∠DBM=∠ABM+∠DBM=∠ABD=90°,即BM⊥BN.
例8.如图,在△ADC中,DB是高,点E是DB上一点,AB=DB,EB=CB,M,N分别是AE,CD上的点,且AM=DN;
(1)试说明:△ABE △DBC;
(2)探索BM和BN的位置关系和数量关系,并说明理由.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明:DE=DF:
(2)在图中,若G在AB上且∠EDG=60°,试猜想
CE,EG,BG之间的数量关系并证明所归纳结论.
(3)若题中条件“∠CAB=60°,∠CDB=120°
改为∠CAB=α,∠CDB=180°﹣α,G在AB上,
∠EDG满足什么条件时,(2)中结论仍然成立?
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明:DE=DF:
证明∵∠CAB+∠C+∠CDB+∠ABD=360°,∠CAB=60°,∠CDB=120°,
∴∠C+∠ABD=360°-60°-120°=180°,
又∵∠DBF+∠ABD=180°,
∴∠C=∠DBF,
在ΔCDE和ΔBDF中,CD=BD,∠C=∠DBF,CE=BF
∴ΔCDE ΔBDF(SAS),
∴DE=DF.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.
解:如图,连接AD,
猜想CE、EG、BG之间的数量关系为:CE+BG=EG.
证明:在ΔABD和ΔACD中AB=AC,BD=CD,AD=AD ,
∴ΔABD ΔACD(SSS),
∴∠BDA=∠CDA=∠CDB=×120°=60°,
又∵∠EDG=60°,
∴∠CDE=∠ADG,∠ADE=∠BDG,
由(1),可得ΔCDE ΔBDF,
全等三角形的性质与判定的综合应用
3
∴∠CDE=∠BDF,
∴∠BDG+∠BDF=60°,
即∠FDG=60°,
∴∠EDG=∠FDG,
在ΔDEG和ΔDFG中,DE=DF,∠EDG=∠FDG,DG=DG
∴ΔDEG ΔDFG(SAS),
∴EG=FG,
又∵CE=BF,FG=BF+BG,∴CE+BG=EG;
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.
全等三角形的性质与判定的综合应用
3
例9.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(3)若题中条件“∠CAB=60°,∠CDB=120°改为∠CAB=α,∠CDB=
180°﹣α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?
解:要使CE+BG=EG仍然成立,
则∠EDG=∠BDA=∠CDA=∠CDB,
即∠EDG= (180°-α)=90°- α,
∴当∠EDG=90°- α时,CE+BG=EG仍然成立.
【3-1】如图:在ΔABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.
(1)求证:∠ABE=∠ACG;
(2)试判:AG与AD的关系?并说明理由.
(1)证明:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠AEB=90°,
∴∠ACG+∠FAC=∠FAC+∠ABE=90°,
∴∠ABE=∠ACG;
(2)解:AG=AD,AG⊥AD,理由如下:
由(1)可知:∠ABD=∠GCA,
∵BD=AC,AB=GC,
∴△ABD≌△GCA(SAS),
∴AG=AD,∠BAD=∠CGA,
∵∠AFG=90°,
∴∠CGA+∠GAF=90°,
∴∠BAD+∠GAF=90°,即∠GAD=90°,
∴AG⊥AD.
【3-2】如图1,∠DAB=90°,CD⊥AD于点D,点E是线段AD上的一点,若DE=AB,DC=AE.
(1)判断CE与BE的关系是____________.
(2)如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD,并保持CD=AE,DE=AB,连接CB,CE,BE,试说明(1)中结论是否成立,并说明理由.
(1)解:垂直且相等,理由如下:
∵CD⊥AD,∴∠D=90°,
在△EDC与△BAE中,
ED=AB,∠D=∠DAB,DC=AE ,
∴△EDC △BAE,
∴BE=CE,∠DCE=∠AEB,
∵∠DCE+∠DEC=90°,
∴∠DEC+∠AEB=90°,即∠CEB=90°,∴CE⊥BE,∴CE与BE的关系为:垂直且相等.
【3-2】如图1,∠DAB=90°,CD⊥AD于点D,点E是线段AD上的一点,若DE=AB,DC=AE.
(1)判断CE与BE的关系是____________.
(2)如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD,并保持CD=AE,DE=AB,连接CB,CE,BE,试说明(1)中结论是否成立,并说明理由.
(2)结论成立,理由如下:
∵CD⊥AD,∴∠D=90°,
在△EDC与△BAE中,ED=AB,∠D=∠DAB,DC=AE ,∴△EDC △BAE,
∴BE=CE,∠DCE=∠AEB,
∵∠DCE+∠DEC=90°,∴∠DEC+∠AEB=90°,即∠CEB=90°,∴CE⊥BE,
∴CE与BE的关系为:垂直且相等.
【3-3】如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED,
(1)如图,若∠A+∠EDC=180°,在五边形ABCDE的外部,作△EDF≌△EAB,(不写作法,只保留作图痕迹),并说明点C,D,F三点在同一直线上;
(2)如图,若∠A=60°,∠EDC=120°,且BC=AB+CD,求证:CE平分∠BCD.
(1)解:如图作∠FED=∠AEB,EB=EF,
∵EA=ED,
∴ΔAEB ΔDEF(SAS),
∴∠A=∠EDF,
∵∠A+∠CDE=180°,
∴∠CDE+∠EDF=180°,
∴C、D、F点在同一直线上,
【3-3】如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED,
(2)如图,若∠A=60°,∠EDC=120°,且BC=AB+CD,求证:CE平分∠BCD.
(2)延长CD到T,使得DT=BA,连接ET,
∵∠CDE=120°,
∴∠EDT=180°-120°=60°,
∵∠A=60°,
∴∠A=∠EDT,
在ΔEAB和ΔEDT中,
AE=DE,∠A=∠EDT,AB=DT,
∴ΔEAB ΔEDT(SAS),
∴EB=ET,
∴CB=CD+BA=CD+DT=CT,
在ΔECB和ΔECT中,
EC=EC,EB=ET,CB=CT,
∴ΔECB ΔECT(SSS),
∴∠ECB=∠ECD,
即EC平分∠BCD.
例10.如图,小明和小华家中间隔了一个办公楼,他们想要测量自己家对面办公楼的高OM,小明在自家阳台A处测得办公楼顶部O的仰角∠1,小华在自家阳台B处测得办公楼顶部O的仰角∠2.已知C,M,D三点共线,OA⊥OB且OA=OB,AC=10m,BD=3m,CD=17m.试求办公楼的高度OM.
利用全等三角形解决实际问题
4
解:过点A作AE⊥OM,过点B作BF⊥OM,如图所示,
∵OA⊥OB,AE⊥OM,BF⊥OM,
∴∠AOB=∠AEO=∠BFO=90°,
∴∠BOF+∠2=90°,∠AOE+∠BOF=90°,
∴∠2=∠AOE,
在 AOE与 BOF中,
∠AEO=∠BFO,∠AOE=∠2,OA=OB,
∴ AOE BOF
例10.如图,小明和小华家中间隔了一个办公楼,他们想要测量自己家对面办公楼的高OM,小明在自家阳台A处测得办公楼顶部O的仰角∠1,小华在自家阳台B处测得办公楼顶部O的仰角∠2.已知C,M,D三点共线,OA⊥OB且OA=OB,AC=10m,BD=3m,CD=17m.试求办公楼的高度OM.
利用全等三角形解决实际问题
4
∴OE=BF,AE=OF,
设OM=x,则OE=OM-EM=OM-AC=x-10,
∴BF=OE=x-10,
∵OF=OM-FM=OM-BD=x-3,
∴AE=CM=CD-MD=CD-BF=17-(x-10),
17-(x-10)=x-3,
解得:x=15,
即OM=15m.
【4-1】如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的距离相等吗?
A
B
C
D
【分析】将本题中的实际问题转化为数学问题就是证明BD=CD.由已知条件可知AB=AC,AD⊥BC.
解:相等,理由如下:
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ADB和Rt△ADC中,
AD=AD,
AB=AC,
∴Rt△ADB ≌ Rt△ADC(HL).
∴BD=CD.
【4-2】如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?
解:要测量A、B间的距离,可用如下方法:
过点B作AB的垂线BF,在BF上取两点C、D,使CD=BC,
再作出BF的垂线DE,使A、C、E在一条直线上,
∵∠ACB=∠ECD,CB=CD,∠ABC=∠EDC,
∴△EDC≌△ABC(ASA).
∴DE=BA.
答:测出DE的长就是A、B之间的距离.
C
D
E
【4-3】如图是小明和爸爸妈妈在公园里荡秋千的示意图,小明坐在秋千的起始位置A处,OA与地面垂直,小明两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他.若妈妈与爸爸到OA的水平距离BD,CE分别为1.6m和2m,且∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由.
(2)爸爸是在距离地面多高的地方接住小明的?
(1)根据题意,得∠OEC=∠ODB=90°,OA=OB=OC
∴∠BOD+∠OBD=90°,∠COE+∠OCE=90°
∵∠BOC=90°
∴∠BOD+∠COE=90°
∴∠OCE=∠BOD
∴∠OEC=∠ODB,∠OCE=∠BOD,OC=OB
∴△COE≌△OBD;
【4-3】如图是小明和爸爸妈妈在公园里荡秋千的示意图,小明坐在秋千的起始位置A处,OA与地面垂直,小明两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他.若妈妈与爸爸到OA的水平距离BD,CE分别为1.6m和2m,且∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由.
(2)爸爸是在距离地面多高的地方接住小明的?
(2)结合(1)的结论,得△COE≌△OBD
∴OE=BD=1.6m,OD=CE=2m
∴DE=OD-OE=0.4m
∵妈妈在距地面1.2m高的B处接住他
∴爸爸接住小明的地方,距离地面高度为:1.2+DE=1.6m.
例11.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
证明:(1)作MN⊥AD于N.
∵DM平分∠ADC,且MC⊥CD,MN⊥AD,
∴CM=MN,
∵M是BC的中点,
∴CM=MB,
∴MN=MB,
∵MB⊥BA,MN⊥AD,且MN=MB,
∴AM平分∠DAB.
角平分线的性质与判定
5
证明:(2)由(1)得MC=MN,MB=MN,
在Rt△MCD和Rt△MND中,
∴Rt△MCD≌Rt△MND (HL),
∴CD=ND,
同理可得AB=AN,
∵AD=AN+ND,
∴AD=AB+CD.
例11.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:(1)AM平分∠DAB;(2)AD=AB+CD.
角平分线的性质与判定
5
角平分线的性质与判定
5
例12.如图,OB平分∠MON,A为OB的中点,AE⊥ON于点E,AE=4,D为OM上一点,BC∥OM交DA的延长线于点C,则CD的最小值为______.
解析:∵BC∥OM,∴∠B=∠DOA.
∵A为OB的中点,∴AB=AO.
∵∠BAC=∠DAO,
∴△ABC≌△AOD(ASA).
∴AC=AD.
∴CD=2AD.
∴当AD有最小值时,CD有最小值.
∴当AD⊥OM时,AD有最小值.
∵OB平分∠MON,AE⊥ON,AD⊥OM,
∴AD=AE=4.
∴CD的最小值为8.
8
例13.如图,∠1=∠2,点P为BN上的一点,∠PCB+∠BAP=180°,求证:PA=PC.
B
A
C
N
)
)
1
2
P
【分析】由角平分线的性质易想到过点P向∠ABC的两边作垂线段PE、PF,构造角平分线的基本图形.
E
F
角平分线的性质与判定
5
证明:过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.
B
A
C
N
)
)
1
2
P
E
F
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足分别为E,F.
∴PE=PF, ∠PEA=∠PFC=90 °.
∵ ∠PCB+ ∠BAP=180 °,又∠BAP+∠EAP=180 °.
∴ ∠EAP=∠PCB.
在△APE和△CPF中,
∠PEA=∠PFC=90 °,
∠EAP=∠FCP,
PE=PF,
∴ △APE ≌ △CPF(AAS),
∴ AP=CP.
例13.如图,∠1=∠2,点P为BN上的一点,∠PCB+∠BAP=180 °,求证:PA=PC.
角平分线的性质与判定
5
【5-1】如图,∠1=∠2,点P为BN上的一点,PA=PC,求证:∠PCB+∠BAP=180°
B
A
C
N
)
)
1
2
P
E
F
证明:过点P作PE⊥BA,PF⊥BC,垂足分别为E,F.
∵∠1=∠2,PE⊥BA,PF⊥BC,垂足分别为E,F.
∴PE=PF, ∠PEA=∠PFC=90 °.
PA=PC,
PE=PF,
在Rt△APE和Rt△CPF中,
∴ Rt△PAE ≌ Rt△PCF(HL).
∴ ∠EAP=∠FCP.
∵ ∠BAP+∠EAP=180°,
∴ ∠PCB+∠BAP=180°.
【5-2】如图,在四边形ABCD中,BC=DC,CE⊥AB于E.若∠B+∠ADC=180°,求证:AC平分∠BAD.
证明:如图,过点C作CF⊥AD,交AD的延长线于F,
∵∠B+∠ADC=180°,∠ADC+∠CDF=180°,
∴∠B=∠CDF.
在△CBE和△CDF中,
∠B=∠CDF, ∠CEB=∠CFD=90°,BC=CD,
∴△CBE≌△CDF(AAS).
∴CF=CE.
又∵CF⊥AD,CE⊥AB,
∴AC平分∠BAD.
F
【5-3】如图,∠AOB=90°,OM平分∠AOB,直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D.请判断PC与PD的数量关系并说明理由.
解:PC=PD.理由如下:
如图,过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°.
∵∠EOF=90°,∴∠FPE=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
由题意知∠CPD=90°,
∴∠1+∠FPD=90°.
又∵∠2+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE, ∠1=∠2
∴△CFP≌△DEP(ASA).
∴PC=PD.
