人教版2022-2023学年九年级数学上册 专题03 与圆有关的运动路径及面积问题 课件(共17张PPT)
文档属性
| 名称 | 人教版2022-2023学年九年级数学上册 专题03 与圆有关的运动路径及面积问题 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 10:09:05 | ||
图片预览




文档简介
(共17张PPT)
人教版九年级(上)数学教学课件
第24章 圆
专题03 与圆有关的运动路径及面积问题
情境导入
探究新知
当堂训练
典例精讲
知识归纳
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
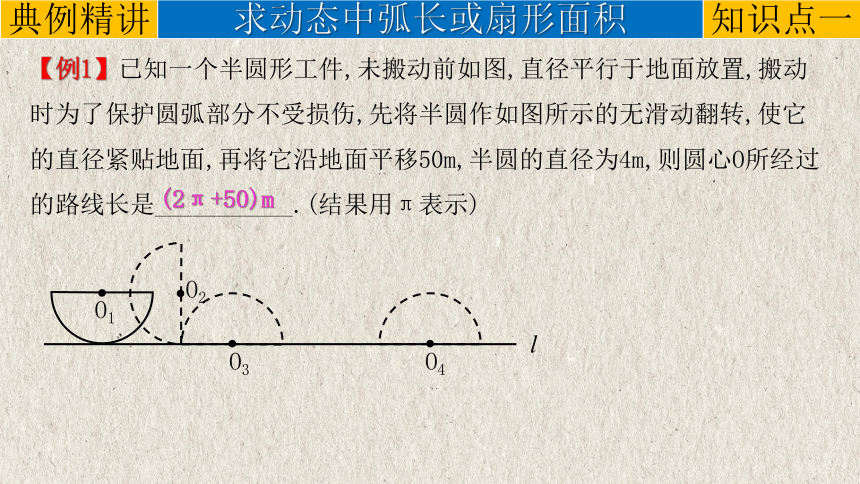
【例1】已知一个半圆形工件,未搬动前如图,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是___________.(结果用π表示)
(2π+50)m
知识点一
典例精讲
求动态中弧长或扇形面积
O1
l
O4
O3
O2
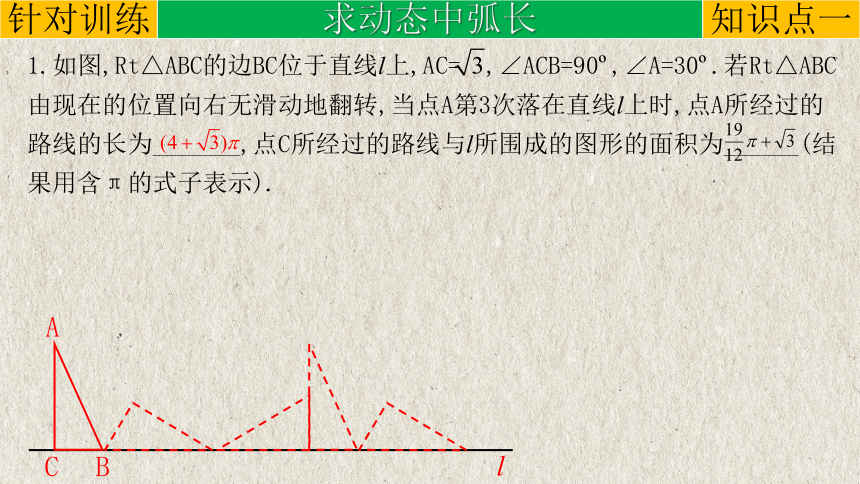
1.如图,Rt△ABC的边BC位于直线l上,AC= ,∠ACB=90 ,∠A=30 .若Rt△ABC由现在的位置向右无滑动地翻转,当点A第3次落在直线l上时,点A所经过的路线的长为_______,点C所经过的路线与l所围成的图形的面积为______(结果用含π的式子表示).
l
A
B
C
知识点一
针对训练
求动态中弧长
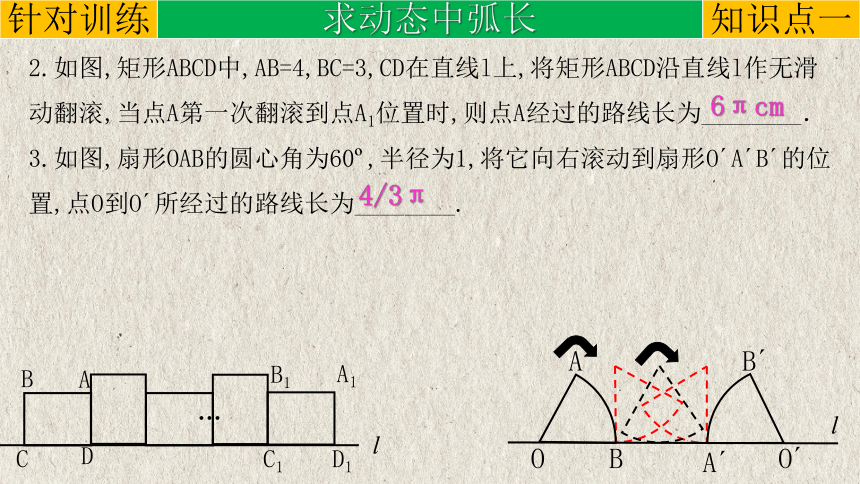
2.如图,矩形ABCD中,AB=4,BC=3,CD在直线l上,将矩形ABCD沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为________.
3.如图,扇形OAB的圆心角为60 ,半径为1,将它向右滚动到扇形O A B 的位置,点O到O 所经过的路线长为________.
6πcm
知识点一
针对训练
求动态中弧长
4/3π
A
A1
B1
…
D
C
B
l
D1
C1
O
A
A
B
B
O
l
4.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为____.
5.如图,正六边形ABCDEF是边长为2cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12cm的细线,一端固定在点A,握住另一端点P拉直细线,把它紧紧缠绕在螺母上,则点P运动的路径长为_______.
4π
14πcm
知识点一
针对训练
求动态中弧长
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
【例2】如图,一个等边三角形的边长和与它的一边相切的圆的周长相等,⊙O的半径为1cm,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动滚动,直至回到原出发位置时,则这个圆共转了___圈,点O经过的路径为____.
4
知识点二
典例精讲
折线上的滚动
O
O
A
C
B
8π
1.如图,一个正方形的边长和与它的一边相切的圆的周长相等,如果⊙P从点A的处出发,沿正方形的边无滑动地滚动,⊙P至少转___周后再次回到点A的正上方.
2.如图,⊙P的半径为r,任意四边形ABCD的周长为8πr,如果⊙P从点A的正上方出发,沿长方形的边无滑动地滚动,⊙P至少自转___周后再次回到点A的正上方.
5
知识点二
针对训练
折线上的滚动
5
P
A
D
C
B
P
A
D
C
B
3.如图,两枚1元的硬币放在桌面上,将其中一枚固定,另一枚硬币沿着固定的硬币滚动一周,回到开始的位置,则它转动的____圈.
2
知识点二
针对训练
折线上的滚动
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
【例3】如图,在矩形ABCD中,AB=4,AD= ,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,则图中阴影部分的面积_______.
(割补法)
知识点三
典例精讲
求不规则图形面积问题
A
F
D
E
C
B
O
B
A
C
D
1.如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦,AB∥CD,且与小半圆相切,AB=24.求图中阴影部分的面积.
(平移法)
H
知识点三
针对训练
求不规则图形面积问题
2.如图,在△ABC中,∠BAC=90 ,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45 至△A1B1C的位置,求线段AB扫过区域(图中阴影部分)的面积.
知识点三
针对训练
求不规则图形面积问题
B1
A
A1
C
B
(旋转法)
3.如图,在半径为1的半圆O中,C是半圆的中点,D是CB的中点则图中阴影部分的面积为___.
A
C
D
B
O
知识点三
针对训练
求不规则图形面积问题
(用等积变形法)
4.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,
EF=8,FC=10,求图中阴影部分的面积.
C
A
E
F
D
C
B
知识点三
针对训练
求不规则图形面积问题
5.如下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB,经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm,求
(1)扇形OAB的圆心角;
(2)这个纸杯的表面积.(面积计算结果保留用π).
A
B
C
D
O
E
F
6cm
4cm
8cm
S纸杯表=44π(cm2).
知识点三
针对训练
求不规则图形面积问题
人教版九年级(上)数学教学课件
第24章 圆
专题03 与圆有关的运动路径及面积问题
情境导入
探究新知
当堂训练
典例精讲
知识归纳
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
【例1】已知一个半圆形工件,未搬动前如图,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是___________.(结果用π表示)
(2π+50)m
知识点一
典例精讲
求动态中弧长或扇形面积
O1
l
O4
O3
O2
1.如图,Rt△ABC的边BC位于直线l上,AC= ,∠ACB=90 ,∠A=30 .若Rt△ABC由现在的位置向右无滑动地翻转,当点A第3次落在直线l上时,点A所经过的路线的长为_______,点C所经过的路线与l所围成的图形的面积为______(结果用含π的式子表示).
l
A
B
C
知识点一
针对训练
求动态中弧长
2.如图,矩形ABCD中,AB=4,BC=3,CD在直线l上,将矩形ABCD沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为________.
3.如图,扇形OAB的圆心角为60 ,半径为1,将它向右滚动到扇形O A B 的位置,点O到O 所经过的路线长为________.
6πcm
知识点一
针对训练
求动态中弧长
4/3π
A
A1
B1
…
D
C
B
l
D1
C1
O
A
A
B
B
O
l
4.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD,弧DE,弧EF的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长为____.
5.如图,正六边形ABCDEF是边长为2cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12cm的细线,一端固定在点A,握住另一端点P拉直细线,把它紧紧缠绕在螺母上,则点P运动的路径长为_______.
4π
14πcm
知识点一
针对训练
求动态中弧长
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
【例2】如图,一个等边三角形的边长和与它的一边相切的圆的周长相等,⊙O的半径为1cm,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动滚动,直至回到原出发位置时,则这个圆共转了___圈,点O经过的路径为____.
4
知识点二
典例精讲
折线上的滚动
O
O
A
C
B
8π
1.如图,一个正方形的边长和与它的一边相切的圆的周长相等,如果⊙P从点A的处出发,沿正方形的边无滑动地滚动,⊙P至少转___周后再次回到点A的正上方.
2.如图,⊙P的半径为r,任意四边形ABCD的周长为8πr,如果⊙P从点A的正上方出发,沿长方形的边无滑动地滚动,⊙P至少自转___周后再次回到点A的正上方.
5
知识点二
针对训练
折线上的滚动
5
P
A
D
C
B
P
A
D
C
B
3.如图,两枚1元的硬币放在桌面上,将其中一枚固定,另一枚硬币沿着固定的硬币滚动一周,回到开始的位置,则它转动的____圈.
2
知识点二
针对训练
折线上的滚动
求运动中的路径问题
01
求折线上的运动问题
02
求不规则图形面积问题
03
知识要点
精讲精练
【例3】如图,在矩形ABCD中,AB=4,AD= ,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,则图中阴影部分的面积_______.
(割补法)
知识点三
典例精讲
求不规则图形面积问题
A
F
D
E
C
B
O
B
A
C
D
1.如图是两个半圆,点O为大半圆的圆心,AB是大半圆的弦,AB∥CD,且与小半圆相切,AB=24.求图中阴影部分的面积.
(平移法)
H
知识点三
针对训练
求不规则图形面积问题
2.如图,在△ABC中,∠BAC=90 ,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45 至△A1B1C的位置,求线段AB扫过区域(图中阴影部分)的面积.
知识点三
针对训练
求不规则图形面积问题
B1
A
A1
C
B
(旋转法)
3.如图,在半径为1的半圆O中,C是半圆的中点,D是CB的中点则图中阴影部分的面积为___.
A
C
D
B
O
知识点三
针对训练
求不规则图形面积问题
(用等积变形法)
4.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,
EF=8,FC=10,求图中阴影部分的面积.
C
A
E
F
D
C
B
知识点三
针对训练
求不规则图形面积问题
5.如下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB,经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm,求
(1)扇形OAB的圆心角;
(2)这个纸杯的表面积.(面积计算结果保留用π).
A
B
C
D
O
E
F
6cm
4cm
8cm
S纸杯表=44π(cm2).
知识点三
针对训练
求不规则图形面积问题
同课章节目录
