整式的乘法3[下学期]

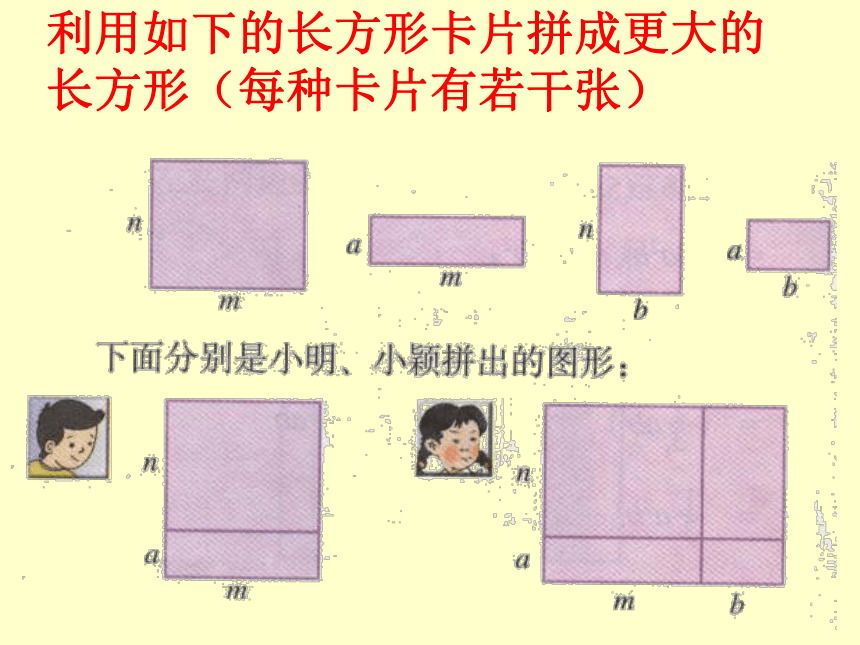
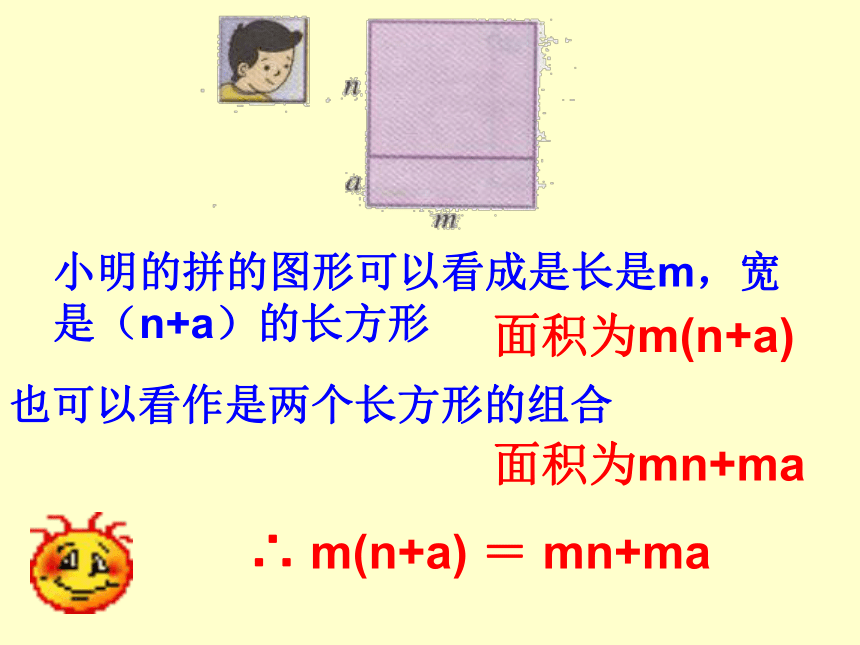
课件12张PPT。6.整式的乘法 (三)学习目标 1.经历探索多项式乘法法则的过程，理解多项式乘法法则。 2.会进行多项式乘法的运算。利用如下的长方形卡片拼成更大的长方形（每种卡片有若干张）小明的拼的图形可以看成是长是m，宽是（n+a）的长方形 面积为m(n+a) 也可以看作是两个长方形的组合 面积为mn+ma ∴ m(n+a) ＝ mn+ma 小颖拼的图形可以看作长为(m+b),宽为(n+a)的长方形 面积是(m+b)(n+a) 也可以看作是四个长方形的组合 面积是mn+ma+bn+ba. ∴ (m+b)(n+a)= mn+ma+bn+ba. 如何进行多项式相乘的运算？ 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得出的积相加。 (m+b)(n+a)=m(n+a)+ b(n+a)例1 计算（1）（1-x）(0.6-x) (2) (2x+y)(x-y)= 0.6- x- 0.6x+ x2=x -1.6x +0.62= 2x -2xy+xy-y22= 2x –xy-y22一定要用第一个多项式的每一项依次去乘第二个多项式的每一项。在计算时要注意多项式中每个单项式的符号。 注意随堂练习（1)（m+2n)(m-2n)(2) (2n+5)(n-3)(3) (x+2y)2(4) (ax+b)(cx+d)m -4n2 22n –n – 15222x + 4xy+4yacx +adx+bcx+bd2计算(a+b+c)(c+d+e)试一试=ac+ad+ae+bc+bd+be+c +cd+ce2 项数较多的两个多项式相乘，同样按法则计算。 小结 本节课你有哪些收获！用一个多项式中的每一项乘遍另一个多项式的每一项，不要漏乘。在没有合并同类项之前，两个多项式相乘展开后的项数应是这两个多项式项数之积。有同类项要合并 作业P28习题1.101、2