第23章 图形的相似自我评估试题(含答案)
文档属性
| 名称 | 第23章 图形的相似自我评估试题(含答案) | 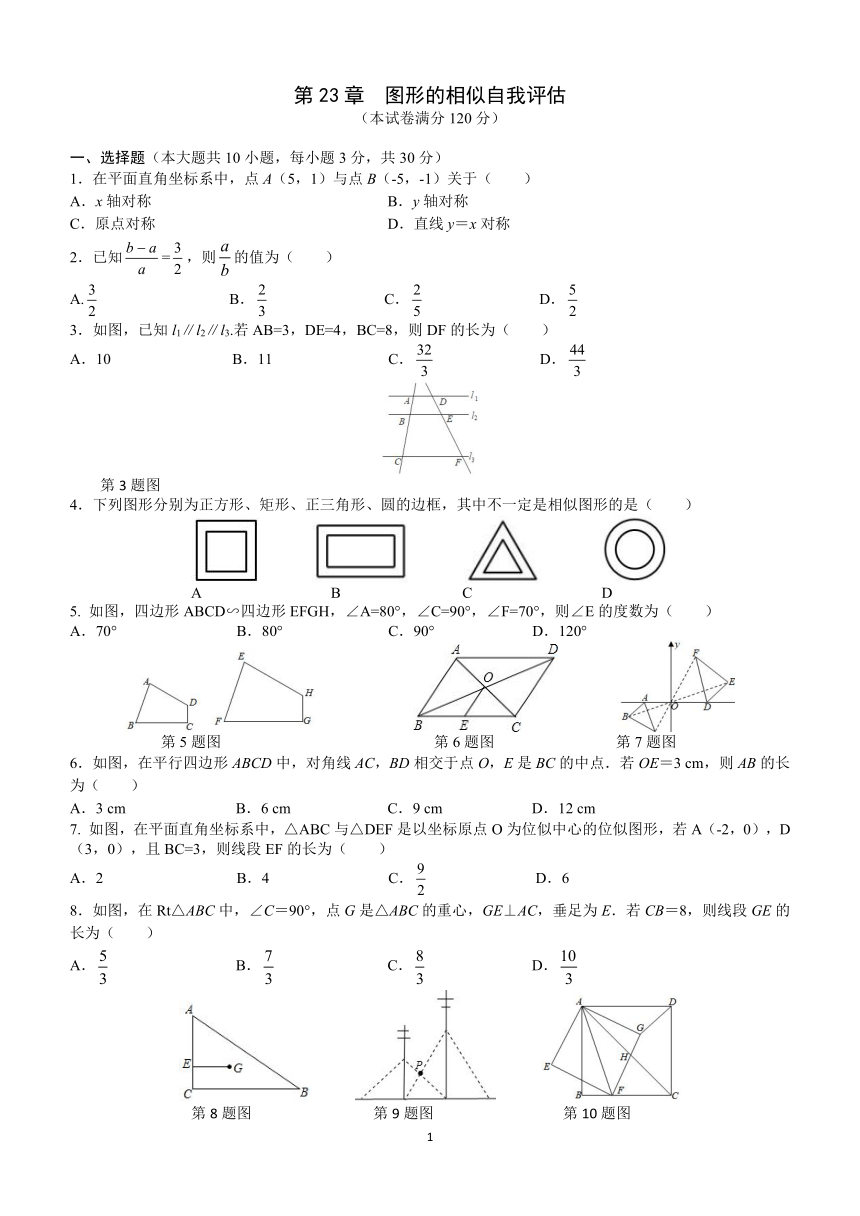 | |
| 格式 | doc | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 08:23:33 | ||
图片预览


文档简介
第23章 图形的相似自我评估
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点A(5,1)与点B(-5,-1)关于( )
A.x轴对称 B.y轴对称
C.原点对称 D.直线y=x对称
2.已知=,则的值为( )
A. B. C. D.
3.如图,已知l1∥l2∥l3.若AB=3,DE=4,BC=8,则DF的长为( )
A.10 B.11 C. D.
第3题图
4.下列图形分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A B C D
5. 如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,E是BC的中点.若OE=3 cm,则AB的长为( )
A.3 cm B.6 cm C.9 cm D.12 cm
7. 如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(-2,0),D(3,0),且BC=3,则线段EF的长为( )
A.2 B.4 C. D.6
8.如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E.若CB=8,则线段GE的长为( )
A. B. C. D.
第8题图 第9题图 第10题图
9.如图,相邻的两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,两根电线杆的钢索都各有一根固定在另一根电线杆底部,则中间两根钢索相交处点P离地面( )
A.2.4米
B.8米
C.3米
D.必须知道两根电线杆的距离才能求出点P离地面的距离
10.如图,在正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①∠EAB=∠GAD;
②△AFC∽△AGD;③2AE2=AH AC;④DG⊥AC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题4分,共24分)
11. 在比例尺为1∶36 000的某市旅游地图上,某条道路的长为7 cm,则这条道路的实际长度为 km.
12. 如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在边AB上.若只添加一个条件便能判定△ABC∽△DAE,则添加的条件是 .
第12题图 第14题图
13.在平面直角坐标系中,将点A(-2,-3)向右平移2个单位得到点B,则点B关于x轴的对称点C的坐标为 .
14.如图,在边长为6的等边三角形ABC中,AE,BD都经过△ABC的重心O.若F,G,H分别是AB,AE,BD的中点,连接FG,FH,GH,则GH的长为 .
15.有一块锐角三角形余料△ABC,已知BC的长为12.5 cm,BC边上的高为10 cm.现要把这块余料分割成若干个邻边长分别为5 cm和2 cm的小矩形零件,分割方式如图所示(分割线的耗料不计),使最底层小矩形的长为5 cm的边在BC上,则可分割成的小矩形零件最多有 个.
第15题图 第16题图
16. 如图,在平面直角坐标系中,A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A-O-B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
三、解答题(本大题共8小题,共66分)
17.(8分)已知.
(1)求的值;
(2)若x+3=(y-z)2,求x的值.
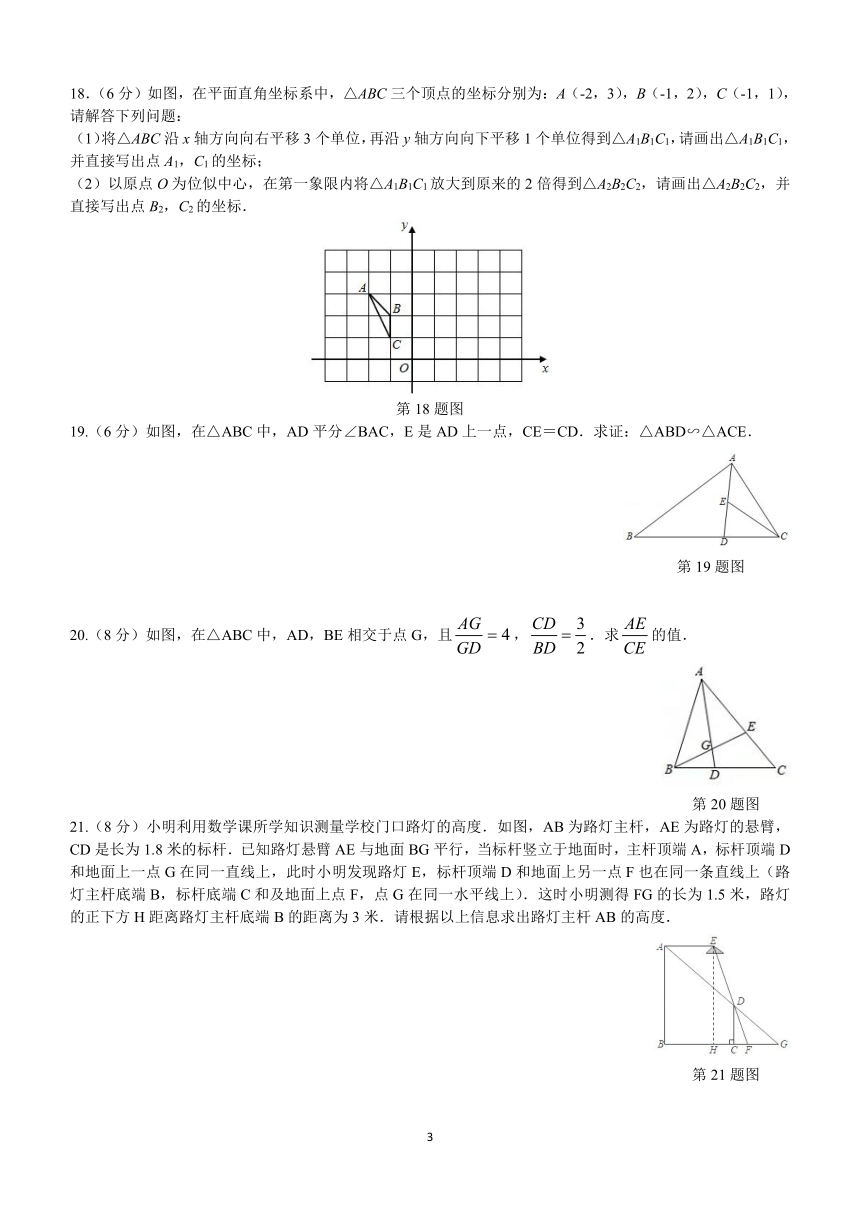
18.(6分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(-2,3),B(-1,2),C(-1,1),请解答下列问题:
(1)将△ABC沿x轴方向向右平移3个单位,再沿y轴方向向下平移1个单位得到△A1B1C1,请画出△A1B1C1,并直接写出点A1,C1的坐标;
(2)以原点O为位似中心,在第一象限内将△A1B1C1放大到原来的2倍得到△A2B2C2,请画出△A2B2C2,并直接写出点B2,C2的坐标.
第18题图
19.(6分)如图,在△ABC中,AD平分∠BAC,E是AD上一点,CE=CD.求证:△ABD∽△ACE.
第19题图
20.(8分)如图,在△ABC中,AD,BE相交于点G,且,.求的值.
第20题图
21.(8分)小明利用数学课所学知识测量学校门口路灯的高度.如图,AB为路灯主杆,AE为路灯的悬臂,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A,标杆顶端D和地面上一点G在同一直线上,此时小明发现路灯E,标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B,标杆底端C和及地面上点F,点G在同一水平线上).这时小明测得FG的长为1.5米,路灯的正下方H距离路灯主杆底端B的距离为3米.请根据以上信息求出路灯主杆AB的高度.
第21题图
22.(8分)如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M,N分别是CD,AB的中点,延长AD交NM的延长线于点E,延长BC交NM的延长线于点F.
(1)求证:∠AEN=∠F;
(2)若∠A+∠ABC=122°,求∠F的度数.
第22题图
23.(10分)如图,在△ABC中,点D,E,F分别在边AB,BC,AC上,已知DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设=,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
第23题图
24.(12分)如图,在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,连接DE,过点A作AG∥DE,分别交BD,BC于点F,G,连接FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG·BC;
(3)若AB=AC,BG=CE,连接AE,求的值.
第24题图
第23章 图形的相似自我评估参考答案
一、1. C 2. C 3. D 4. B 5. B 6. B 7. C 8. C 9. A 10. D
二、11. 2.52 12. 答案不唯一,如∠BAC=∠D 13.(0,3) 14. 15.4
16.(0,3)或(4,0)或 提示:分三种情况:①当PC∥OA时,△CPB∽△AOB,易得点P的坐标为(4,0);②当PC∥OB时,△APC∽△AOB,易得点P的坐标为(0,3);③当PC⊥AB时,△PCB∽△AOB,则,由题意可知OB=8,AB=10,BC=5,所以PB=.所以点P的坐标为.
三、17.解:设=k,则x=2k,y=3k,z=4k.
(1)==2.
(2)由题意,得2k+3=(3k-4k)2,整理,得k2-2k-3=0.
解得k=-1或k=3.
当k=-1时,x=-2;当k=3时,x=6.
所以x的值为-2或6.
18.解:(1)如图,△A1B1C1即为所求作,A1(1,2),C1(2,0).
(2)如图,△A2B2C2即为所求作,B2(4,2),C2(4,0).
第18题图
19. 证明:因为AD平分∠BAC,所以∠BAD=∠CAD.
因为CE=CD,所以∠CED=∠CDE.
因为∠CDE=∠B+∠BAD,∠CED=∠ACE+∠CAD,所以∠B=∠ACE.所以△ABD∽△ACE.
20. 解:过点D作DF∥BE,交AC于点F.
所以,.
所以AE=4EF,CF=EF.所以CE=EF.所以.
21. 解:过点D作DM⊥AB于点M,交EH于点N,则由题意可得AE∥MD∥BG.
所以∠EAD=∠FGD,∠AED=∠GFD.所以△ADE∽△GDF.
所以,即.解得AM=3.6.
所以AB=AM+BM=AM+CD=5.4(米).
答:路灯主杆AB的高度为5.4米.
22.(1)证明:因为P,M分别是BD,CD的中点,所以PM∥BC,PM=BC.
所以∠PMN=∠F.
同理,得∠PNM=∠AEN,PN=AD.
因为AD=BC,所以PN=PM.
所以∠PNM=∠PMN.
所以∠AEN=∠F.
(2)解:因为PN∥AD,所以∠PNB=∠A.
因为PM∥BC,所以∠DPM=∠DBC.
所以∠MPN=∠DPN+∠DPM=∠PNB+∠ABD+∠DBC=∠A+∠ABD+∠DBC=∠A+∠ABC=122°.
因为PM=PN,所以∠PMN=×(180°-122°)=29°.
所以∠F=∠PMN=29°.
23.(1)证明:因为DE∥AC,所以∠DEB=∠C.
因为EF∥AB,所以∠B=∠FEC.所以△BDE∽△EFC.
(2)解:①因为EF∥AB,所以==,即=.所以BE=4.
②因为=,所以=.
因为EF∥AB,所以△EFC∽△BAC.所以==.所以S△ABC=S△EFC=×20=45.
24.(1)证明:因为BD平分∠ABC,所以∠ABF=∠EBF.
因为BA=BE,BF=BF,所以△ABF≌△EBF(SAS).所以AF=EF.
同理可证得△ABD≌△EBD(SAS).所以AD=ED,∠ADB=∠EDB.
因为AG∥DE,所以∠AFD=∠EDF.所以∠AFD=∠ADF.所以AF=AD.
所以AF=EF=ED=DA.所以四边形AFED是菱形.
(2)证明:由(1),得∠BAG=∠BEF.
因为四边形AFED是菱形,所以AD∥FE.所以∠BEF=∠C.所以∠BAG=∠C.
因为∠ABG=∠CBA,所以△ABG∽△CBA.所以,即AB2=BG BC.
(3)解:因为AB=AC,所以∠ABC=∠C.
由(2)知∠BAG=∠C,所以∠BAG=∠ABC.所以AG=BG.所以∠AGC=2∠GAB.
因为BG=CE,所以BE=CG.所以CG=CA.所以∠CGA=∠CAG.
因为∠CAG=2∠DAE,所以∠DAE=∠ABC.所以∠DEA=∠ACB.所以△DAE∽△ABC.所以.
因为AB2=BG BC,AB=BE,BG=EC,所以BE2=EC BC.所以点E是BC的黄金分割点.
所以.所以.
因为∠EAC=∠C,所以CE=AE.所以=.所以=.
(3)解:因为AB=AC,所以∠ABC=∠C.
由(2)知∠BAG=∠C,所以∠BAG=∠ABC.所以AG=BG.所以∠AGC=2∠GAB.
因为BG=CE,所以BE=CG.所以CG=CA.所以∠CGA=∠CAG.
因为∠CAG=2∠DAE,所以∠DAE=∠ABC.所以∠DEA=∠ACB.所以△DAE∽△ABC.所以.
因为AB2=BG·BC,AB=BE,BG=EC,所以BE2=EC·BC,即(BC-CE)2=EC·BC.
所以.
因为∠EAC=∠C,所以CE=AE.所以=.所以=.
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点A(5,1)与点B(-5,-1)关于( )
A.x轴对称 B.y轴对称
C.原点对称 D.直线y=x对称
2.已知=,则的值为( )
A. B. C. D.
3.如图,已知l1∥l2∥l3.若AB=3,DE=4,BC=8,则DF的长为( )
A.10 B.11 C. D.
第3题图
4.下列图形分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A B C D
5. 如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,E是BC的中点.若OE=3 cm,则AB的长为( )
A.3 cm B.6 cm C.9 cm D.12 cm
7. 如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(-2,0),D(3,0),且BC=3,则线段EF的长为( )
A.2 B.4 C. D.6
8.如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E.若CB=8,则线段GE的长为( )
A. B. C. D.
第8题图 第9题图 第10题图
9.如图,相邻的两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4米处,另一根电杆钢索系在离地面6米处,两根电线杆的钢索都各有一根固定在另一根电线杆底部,则中间两根钢索相交处点P离地面( )
A.2.4米
B.8米
C.3米
D.必须知道两根电线杆的距离才能求出点P离地面的距离
10.如图,在正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①∠EAB=∠GAD;
②△AFC∽△AGD;③2AE2=AH AC;④DG⊥AC.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题4分,共24分)
11. 在比例尺为1∶36 000的某市旅游地图上,某条道路的长为7 cm,则这条道路的实际长度为 km.
12. 如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在边AB上.若只添加一个条件便能判定△ABC∽△DAE,则添加的条件是 .
第12题图 第14题图
13.在平面直角坐标系中,将点A(-2,-3)向右平移2个单位得到点B,则点B关于x轴的对称点C的坐标为 .
14.如图,在边长为6的等边三角形ABC中,AE,BD都经过△ABC的重心O.若F,G,H分别是AB,AE,BD的中点,连接FG,FH,GH,则GH的长为 .
15.有一块锐角三角形余料△ABC,已知BC的长为12.5 cm,BC边上的高为10 cm.现要把这块余料分割成若干个邻边长分别为5 cm和2 cm的小矩形零件,分割方式如图所示(分割线的耗料不计),使最底层小矩形的长为5 cm的边在BC上,则可分割成的小矩形零件最多有 个.
第15题图 第16题图
16. 如图,在平面直角坐标系中,A(0,6),B(8,0),点C是线段AB的中点,过点C的直线l将△AOB截成两部分,直线l交折线A-O-B于点P.当截成两部分中有三角形与△AOB相似时,点P的坐标为 .
三、解答题(本大题共8小题,共66分)
17.(8分)已知.
(1)求的值;
(2)若x+3=(y-z)2,求x的值.
18.(6分)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(-2,3),B(-1,2),C(-1,1),请解答下列问题:
(1)将△ABC沿x轴方向向右平移3个单位,再沿y轴方向向下平移1个单位得到△A1B1C1,请画出△A1B1C1,并直接写出点A1,C1的坐标;
(2)以原点O为位似中心,在第一象限内将△A1B1C1放大到原来的2倍得到△A2B2C2,请画出△A2B2C2,并直接写出点B2,C2的坐标.
第18题图
19.(6分)如图,在△ABC中,AD平分∠BAC,E是AD上一点,CE=CD.求证:△ABD∽△ACE.
第19题图
20.(8分)如图,在△ABC中,AD,BE相交于点G,且,.求的值.
第20题图
21.(8分)小明利用数学课所学知识测量学校门口路灯的高度.如图,AB为路灯主杆,AE为路灯的悬臂,CD是长为1.8米的标杆.已知路灯悬臂AE与地面BG平行,当标杆竖立于地面时,主杆顶端A,标杆顶端D和地面上一点G在同一直线上,此时小明发现路灯E,标杆顶端D和地面上另一点F也在同一条直线上(路灯主杆底端B,标杆底端C和及地面上点F,点G在同一水平线上).这时小明测得FG的长为1.5米,路灯的正下方H距离路灯主杆底端B的距离为3米.请根据以上信息求出路灯主杆AB的高度.
第21题图
22.(8分)如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M,N分别是CD,AB的中点,延长AD交NM的延长线于点E,延长BC交NM的延长线于点F.
(1)求证:∠AEN=∠F;
(2)若∠A+∠ABC=122°,求∠F的度数.
第22题图
23.(10分)如图,在△ABC中,点D,E,F分别在边AB,BC,AC上,已知DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设=,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
第23题图
24.(12分)如图,在△ABC中,BC>AB,BD平分∠ABC,交边AC于点D,E是BC边上一点,且BE=BA,连接DE,过点A作AG∥DE,分别交BD,BC于点F,G,连接FE.
(1)求证:四边形AFED是菱形;
(2)求证:AB2=BG·BC;
(3)若AB=AC,BG=CE,连接AE,求的值.
第24题图
第23章 图形的相似自我评估参考答案
一、1. C 2. C 3. D 4. B 5. B 6. B 7. C 8. C 9. A 10. D
二、11. 2.52 12. 答案不唯一,如∠BAC=∠D 13.(0,3) 14. 15.4
16.(0,3)或(4,0)或 提示:分三种情况:①当PC∥OA时,△CPB∽△AOB,易得点P的坐标为(4,0);②当PC∥OB时,△APC∽△AOB,易得点P的坐标为(0,3);③当PC⊥AB时,△PCB∽△AOB,则,由题意可知OB=8,AB=10,BC=5,所以PB=.所以点P的坐标为.
三、17.解:设=k,则x=2k,y=3k,z=4k.
(1)==2.
(2)由题意,得2k+3=(3k-4k)2,整理,得k2-2k-3=0.
解得k=-1或k=3.
当k=-1时,x=-2;当k=3时,x=6.
所以x的值为-2或6.
18.解:(1)如图,△A1B1C1即为所求作,A1(1,2),C1(2,0).
(2)如图,△A2B2C2即为所求作,B2(4,2),C2(4,0).
第18题图
19. 证明:因为AD平分∠BAC,所以∠BAD=∠CAD.
因为CE=CD,所以∠CED=∠CDE.
因为∠CDE=∠B+∠BAD,∠CED=∠ACE+∠CAD,所以∠B=∠ACE.所以△ABD∽△ACE.
20. 解:过点D作DF∥BE,交AC于点F.
所以,.
所以AE=4EF,CF=EF.所以CE=EF.所以.
21. 解:过点D作DM⊥AB于点M,交EH于点N,则由题意可得AE∥MD∥BG.
所以∠EAD=∠FGD,∠AED=∠GFD.所以△ADE∽△GDF.
所以,即.解得AM=3.6.
所以AB=AM+BM=AM+CD=5.4(米).
答:路灯主杆AB的高度为5.4米.
22.(1)证明:因为P,M分别是BD,CD的中点,所以PM∥BC,PM=BC.
所以∠PMN=∠F.
同理,得∠PNM=∠AEN,PN=AD.
因为AD=BC,所以PN=PM.
所以∠PNM=∠PMN.
所以∠AEN=∠F.
(2)解:因为PN∥AD,所以∠PNB=∠A.
因为PM∥BC,所以∠DPM=∠DBC.
所以∠MPN=∠DPN+∠DPM=∠PNB+∠ABD+∠DBC=∠A+∠ABD+∠DBC=∠A+∠ABC=122°.
因为PM=PN,所以∠PMN=×(180°-122°)=29°.
所以∠F=∠PMN=29°.
23.(1)证明:因为DE∥AC,所以∠DEB=∠C.
因为EF∥AB,所以∠B=∠FEC.所以△BDE∽△EFC.
(2)解:①因为EF∥AB,所以==,即=.所以BE=4.
②因为=,所以=.
因为EF∥AB,所以△EFC∽△BAC.所以==.所以S△ABC=S△EFC=×20=45.
24.(1)证明:因为BD平分∠ABC,所以∠ABF=∠EBF.
因为BA=BE,BF=BF,所以△ABF≌△EBF(SAS).所以AF=EF.
同理可证得△ABD≌△EBD(SAS).所以AD=ED,∠ADB=∠EDB.
因为AG∥DE,所以∠AFD=∠EDF.所以∠AFD=∠ADF.所以AF=AD.
所以AF=EF=ED=DA.所以四边形AFED是菱形.
(2)证明:由(1),得∠BAG=∠BEF.
因为四边形AFED是菱形,所以AD∥FE.所以∠BEF=∠C.所以∠BAG=∠C.
因为∠ABG=∠CBA,所以△ABG∽△CBA.所以,即AB2=BG BC.
(3)解:因为AB=AC,所以∠ABC=∠C.
由(2)知∠BAG=∠C,所以∠BAG=∠ABC.所以AG=BG.所以∠AGC=2∠GAB.
因为BG=CE,所以BE=CG.所以CG=CA.所以∠CGA=∠CAG.
因为∠CAG=2∠DAE,所以∠DAE=∠ABC.所以∠DEA=∠ACB.所以△DAE∽△ABC.所以.
因为AB2=BG BC,AB=BE,BG=EC,所以BE2=EC BC.所以点E是BC的黄金分割点.
所以.所以.
因为∠EAC=∠C,所以CE=AE.所以=.所以=.
(3)解:因为AB=AC,所以∠ABC=∠C.
由(2)知∠BAG=∠C,所以∠BAG=∠ABC.所以AG=BG.所以∠AGC=2∠GAB.
因为BG=CE,所以BE=CG.所以CG=CA.所以∠CGA=∠CAG.
因为∠CAG=2∠DAE,所以∠DAE=∠ABC.所以∠DEA=∠ACB.所以△DAE∽△ABC.所以.
因为AB2=BG·BC,AB=BE,BG=EC,所以BE2=EC·BC,即(BC-CE)2=EC·BC.
所以.
因为∠EAC=∠C,所以CE=AE.所以=.所以=.
