第24章 解直角三角形自我评估试题(含答案)
文档属性
| 名称 | 第24章 解直角三角形自我评估试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 423.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览



文档简介
第24章 解直角三角形自我评估
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.若sin α=,则锐角α的度数为( )
A.30° B.45° C.50° D.60°
2.在Rt△ABC中,各边都扩大3倍,则∠A的余弦值( )
A.扩大3倍 B.缩小为原来的 C.不变 D.不能确定
3.在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长为( )
A. B. C.60 D.80
4.如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cos α 米 B.4sin α 米 C.4tan α 米 D. 米
第4题图 第5题图
5.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
6.如图,在△ABC中,AB=AC,∠BAC=120°,线段AC的垂直平分线交AC于点E,交BC于点F,交BA的延长线于点D.若CF=2,则BF的长为( )
A.2 B.3 C.4 D.
第6题图 第7题图 第8题图
7.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC2的值为( )
A. B.sin2α+1 C. D.cos2α+1
8.在如图所示的方格图中,每个小正方形的边长均为1,点A,B,C,D都在格点处,AB与CD相交于点P,则sin ∠APC的值为( )
A. B. C. D.
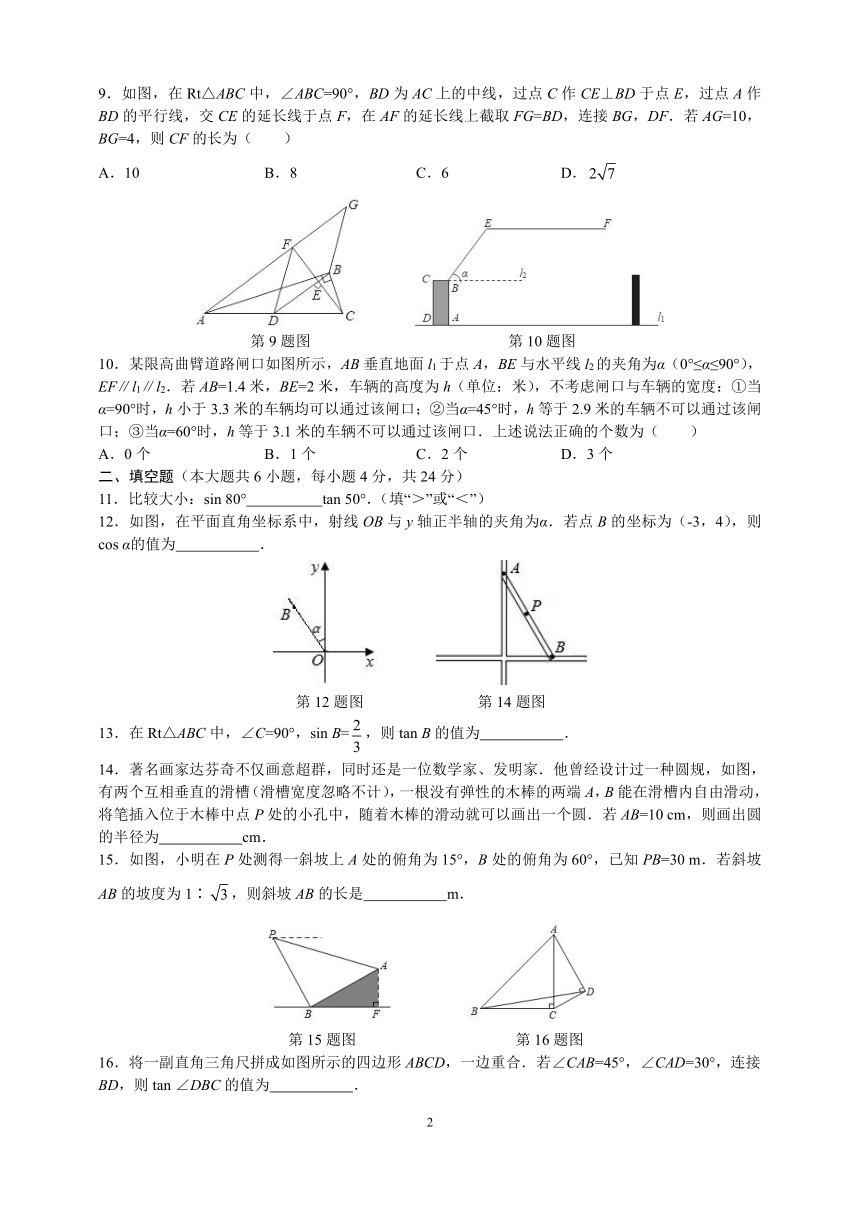
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG,DF.若AG=10,BG=4,则CF的长为( )
A.10 B.8 C.6 D.
第9题图 第10题图
10.某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2.若AB=1.4米,BE=2米,车辆的高度为h(单位:米),不考虑闸口与车辆的宽度:①当α=90°时,h小于3.3米的车辆均可以通过该闸口;②当α=45°时,h等于2.9米的车辆不可以通过该闸口;③当α=60°时,h等于3.1米的车辆不可以通过该闸口.上述说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题4分,共24分)
11.比较大小:sin 80° tan 50°.(填“>”或“<”)
12.如图,在平面直角坐标系中,射线OB与y轴正半轴的夹角为α.若点B的坐标为(-3,4),则cos α的值为 .
第12题图 第14题图
13.在Rt△ABC中,∠C=90°,sin B=,则tan B的值为 .
14.著名画家达芬奇不仅画意超群,同时还是一位数学家、发明家.他曾经设计过一种圆规,如图,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A,B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆.若AB=10 cm,则画出圆的半径为 cm.
15.如图,小明在P处测得一斜坡上A处的俯角为15°,B处的俯角为60°,已知PB=30 m.若斜坡AB的坡度为1∶,则斜坡AB的长是 m.
第15题图 第16题图
16.将一副直角三角尺拼成如图所示的四边形ABCD,一边重合.若∠CAB=45°,∠CAD=30°,连接BD,则tan ∠DBC的值为 .
三、解答题(本大题共8小题,共66分)
17.(每小题4分,共8分)计算:
(1)tan 60°-sin245°+tan 45°-2cos 30°; (2).
18.(6分)如图,在△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,E是BD的中点,连接AE.求证:BD=2AC.
第18题图
19.(6分)某游乐场新推出一个“极速飞车”项目,该项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度为i=1∶2,斜坡轨道AD的坡角∠D=36°,BC=米,CD=8米,点A,B,C,D,E均在同一平面内,求垂直升降电梯AB的高度.(精确到0.1米;参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73)
第19题图
20.(8分)如图,在△ABC中,∠B=15°,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC于点F,连接AD,AF.若AC=,求DF的长.
第20题图
21.(8分)某中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕像D处,最后从D处回到A处.已知人民英雄雕像在基地门口A处的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离.(精确到1米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
第21题图
22.(8分)如图①,图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD长为1.5 m,CD与地面DE的夹角∠CDE=15°,支架AC长为1 m,∠ACD=75°.求跑步机手柄AB所在直线与地面DE之间的距离.(精确到0.1 m;参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.73)
第22题图
23.(10分)某兴趣小组利用自制的测角仪和卷尺,测量校园国旗杆的高度,他们制定了如下两种测量方案:
方案一:第一步,在国旗杆前平地上选择一点A作为测量点,用自制的测角仪测出观察者看国旗杆顶端D的仰角α;第二步,在点A和国旗杆底端点C之间选择一点B,测出从点B看国旗杆顶端D的仰角β;第三步,测出AB两点之间的距离;第四步,计算国旗杆的高度CD.
方案二:第一步,在国旗杆前平地上选择一点A,用自制的测角仪测出观察者(竖直站立)看国旗杆顶端D的仰角α;第二步,测量观察者眼睛到地面的竖直高度AE;第三步,测量点A到国旗杆底端C的水平距离AC;第四步,在点A处重复上述操作,得到仰角及距离;第五步,计算国旗杆的高度CD.
根据以上方案,测量信息汇总如下:
课 题 测量校园国旗杆的高度
方 案 方案一 方案二
测量示意图
测量数据 项 目 α β AB的长 项 目 α AE的长 AC的长
数 据 33° 45° 5.99 m 数 据 第一次 32.7° 151.8 cm 17.47 m
第二次 33.3° 152.2 cm 17.45 m
平均值 a 152 cm b
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)请判断哪个方案更好,并说明理由;
(3)根据你的判断,选择合适的数据计算出国旗杆的高度.(精确到0.1 m;参考数据:sin 33°≈0.545,cos 33°≈0.839,tan 33°≈0.649)
24.(12分)如图,在△ABC中,∠ACB=90°,D为AB延长线上一点,连接CD,且∠DCB=∠A,
tan ∠DCB=.
(1)若BC=2,求CD的长;
(2)设BD的长为a,请用含a的代数式表示△DBC的面积.
第24题图
第24章 解直角三角形自我评估参考答案
一、1.A 2.C 3.D 4.A 5.A 6.C 7.A 8.D 9.D 10.C
二、11.< 12. 13. 14.5 15.30 16.
三、17.解:(1)原式=-+1-2×=.
(2)原式==.
18.证明:因为AD⊥AB,E是BD的中点,所以AE=BD=BE.
所以∠EAB=∠B.所以∠AEC=2∠B.
又因为∠C=2∠B,所以∠AEC=∠C.所以AE=AC.
所以BD=2AC.
19.解:由题意,得.
设BE=x米,则CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,即x2+(2x)2=()2,解得x=12.
所以BE=12,CE=24.所以DE=CD+CE=8+24=32.
在Rt△ADE中,tan D=,所以AE=DE·tan 36°≈23.36.
所以AB=AE-BE=23.36-12≈11.4(米).
答:垂直升降电梯AB的高度约为11.4米.
20.解:因为DE垂直平分AB,FG垂直平分AC,所以AD=BD,AF=CF.
所以∠DAB=∠B=15°,∠FAC=∠C=45°.
所以∠ADF=∠DAB+∠B=30°,∠AFD=∠FAC+∠C=90°.
在Rt△AFC中,sin C=,所以AF=AC·sin 45°=3.
在Rt△AFD中,tan ∠ADF=,所以DF==.
21.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
由题意,得∠CDF=37°,∠DAE=65°,AB=300,CD=200.
在Rt△CDF中,sin ∠CDF=,cos ∠CDF=,所以CF=CD·sin 37°≈120,DF=CD·cos 37°≈160.
易得四边形BEDF是矩形,所以BF=DE,BE=DF=160.所以AE=AB-BE=300-160=140.
在Rt△ADE中,tan ∠DAE=,所以DE=AE·tan 65°≈299.6.所以BF=299.6.
所以BC=BF+CF=299.6+120≈420(米).
答:革命纪念碑与党史纪念馆之间的距离约为420米.
22.解:如图,过点C作FG⊥AB于点F,交DE于点G.
因为∠CDE=15°,∠ACD=75°,所以∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+15°-75°=30°.
在Rt△AFC中,cos ∠ACF=,所以FC=AC·cos 30°=.
在Rt△CGD中,sin ∠CDE=,所以CG=CD·sin 15°≈0.39.
所以FG=FC+CG=+0.39≈1.3(m).
答:跑步机手柄AB所在直线与地面DE之间的距离约为1.3 m.
第22题图
23.解:(1)33° 17.46 m
(2)方案二更好.理由:方案一测量点A在水平地面上,不易观察,容易产生误差;方案二不仅考虑到测量点的位置,而且多次测量求其平均值,减少误差,所以方案二更好.
(3)选择方案二的数据.
过点E作EF⊥CD,垂足为F,则AE=CF=1.52,AC=EF=17.46,∠DEF=33°.
在Rt△DEF中,tan ∠DEF=,所以DF=EF·tan 33°≈17.46×0.649≈11.33(m).
所以CD=DF+FC=11.33+1.52≈12.9(m).
答:国旗杆CD的高度约为12.9 m.
24.解:(1)因为∠DCB=∠A,所以tan A=tan ∠DCB=.
在△ABC中,∠ACB=90°,tan A=,所以AC==2÷=4.所以AB==.
因为∠DCB=∠A,∠D=∠D,所以△DBC∽△DCA.所以,即.
解得BD=,CD=.
所以CD的长为.
(2)过点C作CF⊥AB于点F.
由(1)知△DBC∽△DCA,所以.
因为BD=a,所以CD=2a,AD=4a.所以AB=AD-BD=3a.
设BC=x,则AC=2x.
在Rt△ABC中,AC2+BC2=AB2,即(2x)2+x2=(3a)2,解得x=.
所以BC=,AC=.
因为CF⊥AB,所以CF==.
所以S△DBC=BD·CF=a·=.
8
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.若sin α=,则锐角α的度数为( )
A.30° B.45° C.50° D.60°
2.在Rt△ABC中,各边都扩大3倍,则∠A的余弦值( )
A.扩大3倍 B.缩小为原来的 C.不变 D.不能确定
3.在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长为( )
A. B. C.60 D.80
4.如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.4cos α 米 B.4sin α 米 C.4tan α 米 D. 米
第4题图 第5题图
5.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
6.如图,在△ABC中,AB=AC,∠BAC=120°,线段AC的垂直平分线交AC于点E,交BC于点F,交BA的延长线于点D.若CF=2,则BF的长为( )
A.2 B.3 C.4 D.
第6题图 第7题图 第8题图
7.如图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC2的值为( )
A. B.sin2α+1 C. D.cos2α+1
8.在如图所示的方格图中,每个小正方形的边长均为1,点A,B,C,D都在格点处,AB与CD相交于点P,则sin ∠APC的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ABC=90°,BD为AC上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG,DF.若AG=10,BG=4,则CF的长为( )
A.10 B.8 C.6 D.
第9题图 第10题图
10.某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2.若AB=1.4米,BE=2米,车辆的高度为h(单位:米),不考虑闸口与车辆的宽度:①当α=90°时,h小于3.3米的车辆均可以通过该闸口;②当α=45°时,h等于2.9米的车辆不可以通过该闸口;③当α=60°时,h等于3.1米的车辆不可以通过该闸口.上述说法正确的个数为( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题4分,共24分)
11.比较大小:sin 80° tan 50°.(填“>”或“<”)
12.如图,在平面直角坐标系中,射线OB与y轴正半轴的夹角为α.若点B的坐标为(-3,4),则cos α的值为 .
第12题图 第14题图
13.在Rt△ABC中,∠C=90°,sin B=,则tan B的值为 .
14.著名画家达芬奇不仅画意超群,同时还是一位数学家、发明家.他曾经设计过一种圆规,如图,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A,B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆.若AB=10 cm,则画出圆的半径为 cm.
15.如图,小明在P处测得一斜坡上A处的俯角为15°,B处的俯角为60°,已知PB=30 m.若斜坡AB的坡度为1∶,则斜坡AB的长是 m.
第15题图 第16题图
16.将一副直角三角尺拼成如图所示的四边形ABCD,一边重合.若∠CAB=45°,∠CAD=30°,连接BD,则tan ∠DBC的值为 .
三、解答题(本大题共8小题,共66分)
17.(每小题4分,共8分)计算:
(1)tan 60°-sin245°+tan 45°-2cos 30°; (2).
18.(6分)如图,在△ABC中,∠C=2∠B,D是BC上一点,且AD⊥AB,E是BD的中点,连接AE.求证:BD=2AC.
第18题图
19.(6分)某游乐场新推出一个“极速飞车”项目,该项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度为i=1∶2,斜坡轨道AD的坡角∠D=36°,BC=米,CD=8米,点A,B,C,D,E均在同一平面内,求垂直升降电梯AB的高度.(精确到0.1米;参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73)
第19题图
20.(8分)如图,在△ABC中,∠B=15°,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂直平分线交AC于点G,交BC于点F,连接AD,AF.若AC=,求DF的长.
第20题图
21.(8分)某中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕像D处,最后从D处回到A处.已知人民英雄雕像在基地门口A处的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离.(精确到1米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14)
第21题图
22.(8分)如图①,图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,踏板CD长为1.5 m,CD与地面DE的夹角∠CDE=15°,支架AC长为1 m,∠ACD=75°.求跑步机手柄AB所在直线与地面DE之间的距离.(精确到0.1 m;参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.73)
第22题图
23.(10分)某兴趣小组利用自制的测角仪和卷尺,测量校园国旗杆的高度,他们制定了如下两种测量方案:
方案一:第一步,在国旗杆前平地上选择一点A作为测量点,用自制的测角仪测出观察者看国旗杆顶端D的仰角α;第二步,在点A和国旗杆底端点C之间选择一点B,测出从点B看国旗杆顶端D的仰角β;第三步,测出AB两点之间的距离;第四步,计算国旗杆的高度CD.
方案二:第一步,在国旗杆前平地上选择一点A,用自制的测角仪测出观察者(竖直站立)看国旗杆顶端D的仰角α;第二步,测量观察者眼睛到地面的竖直高度AE;第三步,测量点A到国旗杆底端C的水平距离AC;第四步,在点A处重复上述操作,得到仰角及距离;第五步,计算国旗杆的高度CD.
根据以上方案,测量信息汇总如下:
课 题 测量校园国旗杆的高度
方 案 方案一 方案二
测量示意图
测量数据 项 目 α β AB的长 项 目 α AE的长 AC的长
数 据 33° 45° 5.99 m 数 据 第一次 32.7° 151.8 cm 17.47 m
第二次 33.3° 152.2 cm 17.45 m
平均值 a 152 cm b
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)请判断哪个方案更好,并说明理由;
(3)根据你的判断,选择合适的数据计算出国旗杆的高度.(精确到0.1 m;参考数据:sin 33°≈0.545,cos 33°≈0.839,tan 33°≈0.649)
24.(12分)如图,在△ABC中,∠ACB=90°,D为AB延长线上一点,连接CD,且∠DCB=∠A,
tan ∠DCB=.
(1)若BC=2,求CD的长;
(2)设BD的长为a,请用含a的代数式表示△DBC的面积.
第24题图
第24章 解直角三角形自我评估参考答案
一、1.A 2.C 3.D 4.A 5.A 6.C 7.A 8.D 9.D 10.C
二、11.< 12. 13. 14.5 15.30 16.
三、17.解:(1)原式=-+1-2×=.
(2)原式==.
18.证明:因为AD⊥AB,E是BD的中点,所以AE=BD=BE.
所以∠EAB=∠B.所以∠AEC=2∠B.
又因为∠C=2∠B,所以∠AEC=∠C.所以AE=AC.
所以BD=2AC.
19.解:由题意,得.
设BE=x米,则CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,即x2+(2x)2=()2,解得x=12.
所以BE=12,CE=24.所以DE=CD+CE=8+24=32.
在Rt△ADE中,tan D=,所以AE=DE·tan 36°≈23.36.
所以AB=AE-BE=23.36-12≈11.4(米).
答:垂直升降电梯AB的高度约为11.4米.
20.解:因为DE垂直平分AB,FG垂直平分AC,所以AD=BD,AF=CF.
所以∠DAB=∠B=15°,∠FAC=∠C=45°.
所以∠ADF=∠DAB+∠B=30°,∠AFD=∠FAC+∠C=90°.
在Rt△AFC中,sin C=,所以AF=AC·sin 45°=3.
在Rt△AFD中,tan ∠ADF=,所以DF==.
21.解:过点D作DE⊥AB于点E,DF⊥BC于点F.
由题意,得∠CDF=37°,∠DAE=65°,AB=300,CD=200.
在Rt△CDF中,sin ∠CDF=,cos ∠CDF=,所以CF=CD·sin 37°≈120,DF=CD·cos 37°≈160.
易得四边形BEDF是矩形,所以BF=DE,BE=DF=160.所以AE=AB-BE=300-160=140.
在Rt△ADE中,tan ∠DAE=,所以DE=AE·tan 65°≈299.6.所以BF=299.6.
所以BC=BF+CF=299.6+120≈420(米).
答:革命纪念碑与党史纪念馆之间的距离约为420米.
22.解:如图,过点C作FG⊥AB于点F,交DE于点G.
因为∠CDE=15°,∠ACD=75°,所以∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+15°-75°=30°.
在Rt△AFC中,cos ∠ACF=,所以FC=AC·cos 30°=.
在Rt△CGD中,sin ∠CDE=,所以CG=CD·sin 15°≈0.39.
所以FG=FC+CG=+0.39≈1.3(m).
答:跑步机手柄AB所在直线与地面DE之间的距离约为1.3 m.
第22题图
23.解:(1)33° 17.46 m
(2)方案二更好.理由:方案一测量点A在水平地面上,不易观察,容易产生误差;方案二不仅考虑到测量点的位置,而且多次测量求其平均值,减少误差,所以方案二更好.
(3)选择方案二的数据.
过点E作EF⊥CD,垂足为F,则AE=CF=1.52,AC=EF=17.46,∠DEF=33°.
在Rt△DEF中,tan ∠DEF=,所以DF=EF·tan 33°≈17.46×0.649≈11.33(m).
所以CD=DF+FC=11.33+1.52≈12.9(m).
答:国旗杆CD的高度约为12.9 m.
24.解:(1)因为∠DCB=∠A,所以tan A=tan ∠DCB=.
在△ABC中,∠ACB=90°,tan A=,所以AC==2÷=4.所以AB==.
因为∠DCB=∠A,∠D=∠D,所以△DBC∽△DCA.所以,即.
解得BD=,CD=.
所以CD的长为.
(2)过点C作CF⊥AB于点F.
由(1)知△DBC∽△DCA,所以.
因为BD=a,所以CD=2a,AD=4a.所以AB=AD-BD=3a.
设BC=x,则AC=2x.
在Rt△ABC中,AC2+BC2=AB2,即(2x)2+x2=(3a)2,解得x=.
所以BC=,AC=.
因为CF⊥AB,所以CF==.
所以S△DBC=BD·CF=a·=.
8
