浙教版科学2022-2023学年上学期九年级“冲刺重高”讲义(二十九):杠杆的动态平衡及应用【word,含答案】
文档属性
| 名称 | 浙教版科学2022-2023学年上学期九年级“冲刺重高”讲义(二十九):杠杆的动态平衡及应用【word,含答案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览




文档简介
一、最大动力臂和最小动力
由F1 × L1=F2 × L2知,当阻力、阻力臂一定时,动力臂越长,动力越小,动力臂最长时,动力最小。要求最小动力,应先求最大动力臂。
(1)找最大动力臂的方法:
①动力作用点确定时,支点到动力作用点的线段长即为最大动力臂;
②动力作用点没有确定时,应看杠杆上哪一点离支点最远,则这一点到支点的线段长即为最大动力臂。
(2)最小动力的作法:
①作出最大动力臂(即连接支点与最远点作为最大动力臂);
②过动力作用点作最大动力臂的垂线,根据实际情况确定动力方向。
(3)若动力臂和阻力一定时,由杠杆平衡条件可知,阻力臂最小时,动力最小。
二、杠杆的动态平衡问题
先找出杠杆的相关要素——支点、动力、动力臂、阻力、阻力臂,当杠杆水平时,如果动力臂最长,也就是说动力是最小的。因此,根据杠杆的平衡条件可继续分析出,当力的方向改变时,对力臂与力的影响。
【能力拓展】明确力的方向是竖直还是垂直方向非常重要,再根据公式解题。
我国古代人们对杠杆的应用
早在 3000 多年以前,勤劳智慧的中国人就已经开始使用杠杆。他们发明了用来捣谷的舂,用来在井上汲水的桔槔,以及用来精确测量质量的天平和杆秤等。
在公元前 4~ 公元前 3世 纪 写 成 的《墨 经》中就对天平的平衡原理作了精辟的论述:“衡木:加重于其一旁,必捶一重相若也。”意思是:天平横梁的一臂加重物,另一臂也要加砝码,两者必须等重,才能平衡。
例1、如图,圆柱形物体重力为G、横截面积是半径为R的圆,要从高度为0.5R的台面上滚过去,请画出最省力的作用点和力方向________;此时力F和G的关系是:________。
例2、如图所示,O为杠杆的支点,为了提高重物P,用一个跟杠杆保持垂直的力使杠杆由竖直位置转动到水平位置,在这个过程中( )
A.杠杆始终是省力的 B.杠杆始终是费力的
C.先是省力的,后是费力的 D.先是费力的,后是省力的
例3、如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10N的重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆________(选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是________(选填“变大”、“变小”、“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示,请在答题卷上画出动力F丙随时间t的变化趋势________。
例4、做好垃圾分类是每个公民应尽的责任和义务。
(1)下列垃圾属于有害垃圾的是 ,
A.废电池 B.碎玻璃 C.枯枝败叶 D.过期药品
(2)如图甲所示是脚踏式翻盖垃圾桶的实物图,翻盖的原理利用了杠杆,图乙所示是两个杠杆组合的示意图。桶盖的质量为800g,脚踏杆和其他连接杆的质量不计,已知O 1 A=30cm,AB=51cm,CO 2=5cm,桶盖DO2质量分布均匀,厚度不计,D为重心,桶盖闭合时,连接杆BC处于竖直状态。
①由图乙可知,DCO2为________(选填“省力”或“费力”)杠杆;
②若要把桶盖翻开,脚对踏板 A处的压力至少为________。
1.如图所示,杠杆始终处于水平平衡状态,改变弹簧测力计拉力的方向,使其从位置①到位置②,再到位置③。此过程中,弹簧测力计的示数将( ) 。
A.逐渐变大 B.逐渐变小 C.先变大后变小 D.先变小后变大
2.指甲刀是生活中常用的小工具,如图所示,它包含三个杠杆,关于这三个杠杆的说法正确的是( )
A.一个省力杠杆,两个费力杠杆 B.一个费力杠杆,两个省力杠杆
C.三个都是省力杠杆 D.三个都是费力杠杆
3.衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是( )
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
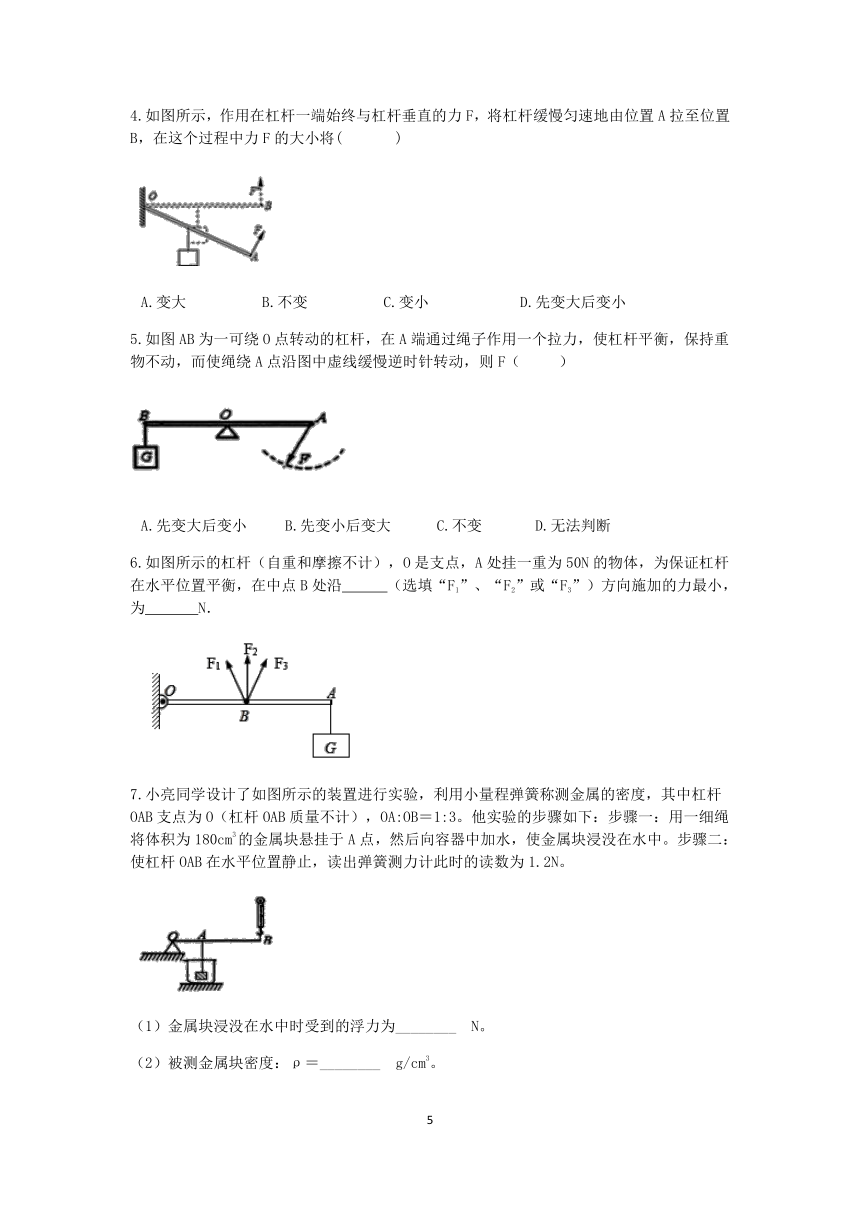
4.如图所示,作用在杠杆一端始终与杠杆垂直的力F,将杠杆缓慢匀速地由位置A拉至位置B,在这个过程中力F的大小将( )
A.变大 B.不变 C.变小 D.先变大后变小
5.如图AB为一可绕O点转动的杠杆,在A端通过绳子作用一个拉力,使杠杆平衡,保持重物不动,而使绳绕A点沿图中虚线缓慢逆时针转动,则F( )
A.先变大后变小 B.先变小后变大 C.不变 D.无法判断
6.如图所示的杠杆(自重和摩擦不计),O是支点,A处挂一重为50N的物体,为保证杠杆在水平位置平衡,在中点B处沿 (选填“F1”、“F2”或“F3”)方向施加的力最小,为 N.
7.小亮同学设计了如图所示的装置进行实验,利用小量程弹簧称测金属的密度,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________ N。
(2)被测金属块密度:ρ=________ g/cm3。
1.如图所示的杠杆AB处于平衡状态,O点为杠杆的支点,则力F力臂是( )
A.OF B.OD
C.OC D.DF
2.有一根一端粗一端细的木棒,用绳子拴住木棒的O点,将它悬挂起来,恰好处于水平位置平衡,如图所示,若把木棒从绳子悬挂处锯开,则被锯开的木棒( )
A.粗细两端一样重 B.粗端较重 C.细端较重 D.无法判定
3.如图所示,轻质杠杆0A中点悬挂一重为60牛的物体C,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是 。保持F的方向不变,将杠杆从A位置匀速提升到B位置,该过程中力F将 。
4.杆秤是一种用来测量物体质量的工具。小金尝试做了如图所示的杆秤。在秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,于是小金将此处标为0刻度。当秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡测得OA=5cm,OB=10cm。
(1)计算秤砣的质量m砣 =________ kg
(2)小金在B处标的刻度应为________kg。若图中OC=2OB,则C处的刻度应为________Kg
(3)当秤盘上放一个质量为2kg的物体时,若换用一个质量更大的秤砣,移动秤砣使杆秤再次水平平衡时,其读数________(选填“<”或“>”)2kg,由此可知一杆杄秤不能随意更换秤砣 。
5.将酒敞口放置,酒精度(酒中酒精的体积百分比)会变化吗?小科认为:只要确定酒的密度是否变化就能作出判断。于是利用身边的物品,动手制作“密度秤”来测量酒的密度。
步骤Ⅰ:按图甲制作好秤杆,提起提纽,移动秤砣(小螺母),当秤杆水平平衡时用笔将此时秤砣的悬挂点B标记为“0”刻度(单位:g/cm3)。
步骤Ⅱ:按图乙所示,将大螺母浸没在水中(大螺母必须浸没且不碰底),提起提纽,移动秤砣,当秤杆水平平衡时用笔将此时秤砣的悬挂点C标记为“1”刻度。再将BC两刻度之间分为10等份。
步骤Ⅲ:测量酒的密度。
(1).应用:小科,用该密度秤分别测出瓶盖刚打开和敞口一段时间后酒的密度约为0.92g/cm3和0.96g/cm3 ,已知酒精密度为0.8g/cm3 , 应用密度知识可判断出其酒精度 (填“变大”“不变”或“变小")。
(2).反思:在制作和测量过程中,大螺母必须浸没的目的是 。
(3).拓展:小科若要测量食盐水的密度,他应先在密度秤上增加大于1的刻度,请你写出利用直尺和笔标定刻度的过程: 。
答案及解析
例1、【答案】 ;F<G
【解析】在杠杆上,当以支点到作用点之间的线段为动力臂时最长,这时动力最小,因此找到圆周上到支点距离最远的点即可。
【解答】在圆周上,两点之间最长的就是直径。从支点做通过支点的直径,与圆周的交点就是力的作用点,然后通过它做这条直径的垂线即可。
由杠杆平衡条件,F1L1=F2L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;元的直径作为最长力臂,由图知,动力的方向应该向上,作用点在圆的切线位置,如图,比较可知,L1>L2 , 所以F<G
例2、【答案】C
【解析】分析杠杆旋转的过程中,动力臂和阻力臂的大小关系,根据杠杆的平衡条件判断即可。
【解答】在杠杆由竖直位置转动到水平位置时,动力臂L1的长度始终不变。在开始的一端时间内,动力臂L1>L2,为省力杠杆;后来,动力臂L1<L2,为费力杠杆,因此这个杠杆先是省力的,后是费力的。
故选C。
例3、【答案】不一定;变小;
【解析】(1)阻力臂为,动力F甲的方向不确定,那么动力臂的长度可能大于,也可能小于,所以该杠杆不一定是省力杠杆;
(2)在杠杆由水平位置匀速向上提升重物的过程中,阻力G保持不变,但是阻力臂L2不断减小,动力臂L1=OA保持不变;根据杠杆的平衡条件G×L2=F乙×OA可知,动力F乙逐渐变小;
(3)如下图所示:
若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向, 当动力臂为OB时最长,即动力臂先变大后变小。根据杠杆的平衡条件G×L2=F丙×L1可知,G和L2保持不变,那么动力F丙的变化应该是先变小后变大。如下图所示:
例4、【答案】(1)A,D (2)费力;39.2N
【解析】(1)垃圾的分类有可回收垃圾、其它垃圾(干垃圾)、厨余垃圾(湿垃圾)、有害垃圾;
①可回收物主要包括废纸、塑料、玻璃、金属和布料五大类;
②其他垃圾包括除上述几类垃圾之外的砖瓦陶瓷、渣土、卫生间废纸、纸巾等难以回收的废弃物及果壳、尘土、食品袋(盒);
③厨余垃圾包括剩菜剩饭、骨头、菜根菜叶、果皮等食品类废物,
④有害垃圾含有对人体健康有害的重金属、有毒的物质或者对环境造成现实危害或者潜在危害的废弃物。
(2)①比较动力臂和阻力臂的大小,从而确定杠杆的分类;
②在杠杆DCO2上,根据杠杆的平衡条件F1L1=F2L2计算出作用在顶杆BC上的力;在杠杆AB上,再次利用杠杆的平衡条件计算出作用在A处的压力。
【解答】(1)废电池和过期药品属于有害垃圾,碎玻璃和枯枝败叶属于其它垃圾,故选AD。
(2)①对于杠杆DCO2来说,桶盖的重力相当于阻力,阻力臂为DO2;顶杆BC对桶盖的支持力为动力,动力臂为CO2,此时动力臂小于阻力臂,为费力杠杆。
②对于杠杆DCO2来说,据杠杆的平衡条件F1L1=F2L2得到:G×DO2=FCB×CO2;
0.8kg×10N/kg×(30cm+5cm)=FCB×5cm;
解得:FCB=56N;
在杠杆AB上,据杠杆的平衡条件F1L1=F2L2得到:F×AO1=FCB×BO1;
F×30cm=56N×(51cm-30cm);
解得:F=39.2N。
1.【解析】根据杠杆的平衡条件F1L1=F2L2分析。
【解答】根据杠杆的平衡条件F1L1=F2L2可知,当阻力和阻力臂保持不变时,动力与动力臂的长度成反比。根据图片可知,当测力计的拉力方向从①到③时,动力臂先变大后变小,则弹簧测力计的示数先变小后变大,故D正确,而A、B、C错误。
故选D。
2.【答案】A
【解析】根据动力臂和阻力臂的大小关系确定杠杆的种类。
①对于杠杆CBA来说,C点为支点,阻力作用在B点,动力作用在A点,此时动力臂大于阻力臂,为省力杠杆;
②对于杠杆DBO来说,支点为O,动力作用在B点,阻力作用在D点,此时动力臂小于阻力臂,为费力杠杆;
③对于杠杆DEO来说,O为支点,动力作用在E点,阻力作用在D点,此时动力臂小于阻力臂,为费力杠杆。
因此指甲刀包括一个省力杠杆,两个费力杠杆。故选A。
3.【答案】B
【解析】如果动力臂大于阻力臂,那么为省力杠杆;如果动力臂小于阻力臂,那么为费力杠杆。
夹子的轴是杠杆的支点O;
(1)当用手将其捏开时,弹簧的压力为阻力,手的压力为动力,此时动力臂大于阻力臂,为省力杠杆;
(2)当用其夹住物品时,弹簧的压力为动力,而夹口上的物体施加阻力,此时动力臂小于阻力臂,为费力杠杆。故B正确,而A、C、D错误。故选B。
4.【答案】A
【解析】注意分析杠杆改变位置的过程中,动力臂和阻力臂的变化,然后根据杠杆的平衡条件分析动力F的变化即可。
根据图片可知,物体的重力为阻力,拉力F为动力;
根据杠杆的平衡条件得到:G×L2=F×L1;
由于拉力F始终与杠杆垂直,所以动力臂L1保持不变;
在杠杆旋转的过程中,阻力臂L2逐渐增大,那么G×L2=F×L1中的乘积变大;因为L1不变,所以动力F不断增大,故A正确,而B、C、D错误。
5.【答案】B
【解析】在杠杆上,从支点到力的作用点为力臂时最长,此时动力最小;分析拉力在转动过程中动力臂的长度变化即可。
【解答】分析可知,当力F与杠杆AB垂直时,此时动力臂最长,因此在力F转动的过程中,动力臂先变长后变短;根据杠杆的平衡条件可知,力F先变小后变大。故选B。
6.【答案】:F2;100。
【解析】为使拉力最小,动力臂要最长,拉力F的方向应该垂直杠杆向上,即竖直向上(F2),动力臂为OB最长,
杠杆在水平位置平衡,根据杠杆的平衡条件:
F2×OB=G×OA,由于OA是OB的二倍,所以:F=2G=100N。
7.【答案】(1)1.8(2)3
【解析】(1)由公式:,
;
(2)由于杠杆平衡可得:
对金属块进行受力分析可知,金属受向下的重力,向上的浮力F浮和绳子对金属块向上的拉力(与F1是一对相互作用力),三力作用下金属块处于平衡状态。
,
1.【答案】C
【解析】已知O为支点,力臂是从支点O到力的作用线的距离,故左端拉力F的力臂是OC;
2.【答案】B
【解析】将悬挂点O看做支点,左边木棒的重力为阻力,右边木棒的重力为动力。根据图片可知,左端的阻力臂肯定小于右端的动力臂,根据杠杆平衡条件F1L1=F2L2可知,左端木棒的重力肯定大于右端木棒的重力,故B正确,而A、C、D错误。故选B。
3.【解析】(1)根据杠杆的平衡条件F1L1=F2L2计算。
(2)注意分析动力臂和阻力臂的比值是否发生改变即可。
【解答】(1)根据图片可知,O为支点,G为阻力,阻力臂为;F为动力,动力臂为OA。根据杠杆的平衡条件F1L1=F2L2得到:F×OA=60N×;
解得:F=30N。
(2)原来杠杆在水平位置平衡时,根据杠杆的平衡条件得到: ①;
在杠杆提升的过程中,如下图所示:
△OCC'与△OAA'相似,则 ②;
根据杠杆的平衡条件得到: ③;
①②③联立得到:F=F';
则该过程中F大小不变。
4.【解析】(1)秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡,根据杠杆平衡条件F1L1=F2L2计算秤砣的质量;
(2)秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,由此知O处为0刻度,由此知B处标的刻度值,然后根据杠杆的平衡条件F1L1=F2L2计算出C处的刻度值。
(3)根据杠杆的平衡条件F1L1=F2L2分析判断。
【解答】(1)由杠杆的平衡条件F1L1=F2L2得到:
m物g×AO=m砣g×OB; m物×AO=m砣×OB; 2kg×5cm=m砣×10cm;
解得:m砣=1kg;
(2)秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,由此知O处为0刻度,
秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡,所以在B处标的刻度应为2kg;
秤砣在C处时杆秤恰好水平平衡,此时秤盘上放的重物质量为m,
则mg×AO=m砣g×OC;
所以m×AO=m砣×2OB;
m×5cm=1kg×2×10cm;
解得:m=4kg,
所以C处刻度应为4kg。
(3)由杠杆的平衡条件可知:G物×OA=G砣×l,G物×OA的值不变,G砣增大,力臂l变小,读数变小,故读数小于2kg。
5.【解析】(1)白酒其实是酒精和水的混合液,因为水的密度大于酒精的密度,所以水越多,白酒的密度越大;酒精越多,白酒的密度越小;
(2)大螺母受到浮力的大小直接影响所测液体的密度,而浮力受到液体密度和排开液体体积的影响,根据控制变量法的要求可知,探究浮力的大小与液体密度的关系时,必须控制排开液体的体积相同;
(3)根据图片可知,液体的密度越大,刻度值越靠左,且液体的密度与刻度值成正比。B点为0,C点为1,可以根据BC的长度在C点左侧量取得到D点,这就是刻度2的位置,将CD之间平均分成10份每份就是0.1,据此刻度标注完成。也可以将CB之间平均分成10份,得到0.1的长度,据此在C点左侧依次画出对应的刻度值即可。
【解答】(1)敞口一段时间后,白酒溶液的密度增大了,说明其中的酒精减小,而水相对增多了,故酒精度变小。
(2)反思:在制作和测量过程中,大螺母必须浸没的目的是:控制排开的液体体积相同。
(3)利用直尺和笔标定刻度的过程:
方法一:先测出BC的长度,以C点为起点向左画出与BC等长的CD,再把CD长度十等分;
方法二:先测每小格的长度,以C点为起点向左画出与前面每小格等距的刻度。
2022-2023学年上学期浙教版科学九年级“冲刺重高”讲义(二十九)
杠杆的动态平衡及应用
由F1 × L1=F2 × L2知,当阻力、阻力臂一定时,动力臂越长,动力越小,动力臂最长时,动力最小。要求最小动力,应先求最大动力臂。
(1)找最大动力臂的方法:
①动力作用点确定时,支点到动力作用点的线段长即为最大动力臂;
②动力作用点没有确定时,应看杠杆上哪一点离支点最远,则这一点到支点的线段长即为最大动力臂。
(2)最小动力的作法:
①作出最大动力臂(即连接支点与最远点作为最大动力臂);
②过动力作用点作最大动力臂的垂线,根据实际情况确定动力方向。
(3)若动力臂和阻力一定时,由杠杆平衡条件可知,阻力臂最小时,动力最小。
二、杠杆的动态平衡问题
先找出杠杆的相关要素——支点、动力、动力臂、阻力、阻力臂,当杠杆水平时,如果动力臂最长,也就是说动力是最小的。因此,根据杠杆的平衡条件可继续分析出,当力的方向改变时,对力臂与力的影响。
【能力拓展】明确力的方向是竖直还是垂直方向非常重要,再根据公式解题。
我国古代人们对杠杆的应用
早在 3000 多年以前,勤劳智慧的中国人就已经开始使用杠杆。他们发明了用来捣谷的舂,用来在井上汲水的桔槔,以及用来精确测量质量的天平和杆秤等。
在公元前 4~ 公元前 3世 纪 写 成 的《墨 经》中就对天平的平衡原理作了精辟的论述:“衡木:加重于其一旁,必捶一重相若也。”意思是:天平横梁的一臂加重物,另一臂也要加砝码,两者必须等重,才能平衡。
例1、如图,圆柱形物体重力为G、横截面积是半径为R的圆,要从高度为0.5R的台面上滚过去,请画出最省力的作用点和力方向________;此时力F和G的关系是:________。
例2、如图所示,O为杠杆的支点,为了提高重物P,用一个跟杠杆保持垂直的力使杠杆由竖直位置转动到水平位置,在这个过程中( )
A.杠杆始终是省力的 B.杠杆始终是费力的
C.先是省力的,后是费力的 D.先是费力的,后是省力的
例3、如图所示,OAB是杠杆,OA与BA垂直,在OA的中点处挂一个G=10N的重物,杠杆重力及摩擦均不计。若加在B点的动力F甲使OA在水平位置保持静止,如图甲所示,那么,该杠杆________(选填“一定”或“不一定”)是省力杠杆;若动力F乙始终与OA垂直,将杠杆由水平位置匀速向上提升重物,如图乙所示,动力F乙的大小变化是________(选填“变大”、“变小”、“先变大后变小”或“先变小后变大”);若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向,在此过程中OA始终保持水平静止,如图丙所示,请在答题卷上画出动力F丙随时间t的变化趋势________。
例4、做好垃圾分类是每个公民应尽的责任和义务。
(1)下列垃圾属于有害垃圾的是 ,
A.废电池 B.碎玻璃 C.枯枝败叶 D.过期药品
(2)如图甲所示是脚踏式翻盖垃圾桶的实物图,翻盖的原理利用了杠杆,图乙所示是两个杠杆组合的示意图。桶盖的质量为800g,脚踏杆和其他连接杆的质量不计,已知O 1 A=30cm,AB=51cm,CO 2=5cm,桶盖DO2质量分布均匀,厚度不计,D为重心,桶盖闭合时,连接杆BC处于竖直状态。
①由图乙可知,DCO2为________(选填“省力”或“费力”)杠杆;
②若要把桶盖翻开,脚对踏板 A处的压力至少为________。
1.如图所示,杠杆始终处于水平平衡状态,改变弹簧测力计拉力的方向,使其从位置①到位置②,再到位置③。此过程中,弹簧测力计的示数将( ) 。
A.逐渐变大 B.逐渐变小 C.先变大后变小 D.先变小后变大
2.指甲刀是生活中常用的小工具,如图所示,它包含三个杠杆,关于这三个杠杆的说法正确的是( )
A.一个省力杠杆,两个费力杠杆 B.一个费力杠杆,两个省力杠杆
C.三个都是省力杠杆 D.三个都是费力杠杆
3.衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是( )
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
4.如图所示,作用在杠杆一端始终与杠杆垂直的力F,将杠杆缓慢匀速地由位置A拉至位置B,在这个过程中力F的大小将( )
A.变大 B.不变 C.变小 D.先变大后变小
5.如图AB为一可绕O点转动的杠杆,在A端通过绳子作用一个拉力,使杠杆平衡,保持重物不动,而使绳绕A点沿图中虚线缓慢逆时针转动,则F( )
A.先变大后变小 B.先变小后变大 C.不变 D.无法判断
6.如图所示的杠杆(自重和摩擦不计),O是支点,A处挂一重为50N的物体,为保证杠杆在水平位置平衡,在中点B处沿 (选填“F1”、“F2”或“F3”)方向施加的力最小,为 N.
7.小亮同学设计了如图所示的装置进行实验,利用小量程弹簧称测金属的密度,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________ N。
(2)被测金属块密度:ρ=________ g/cm3。
1.如图所示的杠杆AB处于平衡状态,O点为杠杆的支点,则力F力臂是( )
A.OF B.OD
C.OC D.DF
2.有一根一端粗一端细的木棒,用绳子拴住木棒的O点,将它悬挂起来,恰好处于水平位置平衡,如图所示,若把木棒从绳子悬挂处锯开,则被锯开的木棒( )
A.粗细两端一样重 B.粗端较重 C.细端较重 D.无法判定
3.如图所示,轻质杠杆0A中点悬挂一重为60牛的物体C,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是 。保持F的方向不变,将杠杆从A位置匀速提升到B位置,该过程中力F将 。
4.杆秤是一种用来测量物体质量的工具。小金尝试做了如图所示的杆秤。在秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,于是小金将此处标为0刻度。当秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡测得OA=5cm,OB=10cm。
(1)计算秤砣的质量m砣 =________ kg
(2)小金在B处标的刻度应为________kg。若图中OC=2OB,则C处的刻度应为________Kg
(3)当秤盘上放一个质量为2kg的物体时,若换用一个质量更大的秤砣,移动秤砣使杆秤再次水平平衡时,其读数________(选填“<”或“>”)2kg,由此可知一杆杄秤不能随意更换秤砣 。
5.将酒敞口放置,酒精度(酒中酒精的体积百分比)会变化吗?小科认为:只要确定酒的密度是否变化就能作出判断。于是利用身边的物品,动手制作“密度秤”来测量酒的密度。
步骤Ⅰ:按图甲制作好秤杆,提起提纽,移动秤砣(小螺母),当秤杆水平平衡时用笔将此时秤砣的悬挂点B标记为“0”刻度(单位:g/cm3)。
步骤Ⅱ:按图乙所示,将大螺母浸没在水中(大螺母必须浸没且不碰底),提起提纽,移动秤砣,当秤杆水平平衡时用笔将此时秤砣的悬挂点C标记为“1”刻度。再将BC两刻度之间分为10等份。
步骤Ⅲ:测量酒的密度。
(1).应用:小科,用该密度秤分别测出瓶盖刚打开和敞口一段时间后酒的密度约为0.92g/cm3和0.96g/cm3 ,已知酒精密度为0.8g/cm3 , 应用密度知识可判断出其酒精度 (填“变大”“不变”或“变小")。
(2).反思:在制作和测量过程中,大螺母必须浸没的目的是 。
(3).拓展:小科若要测量食盐水的密度,他应先在密度秤上增加大于1的刻度,请你写出利用直尺和笔标定刻度的过程: 。
答案及解析
例1、【答案】 ;F<G
【解析】在杠杆上,当以支点到作用点之间的线段为动力臂时最长,这时动力最小,因此找到圆周上到支点距离最远的点即可。
【解答】在圆周上,两点之间最长的就是直径。从支点做通过支点的直径,与圆周的交点就是力的作用点,然后通过它做这条直径的垂线即可。
由杠杆平衡条件,F1L1=F2L2可知,在阻力跟阻力臂的乘积一定时,动力臂越长,动力越小;元的直径作为最长力臂,由图知,动力的方向应该向上,作用点在圆的切线位置,如图,比较可知,L1>L2 , 所以F<G
例2、【答案】C
【解析】分析杠杆旋转的过程中,动力臂和阻力臂的大小关系,根据杠杆的平衡条件判断即可。
【解答】在杠杆由竖直位置转动到水平位置时,动力臂L1的长度始终不变。在开始的一端时间内,动力臂L1>L2,为省力杠杆;后来,动力臂L1<L2,为费力杠杆,因此这个杠杆先是省力的,后是费力的。
故选C。
例3、【答案】不一定;变小;
【解析】(1)阻力臂为,动力F甲的方向不确定,那么动力臂的长度可能大于,也可能小于,所以该杠杆不一定是省力杠杆;
(2)在杠杆由水平位置匀速向上提升重物的过程中,阻力G保持不变,但是阻力臂L2不断减小,动力臂L1=OA保持不变;根据杠杆的平衡条件G×L2=F乙×OA可知,动力F乙逐渐变小;
(3)如下图所示:
若动力F丙由竖直向上的方向沿逆时针缓慢地转到水平向左的方向, 当动力臂为OB时最长,即动力臂先变大后变小。根据杠杆的平衡条件G×L2=F丙×L1可知,G和L2保持不变,那么动力F丙的变化应该是先变小后变大。如下图所示:
例4、【答案】(1)A,D (2)费力;39.2N
【解析】(1)垃圾的分类有可回收垃圾、其它垃圾(干垃圾)、厨余垃圾(湿垃圾)、有害垃圾;
①可回收物主要包括废纸、塑料、玻璃、金属和布料五大类;
②其他垃圾包括除上述几类垃圾之外的砖瓦陶瓷、渣土、卫生间废纸、纸巾等难以回收的废弃物及果壳、尘土、食品袋(盒);
③厨余垃圾包括剩菜剩饭、骨头、菜根菜叶、果皮等食品类废物,
④有害垃圾含有对人体健康有害的重金属、有毒的物质或者对环境造成现实危害或者潜在危害的废弃物。
(2)①比较动力臂和阻力臂的大小,从而确定杠杆的分类;
②在杠杆DCO2上,根据杠杆的平衡条件F1L1=F2L2计算出作用在顶杆BC上的力;在杠杆AB上,再次利用杠杆的平衡条件计算出作用在A处的压力。
【解答】(1)废电池和过期药品属于有害垃圾,碎玻璃和枯枝败叶属于其它垃圾,故选AD。
(2)①对于杠杆DCO2来说,桶盖的重力相当于阻力,阻力臂为DO2;顶杆BC对桶盖的支持力为动力,动力臂为CO2,此时动力臂小于阻力臂,为费力杠杆。
②对于杠杆DCO2来说,据杠杆的平衡条件F1L1=F2L2得到:G×DO2=FCB×CO2;
0.8kg×10N/kg×(30cm+5cm)=FCB×5cm;
解得:FCB=56N;
在杠杆AB上,据杠杆的平衡条件F1L1=F2L2得到:F×AO1=FCB×BO1;
F×30cm=56N×(51cm-30cm);
解得:F=39.2N。
1.【解析】根据杠杆的平衡条件F1L1=F2L2分析。
【解答】根据杠杆的平衡条件F1L1=F2L2可知,当阻力和阻力臂保持不变时,动力与动力臂的长度成反比。根据图片可知,当测力计的拉力方向从①到③时,动力臂先变大后变小,则弹簧测力计的示数先变小后变大,故D正确,而A、B、C错误。
故选D。
2.【答案】A
【解析】根据动力臂和阻力臂的大小关系确定杠杆的种类。
①对于杠杆CBA来说,C点为支点,阻力作用在B点,动力作用在A点,此时动力臂大于阻力臂,为省力杠杆;
②对于杠杆DBO来说,支点为O,动力作用在B点,阻力作用在D点,此时动力臂小于阻力臂,为费力杠杆;
③对于杠杆DEO来说,O为支点,动力作用在E点,阻力作用在D点,此时动力臂小于阻力臂,为费力杠杆。
因此指甲刀包括一个省力杠杆,两个费力杠杆。故选A。
3.【答案】B
【解析】如果动力臂大于阻力臂,那么为省力杠杆;如果动力臂小于阻力臂,那么为费力杠杆。
夹子的轴是杠杆的支点O;
(1)当用手将其捏开时,弹簧的压力为阻力,手的压力为动力,此时动力臂大于阻力臂,为省力杠杆;
(2)当用其夹住物品时,弹簧的压力为动力,而夹口上的物体施加阻力,此时动力臂小于阻力臂,为费力杠杆。故B正确,而A、C、D错误。故选B。
4.【答案】A
【解析】注意分析杠杆改变位置的过程中,动力臂和阻力臂的变化,然后根据杠杆的平衡条件分析动力F的变化即可。
根据图片可知,物体的重力为阻力,拉力F为动力;
根据杠杆的平衡条件得到:G×L2=F×L1;
由于拉力F始终与杠杆垂直,所以动力臂L1保持不变;
在杠杆旋转的过程中,阻力臂L2逐渐增大,那么G×L2=F×L1中的乘积变大;因为L1不变,所以动力F不断增大,故A正确,而B、C、D错误。
5.【答案】B
【解析】在杠杆上,从支点到力的作用点为力臂时最长,此时动力最小;分析拉力在转动过程中动力臂的长度变化即可。
【解答】分析可知,当力F与杠杆AB垂直时,此时动力臂最长,因此在力F转动的过程中,动力臂先变长后变短;根据杠杆的平衡条件可知,力F先变小后变大。故选B。
6.【答案】:F2;100。
【解析】为使拉力最小,动力臂要最长,拉力F的方向应该垂直杠杆向上,即竖直向上(F2),动力臂为OB最长,
杠杆在水平位置平衡,根据杠杆的平衡条件:
F2×OB=G×OA,由于OA是OB的二倍,所以:F=2G=100N。
7.【答案】(1)1.8(2)3
【解析】(1)由公式:,
;
(2)由于杠杆平衡可得:
对金属块进行受力分析可知,金属受向下的重力,向上的浮力F浮和绳子对金属块向上的拉力(与F1是一对相互作用力),三力作用下金属块处于平衡状态。
,
1.【答案】C
【解析】已知O为支点,力臂是从支点O到力的作用线的距离,故左端拉力F的力臂是OC;
2.【答案】B
【解析】将悬挂点O看做支点,左边木棒的重力为阻力,右边木棒的重力为动力。根据图片可知,左端的阻力臂肯定小于右端的动力臂,根据杠杆平衡条件F1L1=F2L2可知,左端木棒的重力肯定大于右端木棒的重力,故B正确,而A、C、D错误。故选B。
3.【解析】(1)根据杠杆的平衡条件F1L1=F2L2计算。
(2)注意分析动力臂和阻力臂的比值是否发生改变即可。
【解答】(1)根据图片可知,O为支点,G为阻力,阻力臂为;F为动力,动力臂为OA。根据杠杆的平衡条件F1L1=F2L2得到:F×OA=60N×;
解得:F=30N。
(2)原来杠杆在水平位置平衡时,根据杠杆的平衡条件得到: ①;
在杠杆提升的过程中,如下图所示:
△OCC'与△OAA'相似,则 ②;
根据杠杆的平衡条件得到: ③;
①②③联立得到:F=F';
则该过程中F大小不变。
4.【解析】(1)秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡,根据杠杆平衡条件F1L1=F2L2计算秤砣的质量;
(2)秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,由此知O处为0刻度,由此知B处标的刻度值,然后根据杠杆的平衡条件F1L1=F2L2计算出C处的刻度值。
(3)根据杠杆的平衡条件F1L1=F2L2分析判断。
【解答】(1)由杠杆的平衡条件F1L1=F2L2得到:
m物g×AO=m砣g×OB; m物×AO=m砣×OB; 2kg×5cm=m砣×10cm;
解得:m砣=1kg;
(2)秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,由此知O处为0刻度,
秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡,所以在B处标的刻度应为2kg;
秤砣在C处时杆秤恰好水平平衡,此时秤盘上放的重物质量为m,
则mg×AO=m砣g×OC;
所以m×AO=m砣×2OB;
m×5cm=1kg×2×10cm;
解得:m=4kg,
所以C处刻度应为4kg。
(3)由杠杆的平衡条件可知:G物×OA=G砣×l,G物×OA的值不变,G砣增大,力臂l变小,读数变小,故读数小于2kg。
5.【解析】(1)白酒其实是酒精和水的混合液,因为水的密度大于酒精的密度,所以水越多,白酒的密度越大;酒精越多,白酒的密度越小;
(2)大螺母受到浮力的大小直接影响所测液体的密度,而浮力受到液体密度和排开液体体积的影响,根据控制变量法的要求可知,探究浮力的大小与液体密度的关系时,必须控制排开液体的体积相同;
(3)根据图片可知,液体的密度越大,刻度值越靠左,且液体的密度与刻度值成正比。B点为0,C点为1,可以根据BC的长度在C点左侧量取得到D点,这就是刻度2的位置,将CD之间平均分成10份每份就是0.1,据此刻度标注完成。也可以将CB之间平均分成10份,得到0.1的长度,据此在C点左侧依次画出对应的刻度值即可。
【解答】(1)敞口一段时间后,白酒溶液的密度增大了,说明其中的酒精减小,而水相对增多了,故酒精度变小。
(2)反思:在制作和测量过程中,大螺母必须浸没的目的是:控制排开的液体体积相同。
(3)利用直尺和笔标定刻度的过程:
方法一:先测出BC的长度,以C点为起点向左画出与BC等长的CD,再把CD长度十等分;
方法二:先测每小格的长度,以C点为起点向左画出与前面每小格等距的刻度。
2022-2023学年上学期浙教版科学九年级“冲刺重高”讲义(二十九)
杠杆的动态平衡及应用
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
