广东省广州16中2013-2014学年高一上学期入学考试数学试题
文档属性
| 名称 | 广东省广州16中2013-2014学年高一上学期入学考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-14 16:53:43 | ||
图片预览




文档简介
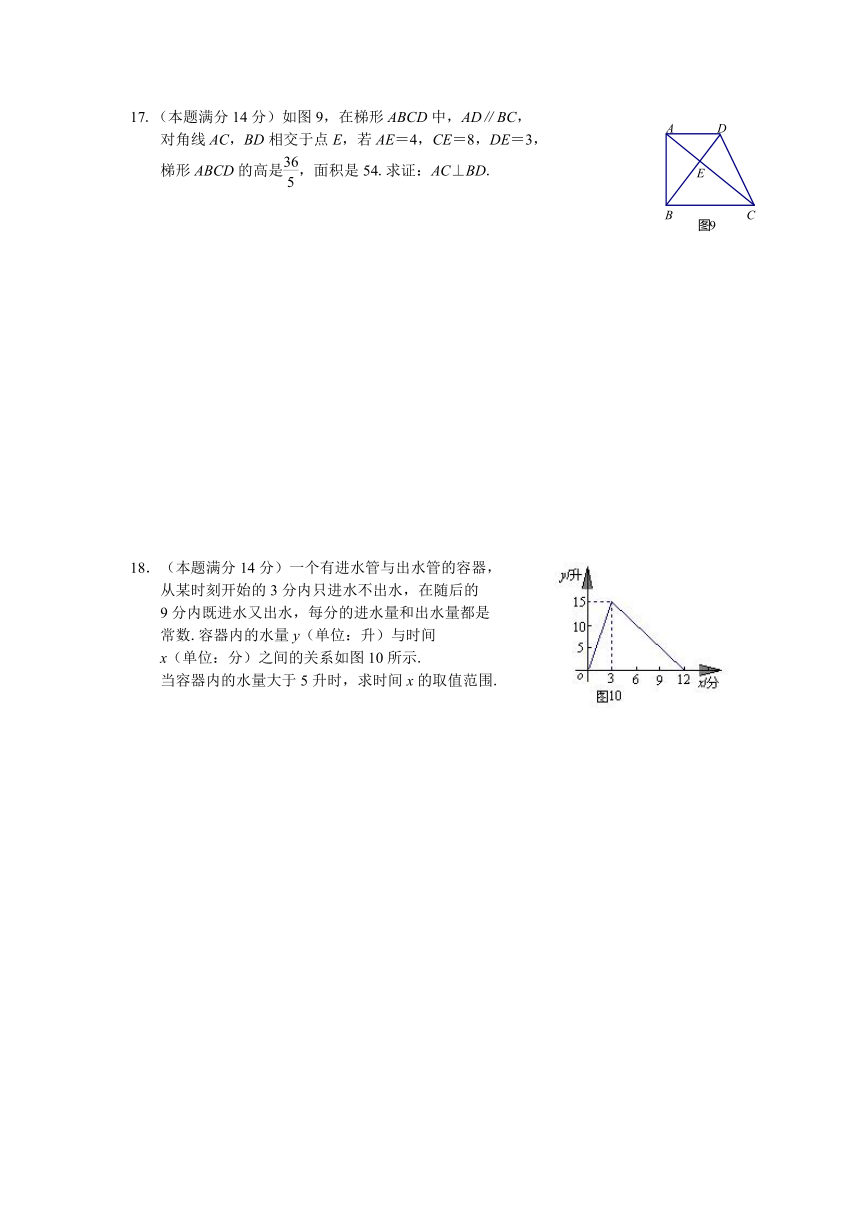
广州16中2013-2014学年高一上入学数学考试题
(试卷满分:150分 考试时间:120分钟)
班级 姓名 座位号
一、选择题(本大题有8小题,每小题5分,共40分.每小题都有四个选项,其中有且只有一个选项正确)
1.已知∠A=60°,则∠A的补角是
A.160°. B.120°.
C.60°. D.30°.
2.图1是下列一个立体图形的三视图,则这个立体图形是
A.圆锥. B.球.
C.圆柱. D.正方体.
3.掷一个质地均匀的正方体骰子,当骰子停止后,朝上
一面的点数为5的概率是
A.1. B.. C.. D.0.
4.如图2,在⊙O中,=,∠A=30°,则∠B=
A.150°. B.75°.
C.60°. D.15°.
5.方程=的解是
A.3. B.2.
C.1. D.0.
6.在平面直角坐标系中,将线段OA向左平移2个单位,平移后,点O,A的对应点分别
为点O1,A1.若点O(0,0),A(1,4),则点O1,A1的坐标分别是
A.(0,0),(1,4). B.(0,0),(3,4).
C.(-2,0),(1,4). D.(-2,0),(-1,4).
7. 已知二次函数y=2x2+9x+34,当自变量x取两个不同的值x1、x2时,函数值相等,则当自变量x取x1+x2 时的函数值与
A.x=1 时的函数值相等 B.x=0时的函数值相等
C.x=时的函数值相等 D. x=-时的函数值相等
8.已知二次函数()的图象如图所示,有下列结论:①;
②; ③3a+c<0; ④9a+3b+c>0.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题有6小题,每小题5分,共30分).
9.在实数范围内分解因式: =_________________________
10.已知:如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,
BE与AD相交于点O.写出两组相等的线段(不包括AB=CD和AD=BC).
.
11.一个口袋中装有 4个白球,1个红球,7个黄球,搅匀后随机从袋中摸出 1个球是白球的概率是 ______
12.把抛物线先向上平移2个单位,再向左平移3个单位,所得的抛物线是 ______ ;
13.为发展农业经济,致富奔小康,养鸡专业户王大伯2004年养了2000只鸡,上市前,他随机抽取了10只鸡,称得重量统计如下表:估计这批鸡(2000只)的总重量为 ______kg.
重量(单位:kg)
2
2.2
2.5
2.8
3
数量(单位:只)
1
2
4
2
1
14.已知正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1个平方单位,则点C的个数为________________个
2013学年高一入学数学考试答卷
班级 姓名 学号 成绩
二、填空题: 本大题共5小题,考生作答4小题,每小题5分,满分20分.
9、 ;10、 ;11、
12、 ;13、 ;14、
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
15.(12分)先化简,再求值: ,其中.
16. (12分)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
求证:AD⊥DC;
若AD=2,AC=,求AB的长.
17.(本题满分14分)如图9,在梯形ABCD中,AD∥BC,
对角线AC,BD相交于点E,若AE=4,CE=8,DE=3,
梯形ABCD的高是,面积是54.求证:AC⊥BD.
18.(本题满分14分)一个有进水管与出水管的容器,
从某时刻开始的3分内只进水不出水,在随后的
9分内既进水又出水,每分的进水量和出水量都是
常数.容器内的水量y(单位:升)与时间
x(单位:分)之间的关系如图10所示.
当容器内的水量大于5升时,求时间x的取值范围.
19.(本题满分14分)若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且+
=2(k是整数),则称方程x2+bx+c=0为“偶系二次方程”.如方程x2-6x-27=0,
x2-2x-8=0,x2+3x-=0,x2+6x-27=0, x2+4x+4=0都是“偶系二次方程”.
(1)判断方程x2+x-12=0是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数b,是否存在实数c,使得关于x的方程x2+bx+c=0是“偶系二次方程”,并说明理由.
20. (14分)等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE~△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
探究1:△BPE与△CFP还相似吗?(只需写出结论)
探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
设EF=m,△EPF的面积为S,试用m的代数式表示S.
2013学年高一入学数学考试答案
一、选择题(本大题共7小题,每小题3分,共21分)
BCCB ADBC
二、填空题(本大题有6小题,每小题5分,共30分).
9.
10、BC=BE AB=DE
11.
12、
13.5000
14.6
15、原式=
当时,原式=
16、(1)连接OC ∵OC=OA ∴∠CAO=∠OCA 又∵CD与圆O相切 ∴∠OCD=90° 即∠OCA+∠DCA=90° ∴∠CAO+∠DCA=90° 又∵AC平分∠DAB ∴∠DAC=∠CAO ∴∠DAC+∠DCA=90° ∴∠ADC=90° 即AD⊥DC (2)连接BC 因为AB为圆O的直径 ∴∠ACB=90° ∴∠ADC=∠ACB=90° 又∵∠DAC=∠CAO ∴△ADC∽△ACB ∴
∴AB=
17.(本题满分6分)
证明1:∵AD∥BC,
∴∠ADE=∠EBC,∠DAE=∠ECB.
∴△EDA∽△EBC. ……………………………1分
∴ ==. ……………………………2分
即:BC=2AD. ………………3分
∴54=×( AD+2AD)
∴AD=5. ………………4分
在△EDA中,
∵DE=3,AE=4,
∴DE2+AE2=AD2. ……………………………5分
∴∠AED=90°.
∴ AC⊥BD. ……………………………6分
证明2: ∵AD∥BC,
∴∠ADE=∠EBC,∠DAE=∠ECB.
∴△EDA∽△EBC. ……………………………1分
∴=. ……………………………2分
即=.
∴BE=6. ……………………………3分
过点D作DF∥AC交BC的延长线于点F.
由于AD∥BC,
∴四边形ACFD是平行四边形.
∴DF=AC=12,AD=CF.
∴BF=BC+AD.
∴54=××BF.
∴BF=15. ……………………………4分
在△DBF中,
∵DB=9,DF=12,BF=15,
∴DB2+DF2=BF2. ……………………………5分
∴∠BDF=90°.
∴DF⊥BD.
∴AC⊥BD. ……………………………6分
18.(本题满分6分)
解1: 当0≤x≤3时,y=5x. ……………………………1分
当y>5时,5x>5, ……………………………2分
解得 x>1.
∴1<x≤3. ……………………………3分
当3<x≤12时,
设 y=kx+b.
则解得
∴ y=-x+20. ……………………………4分
当y>5时,-x+20>5, ……………………………5分
解得 x<9.
∴ 3<x<9. ……………………………6分
∴容器内的水量大于5升时,1<x<9 .
解2: 当0≤x≤3时,y=5x. ……………………………1分
当y=5时,有5=5x,解得 x=1.
∵ y随x的增大而增大,
∴当y>5时,有x>1. ……………………………2分
∴ 1<x≤3. ……………………………3分
当3<x≤12时,
设 y=kx+b.
则解得
∴ y=-x+20. ……………………………4分
当y=5时,5=-x+20.
解得x=9.
∵ y随x的增大而减小,
∴当y>5时,有x<9. ……………………………5分
∴3<x<9. ……………………………6分
∴容器内的水量大于5升时,1<x<9 .
19.(本题满分11分)
(1)解: 不是 ……………………………1分
解方程x2+x-12=0得,x1=-4,x2=3. ……………………………2分
+=4+3=2×. ……………………………3分
∵3.5不是整数,
∴方程x2+x-12=0不是“偶系二次方程”.…………………………4分
(2)解:存在 …………………………6分
∵方程x2-6x-27=0,x2+6x-27=0是“偶系二次方程”,
∴ 假设 c=mb2+n. …………………………8分
当 b=-6,c=-27时,有 -27=36m+n.
∵x2=0是“偶系二次方程”,
∴n=0,m=- . …………………………9分
即有c=- b2.
又∵x2+3x-=0也是“偶系二次方程”,
当b=3时,c=- ×32=-.
∴可设c=- b2. …………………………10分
对任意一个整数b,当c=- b2时,
∵△=b2-4c
=4b2.
∴ x= .
∴ x1=-b,x2=b.
∴ +=+=2.
∵b是整数,∴对任意一个整数b,当c=- b2时,关于x的方程
x2+bx+c=0是“偶系二次方程”. …………………………11分
(试卷满分:150分 考试时间:120分钟)
班级 姓名 座位号
一、选择题(本大题有8小题,每小题5分,共40分.每小题都有四个选项,其中有且只有一个选项正确)
1.已知∠A=60°,则∠A的补角是
A.160°. B.120°.
C.60°. D.30°.
2.图1是下列一个立体图形的三视图,则这个立体图形是
A.圆锥. B.球.
C.圆柱. D.正方体.
3.掷一个质地均匀的正方体骰子,当骰子停止后,朝上
一面的点数为5的概率是
A.1. B.. C.. D.0.
4.如图2,在⊙O中,=,∠A=30°,则∠B=
A.150°. B.75°.
C.60°. D.15°.
5.方程=的解是
A.3. B.2.
C.1. D.0.
6.在平面直角坐标系中,将线段OA向左平移2个单位,平移后,点O,A的对应点分别
为点O1,A1.若点O(0,0),A(1,4),则点O1,A1的坐标分别是
A.(0,0),(1,4). B.(0,0),(3,4).
C.(-2,0),(1,4). D.(-2,0),(-1,4).
7. 已知二次函数y=2x2+9x+34,当自变量x取两个不同的值x1、x2时,函数值相等,则当自变量x取x1+x2 时的函数值与
A.x=1 时的函数值相等 B.x=0时的函数值相等
C.x=时的函数值相等 D. x=-时的函数值相等
8.已知二次函数()的图象如图所示,有下列结论:①;
②; ③3a+c<0; ④9a+3b+c>0.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题有6小题,每小题5分,共30分).
9.在实数范围内分解因式: =_________________________
10.已知:如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,
BE与AD相交于点O.写出两组相等的线段(不包括AB=CD和AD=BC).
.
11.一个口袋中装有 4个白球,1个红球,7个黄球,搅匀后随机从袋中摸出 1个球是白球的概率是 ______
12.把抛物线先向上平移2个单位,再向左平移3个单位,所得的抛物线是 ______ ;
13.为发展农业经济,致富奔小康,养鸡专业户王大伯2004年养了2000只鸡,上市前,他随机抽取了10只鸡,称得重量统计如下表:估计这批鸡(2000只)的总重量为 ______kg.
重量(单位:kg)
2
2.2
2.5
2.8
3
数量(单位:只)
1
2
4
2
1
14.已知正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1个平方单位,则点C的个数为________________个
2013学年高一入学数学考试答卷
班级 姓名 学号 成绩
二、填空题: 本大题共5小题,考生作答4小题,每小题5分,满分20分.
9、 ;10、 ;11、
12、 ;13、 ;14、
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
15.(12分)先化简,再求值: ,其中.
16. (12分)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
求证:AD⊥DC;
若AD=2,AC=,求AB的长.
17.(本题满分14分)如图9,在梯形ABCD中,AD∥BC,
对角线AC,BD相交于点E,若AE=4,CE=8,DE=3,
梯形ABCD的高是,面积是54.求证:AC⊥BD.
18.(本题满分14分)一个有进水管与出水管的容器,
从某时刻开始的3分内只进水不出水,在随后的
9分内既进水又出水,每分的进水量和出水量都是
常数.容器内的水量y(单位:升)与时间
x(单位:分)之间的关系如图10所示.
当容器内的水量大于5升时,求时间x的取值范围.
19.(本题满分14分)若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且+
=2(k是整数),则称方程x2+bx+c=0为“偶系二次方程”.如方程x2-6x-27=0,
x2-2x-8=0,x2+3x-=0,x2+6x-27=0, x2+4x+4=0都是“偶系二次方程”.
(1)判断方程x2+x-12=0是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数b,是否存在实数c,使得关于x的方程x2+bx+c=0是“偶系二次方程”,并说明理由.
20. (14分)等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE~△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
探究1:△BPE与△CFP还相似吗?(只需写出结论)
探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
设EF=m,△EPF的面积为S,试用m的代数式表示S.
2013学年高一入学数学考试答案
一、选择题(本大题共7小题,每小题3分,共21分)
BCCB ADBC
二、填空题(本大题有6小题,每小题5分,共30分).
9.
10、BC=BE AB=DE
11.
12、
13.5000
14.6
15、原式=
当时,原式=
16、(1)连接OC ∵OC=OA ∴∠CAO=∠OCA 又∵CD与圆O相切 ∴∠OCD=90° 即∠OCA+∠DCA=90° ∴∠CAO+∠DCA=90° 又∵AC平分∠DAB ∴∠DAC=∠CAO ∴∠DAC+∠DCA=90° ∴∠ADC=90° 即AD⊥DC (2)连接BC 因为AB为圆O的直径 ∴∠ACB=90° ∴∠ADC=∠ACB=90° 又∵∠DAC=∠CAO ∴△ADC∽△ACB ∴
∴AB=
17.(本题满分6分)
证明1:∵AD∥BC,
∴∠ADE=∠EBC,∠DAE=∠ECB.
∴△EDA∽△EBC. ……………………………1分
∴ ==. ……………………………2分
即:BC=2AD. ………………3分
∴54=×( AD+2AD)
∴AD=5. ………………4分
在△EDA中,
∵DE=3,AE=4,
∴DE2+AE2=AD2. ……………………………5分
∴∠AED=90°.
∴ AC⊥BD. ……………………………6分
证明2: ∵AD∥BC,
∴∠ADE=∠EBC,∠DAE=∠ECB.
∴△EDA∽△EBC. ……………………………1分
∴=. ……………………………2分
即=.
∴BE=6. ……………………………3分
过点D作DF∥AC交BC的延长线于点F.
由于AD∥BC,
∴四边形ACFD是平行四边形.
∴DF=AC=12,AD=CF.
∴BF=BC+AD.
∴54=××BF.
∴BF=15. ……………………………4分
在△DBF中,
∵DB=9,DF=12,BF=15,
∴DB2+DF2=BF2. ……………………………5分
∴∠BDF=90°.
∴DF⊥BD.
∴AC⊥BD. ……………………………6分
18.(本题满分6分)
解1: 当0≤x≤3时,y=5x. ……………………………1分
当y>5时,5x>5, ……………………………2分
解得 x>1.
∴1<x≤3. ……………………………3分
当3<x≤12时,
设 y=kx+b.
则解得
∴ y=-x+20. ……………………………4分
当y>5时,-x+20>5, ……………………………5分
解得 x<9.
∴ 3<x<9. ……………………………6分
∴容器内的水量大于5升时,1<x<9 .
解2: 当0≤x≤3时,y=5x. ……………………………1分
当y=5时,有5=5x,解得 x=1.
∵ y随x的增大而增大,
∴当y>5时,有x>1. ……………………………2分
∴ 1<x≤3. ……………………………3分
当3<x≤12时,
设 y=kx+b.
则解得
∴ y=-x+20. ……………………………4分
当y=5时,5=-x+20.
解得x=9.
∵ y随x的增大而减小,
∴当y>5时,有x<9. ……………………………5分
∴3<x<9. ……………………………6分
∴容器内的水量大于5升时,1<x<9 .
19.(本题满分11分)
(1)解: 不是 ……………………………1分
解方程x2+x-12=0得,x1=-4,x2=3. ……………………………2分
+=4+3=2×. ……………………………3分
∵3.5不是整数,
∴方程x2+x-12=0不是“偶系二次方程”.…………………………4分
(2)解:存在 …………………………6分
∵方程x2-6x-27=0,x2+6x-27=0是“偶系二次方程”,
∴ 假设 c=mb2+n. …………………………8分
当 b=-6,c=-27时,有 -27=36m+n.
∵x2=0是“偶系二次方程”,
∴n=0,m=- . …………………………9分
即有c=- b2.
又∵x2+3x-=0也是“偶系二次方程”,
当b=3时,c=- ×32=-.
∴可设c=- b2. …………………………10分
对任意一个整数b,当c=- b2时,
∵△=b2-4c
=4b2.
∴ x= .
∴ x1=-b,x2=b.
∴ +=+=2.
∵b是整数,∴对任意一个整数b,当c=- b2时,关于x的方程
x2+bx+c=0是“偶系二次方程”. …………………………11分
同课章节目录
