21.4实际问题与二次函数(1) 课件(共25张PPT)
文档属性
| 名称 | 21.4实际问题与二次函数(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
沪科版 九年级上册
21.4实际问题与二次函数(1)
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
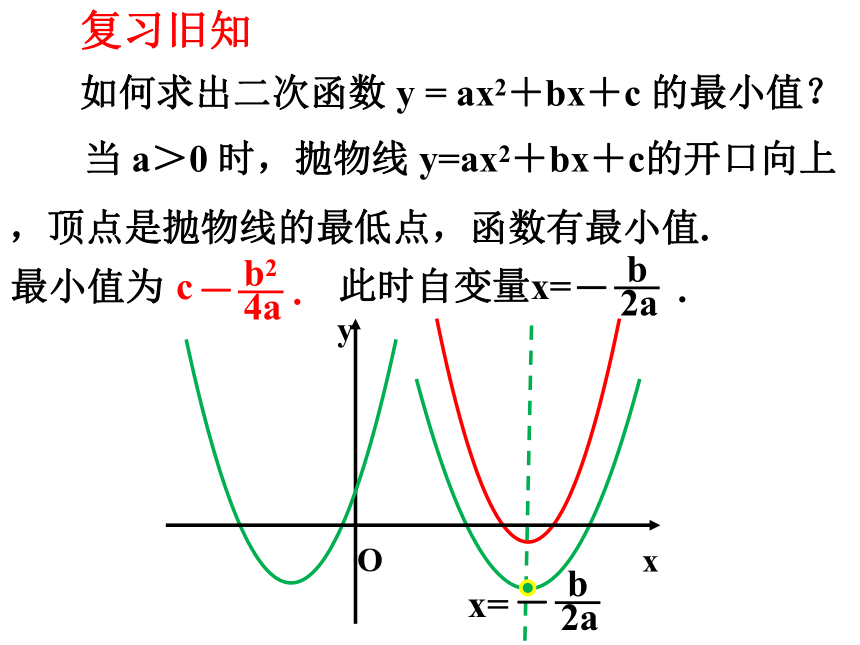
x
y
O
b
2a
-
x=
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
c
b2
4a
- .
最小值为
如何求出二次函数 y = ax2+bx+c 的最小值?
此时自变量x=
b
2a
- .
复习旧知
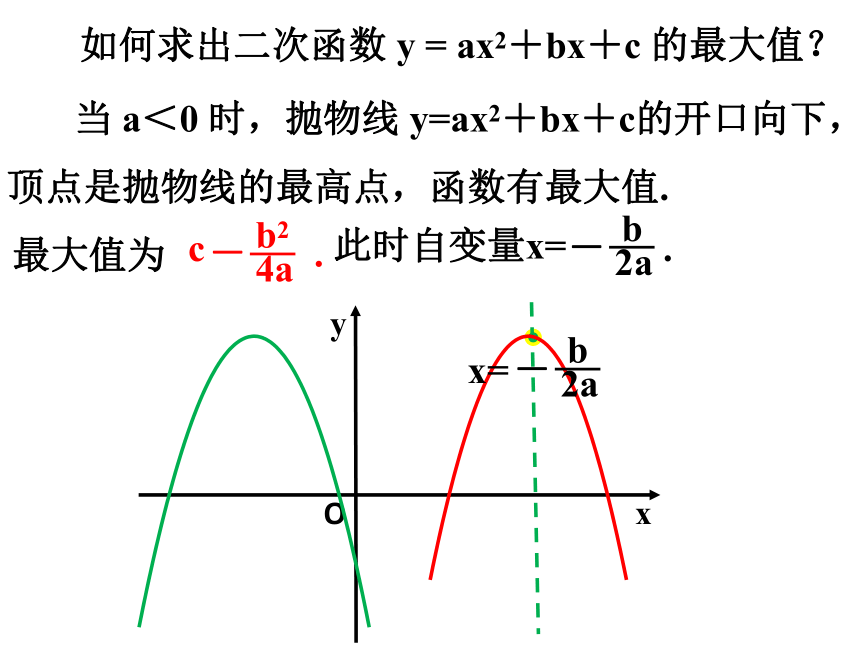
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
- .
最大值为
如何求出二次函数 y = ax2+bx+c 的最大值?
此时自变量x=
b
2a
- .
b
2a
-
x=
解:
x =
b
2a
-
=
-4
2×2
=1
-
= -3
∵ b=-4 ,c=-1,
c
b2
4a
-
=
(-4)2
4×2
-1-
∵ a=2>0 ,
① y=2x2-4x-1, ② y =-3x2+12x-8
①
求出下列函数的最大值或最小值,并求出相应的x值.
∴函数有最小值.
∴最小值y=
相应的x值为
解:
x =
b
2a
-
=
12
2×(-3)
=2
-
=4
∵ b=12 ,c=-8,
c
b2
4a
-
=
122
4×(-3)
-8-
∵ a=-3<0 ,
① y=2x2-4x-1, ② y =-3x2+12x-8
②
求出下列函数的最大值或最小值,并求出相应的x值.
∴函数有最大值.
∴最大值y=
相应的x值为
某水产养殖户用长40m的围网,在水库中围一块矩形水面,投放鱼苗,要使围成的水面面积最大,则它的边长应是多少米?
①你能够画一个周长为40m的矩形吗?
②周长为40m的矩形是唯一的吗?
③有没有一个矩形的面积是最大呢?
最大面积为多少?
④你将用什么数学知识说服大家,你所画的
矩形面积最大?
⑤利用函数图像可以求出面积的最大值吗?
例题解析
某水产养殖户用长40m的围网,在水库中围一块矩形水面,投放鱼苗,要使围成的水面面积最大,则它的边长应是多少米?
解:设围成的水面的长为x米,围成的水面面积为y平方米,矩形的周长为40米,所以它的宽应是 米.
(20-x)
根据题意,得
=20x-x2
=-x2+20x
x(20-x)
y =
(0<x<20).
解:设围成的水面的长为x米,围成的水面面积为y平方米,矩形的周长为40米,所以它的宽应是(20-x)米.
根据题意,得
=-x2+20x
x(20-x)
y =
∵ a=-1<0 ,
∵ b=20,
∴ 这个函数有最大值,
当 x=10时,
y =-102 +20×10
=
且当 x= 时,
b
2a
-
y取得最大值.
∴x=
b
2a
-
-
20
2×(-1)
=10
=100
=20x-x2
答:当围成的矩形水面边长都是10米时,面积最大,
最大面积为100平方米.
整理,得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
解: ,
∴当 时,
S 有最大值.
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
S=
60
2
-
l
l
S=
-l 2+30l
∵ a=-1<0 ,
S 最大值=
l=
b
2a
-
=
-
30
2×(-1)
=15
-152+30×15
=225.
( )
2.在直角三角形中,两直角边之和为10.问当两直角边
的边长各是多少时,这个三角形的面积最大?最大
面积是多少?
设其中一直角边长为x,则另一直角边长为
(10-x).
根据题意,得
面积为 y.
y =
2
1
(10-x)x
= -
2
1
(x2-10x)
= -
2
1
(x2-10x+25 -25)
解:
=-
2
1
(x-5)2
+
2
25
∴ y有最大值.
∵ a=- <0 ,
2
1
且当 x= 5 时,
y取得最大值.
最大面积是 .
2
25
应用二次函数解决面积最优化问题的方法:
(1)利用几何图形的面积公式得到关于面积的二次函数表达式;
(2)将二次函数表达式配方,化成顶点式 y=a(x+h)2+k;
(3)根据顶点式,结合x的取值范围,确定函数y的最值,从而确定最方法优方案.
方法总结
一玩具厂,有装配工15人,规定每人每天应装配玩具190个,但如果每增加一人,那么每人每天可少装配10个.问增加多少人可使每天装配总数最多?最多时是多少个?
解:设增加x人,装配总数为y个
由题意,得:y=
(190-10x)
(15+x)
= -10x2+40x+2850
= 2850-150x+190x-10x2
解:设增加x人,装配总数为y个,
由题意,得:
(190-10x)
(15+x)
=-10x2+40x+2850
= 2850-150x+190x-10x2
∵ a=-10<0 ,
∵ b=40,
∴ 这个函数有最大值,
当 x=2 时,
y =-10×22 +40×2+2850
=
且当x= 时,
b
2a
-
y取得最大值.
∴x=
b
2a
-
-
40
2×(-10)
=2
=2890
y=
答:增加2人可使每天装配总数最多;最多时是2890个.
解:设增加x人,装配总数为y个,
由题意,得:
(190-10x)
(15+x)
=-10x2+40x+2850
= 2850-150x+190x-10x2
∵ a=-10<0 ,
∴ 这个函数有最大值,
且当x= 2 时,
y取得最大值.
最大值为2890.
y=
答:增加2人可使每天装配总数最多;最多时是2890个.
=-10(x-2)2+2890
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
解:
(1)
y=
40
2
- x
x
=-
+20x
(0<x<25).
∴ y有最大值.
∵ a=- <0 ,
y最大值
=-
×202
+20×20
=
200(m2).
(2)
当x是 20 m 时,绿化带的面积 S 最大.
2
x2
1
2
1
∵ b=20,
=
且当 x= 时,
b
2a
-
∴x=
b
2a
-
-
20
2×(- )
=20
y取得最大值.
2
1
2
1
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
课堂小结
本节课是在学生学习完二次函数的图象和性质的知识的基础上的进一步拓展与应用.
课件说明
1.某公司准备修建一个长方体的环保型污水处理
池, 池底矩形的周长为100m,则池底的最大
面积是( ).
A.600 m B.625 m C.650 m D. 675 m .
巩固提高
B
2.如图,小明想用16m的篱笆AB(虚线部分),借
助互相垂直的两面墙围成一个矩形花园ABCD,
则花园的最大面积是( ).
A. 60 m B.63 m C.64 m D. 66 m
C
A
B
C
D
3.如图,口ABCD 的周长为10cm, ∠ B=30°,
AB=xcm.设口ABCD的面积为ycm.y与x之间
的函数表达式为 ,自变
量x的取值范围是 ;当x 时,
口ABCD的面积最大,最大面积是 .
A
B
C
D
y=- x2+ x
2
1
2
5
0<x<5
2
5
=
8
25
cm2
今天作业
课本P42页第1题
课本P57页第8题
课本P59页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.4实际问题与二次函数(1)
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
x
y
O
b
2a
-
x=
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
c
b2
4a
- .
最小值为
如何求出二次函数 y = ax2+bx+c 的最小值?
此时自变量x=
b
2a
- .
复习旧知
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
- .
最大值为
如何求出二次函数 y = ax2+bx+c 的最大值?
此时自变量x=
b
2a
- .
b
2a
-
x=
解:
x =
b
2a
-
=
-4
2×2
=1
-
= -3
∵ b=-4 ,c=-1,
c
b2
4a
-
=
(-4)2
4×2
-1-
∵ a=2>0 ,
① y=2x2-4x-1, ② y =-3x2+12x-8
①
求出下列函数的最大值或最小值,并求出相应的x值.
∴函数有最小值.
∴最小值y=
相应的x值为
解:
x =
b
2a
-
=
12
2×(-3)
=2
-
=4
∵ b=12 ,c=-8,
c
b2
4a
-
=
122
4×(-3)
-8-
∵ a=-3<0 ,
① y=2x2-4x-1, ② y =-3x2+12x-8
②
求出下列函数的最大值或最小值,并求出相应的x值.
∴函数有最大值.
∴最大值y=
相应的x值为
某水产养殖户用长40m的围网,在水库中围一块矩形水面,投放鱼苗,要使围成的水面面积最大,则它的边长应是多少米?
①你能够画一个周长为40m的矩形吗?
②周长为40m的矩形是唯一的吗?
③有没有一个矩形的面积是最大呢?
最大面积为多少?
④你将用什么数学知识说服大家,你所画的
矩形面积最大?
⑤利用函数图像可以求出面积的最大值吗?
例题解析
某水产养殖户用长40m的围网,在水库中围一块矩形水面,投放鱼苗,要使围成的水面面积最大,则它的边长应是多少米?
解:设围成的水面的长为x米,围成的水面面积为y平方米,矩形的周长为40米,所以它的宽应是 米.
(20-x)
根据题意,得
=20x-x2
=-x2+20x
x(20-x)
y =
(0<x<20).
解:设围成的水面的长为x米,围成的水面面积为y平方米,矩形的周长为40米,所以它的宽应是(20-x)米.
根据题意,得
=-x2+20x
x(20-x)
y =
∵ a=-1<0 ,
∵ b=20,
∴ 这个函数有最大值,
当 x=10时,
y =-102 +20×10
=
且当 x= 时,
b
2a
-
y取得最大值.
∴x=
b
2a
-
-
20
2×(-1)
=10
=100
=20x-x2
答:当围成的矩形水面边长都是10米时,面积最大,
最大面积为100平方米.
整理,得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地的面积 S 最大?
解: ,
∴当 时,
S 有最大值.
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
S=
60
2
-
l
l
S=
-l 2+30l
∵ a=-1<0 ,
S 最大值=
l=
b
2a
-
=
-
30
2×(-1)
=15
-152+30×15
=225.
( )
2.在直角三角形中,两直角边之和为10.问当两直角边
的边长各是多少时,这个三角形的面积最大?最大
面积是多少?
设其中一直角边长为x,则另一直角边长为
(10-x).
根据题意,得
面积为 y.
y =
2
1
(10-x)x
= -
2
1
(x2-10x)
= -
2
1
(x2-10x+25 -25)
解:
=-
2
1
(x-5)2
+
2
25
∴ y有最大值.
∵ a=- <0 ,
2
1
且当 x= 5 时,
y取得最大值.
最大面积是 .
2
25
应用二次函数解决面积最优化问题的方法:
(1)利用几何图形的面积公式得到关于面积的二次函数表达式;
(2)将二次函数表达式配方,化成顶点式 y=a(x+h)2+k;
(3)根据顶点式,结合x的取值范围,确定函数y的最值,从而确定最方法优方案.
方法总结
一玩具厂,有装配工15人,规定每人每天应装配玩具190个,但如果每增加一人,那么每人每天可少装配10个.问增加多少人可使每天装配总数最多?最多时是多少个?
解:设增加x人,装配总数为y个
由题意,得:y=
(190-10x)
(15+x)
= -10x2+40x+2850
= 2850-150x+190x-10x2
解:设增加x人,装配总数为y个,
由题意,得:
(190-10x)
(15+x)
=-10x2+40x+2850
= 2850-150x+190x-10x2
∵ a=-10<0 ,
∵ b=40,
∴ 这个函数有最大值,
当 x=2 时,
y =-10×22 +40×2+2850
=
且当x= 时,
b
2a
-
y取得最大值.
∴x=
b
2a
-
-
40
2×(-10)
=2
=2890
y=
答:增加2人可使每天装配总数最多;最多时是2890个.
解:设增加x人,装配总数为y个,
由题意,得:
(190-10x)
(15+x)
=-10x2+40x+2850
= 2850-150x+190x-10x2
∵ a=-10<0 ,
∴ 这个函数有最大值,
且当x= 2 时,
y取得最大值.
最大值为2890.
y=
答:增加2人可使每天装配总数最多;最多时是2890个.
=-10(x-2)2+2890
为了改善小区环境,某小区决定要在一块一边靠墙(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m2.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件的绿化带的面积最大?
D
C
B
A
25 m
解:
(1)
y=
40
2
- x
x
=-
+20x
(0<x<25).
∴ y有最大值.
∵ a=- <0 ,
y最大值
=-
×202
+20×20
=
200(m2).
(2)
当x是 20 m 时,绿化带的面积 S 最大.
2
x2
1
2
1
∵ b=20,
=
且当 x= 时,
b
2a
-
∴x=
b
2a
-
-
20
2×(- )
=20
y取得最大值.
2
1
2
1
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
课堂小结
本节课是在学生学习完二次函数的图象和性质的知识的基础上的进一步拓展与应用.
课件说明
1.某公司准备修建一个长方体的环保型污水处理
池, 池底矩形的周长为100m,则池底的最大
面积是( ).
A.600 m B.625 m C.650 m D. 675 m .
巩固提高
B
2.如图,小明想用16m的篱笆AB(虚线部分),借
助互相垂直的两面墙围成一个矩形花园ABCD,
则花园的最大面积是( ).
A. 60 m B.63 m C.64 m D. 66 m
C
A
B
C
D
3.如图,口ABCD 的周长为10cm, ∠ B=30°,
AB=xcm.设口ABCD的面积为ycm.y与x之间
的函数表达式为 ,自变
量x的取值范围是 ;当x 时,
口ABCD的面积最大,最大面积是 .
A
B
C
D
y=- x2+ x
2
1
2
5
0<x<5
2
5
=
8
25
cm2
今天作业
课本P42页第1题
课本P57页第8题
课本P59页第9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
