21.5反比例函数的图象和性质(4) 课件(共28张PPT)
文档属性
| 名称 | 21.5反比例函数的图象和性质(4) 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 09:04:41 | ||
图片预览




文档简介
(共28张PPT)
沪科版 九年级上册
21.5反比例函数的图象和性质(4)
教学目标:
1.理解反比例函数的比例常数k的几何意义,会用k的几何意义求相关的图形面积;
2.结合实例引导学生理解k的几何意义,是从感性认识到理性认识的转化过程,发展学生的思维.
教学重点:理解和领会反比例函数的几何意义;
教学难点:图象不在第一象限时的线段长的表示.
1.反比例函数的定义
若两个变量x、y之间可以表示成y= ( k是常数,k≠0),则称y是x反比例函数.
反比例函数的解析式可以写成 , 或写成 的形式.它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数 .
k
x
xy=k(k≠0)
y=kx-1
k
复习旧知
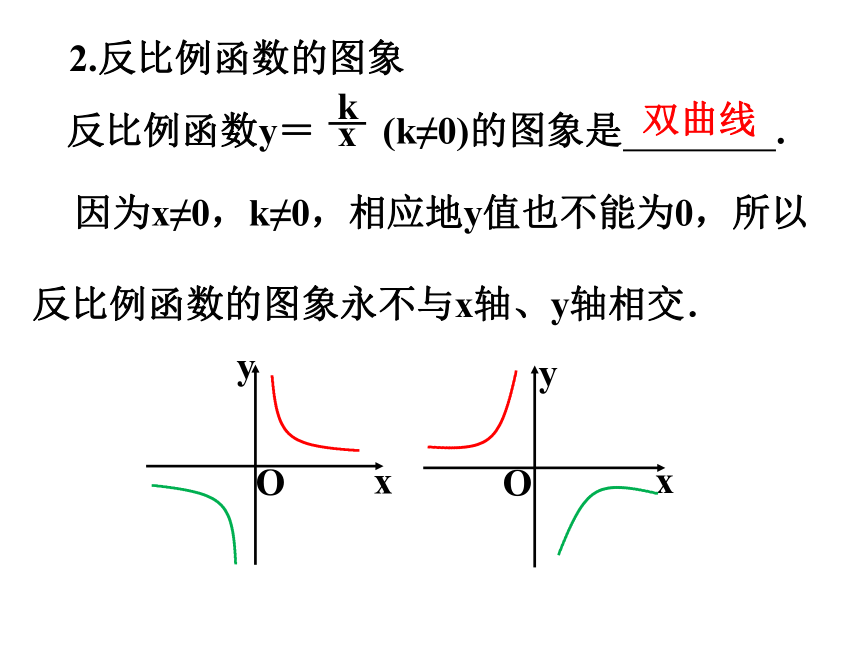
2.反比例函数的图象
反比例函数y= (k≠0)的图象是 .
双曲线
k
x
因为x≠0,k≠0,相应地y值也不能为0,所以反比例函数的图象永不与x轴、y轴相交.
x
O
y
x
O
y
3.反比例函数的性质
当k > 0时,图象分布在第 象限,在每个象限内,y随的增大x而 ;
当k < 0时,图象分布在第 象限,在每个象限内,y随x的增大而 .
一、三
减小
二、四
增大
k>0
k < 0
图象
性质
所在
象限
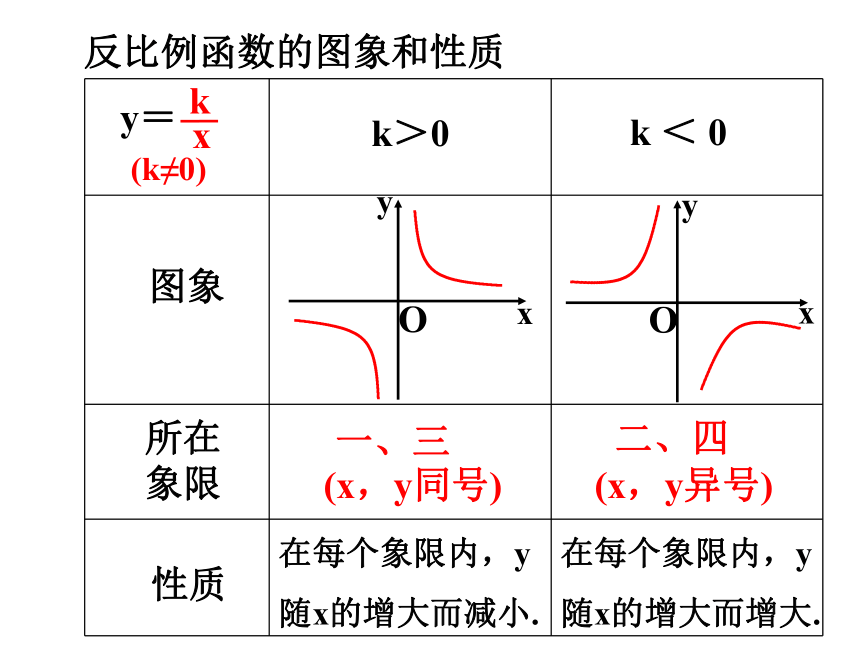
一、三
二、四
在每个象限内,y随x的增大而减小.
在每个象限内,y随x的增大而增大.
y=
k
x
(k≠0)
x
O
y
x
O
y
(x,y同号)
(x,y异号)
反比例函数的图象和性质
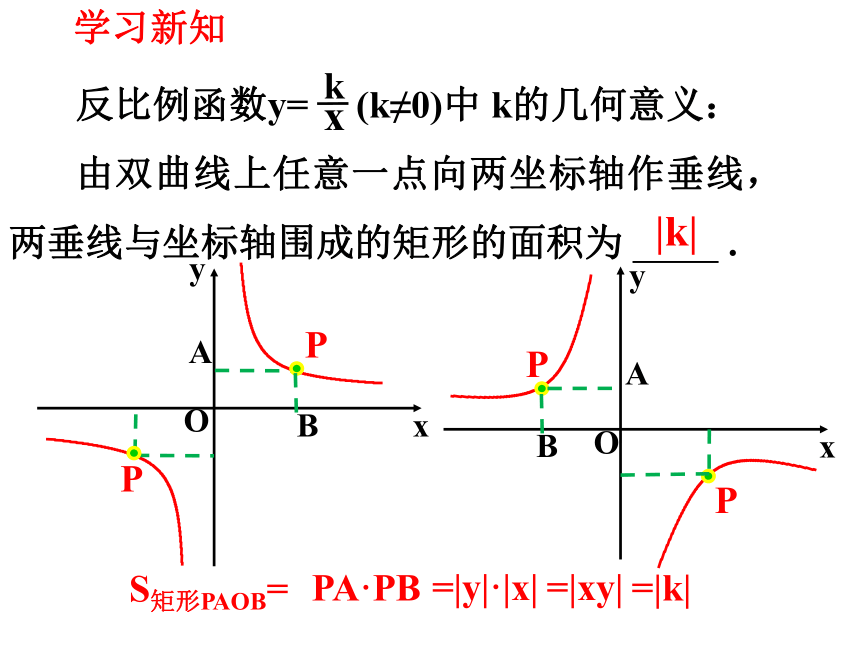
反比例函数y= (k≠0)中 k的几何意义:
由双曲线上任意一点向两坐标轴作垂线,两垂线与坐标轴围成的矩形的面积为 .
k
x
|k|
x
O
y
A
B
P
P
x
O
y
A
B
P
P
S矩形PAOB=
=|xy|
=|y|·|x|
=|k|
PA·PB
学习新知
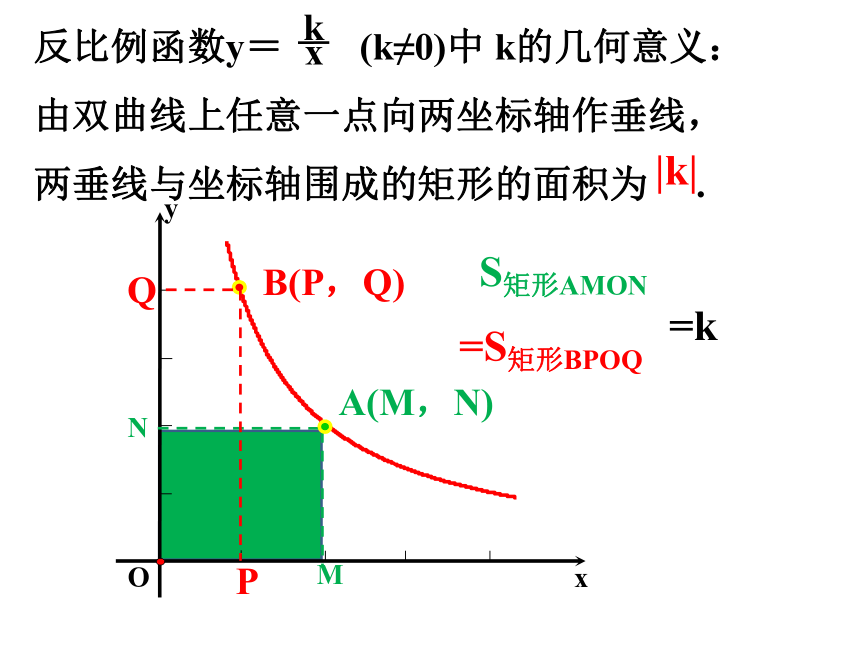
反比例函数y= (k≠0)中 k的几何意义:
由双曲线上任意一点向两坐标轴作垂线,
两垂线与坐标轴围成的矩形的面积为 .
O
y
x
M
N
A(M,N)
k
x
B(P,Q)
P
Q
S矩形AMON
=S矩形BPOQ
=k
|k|
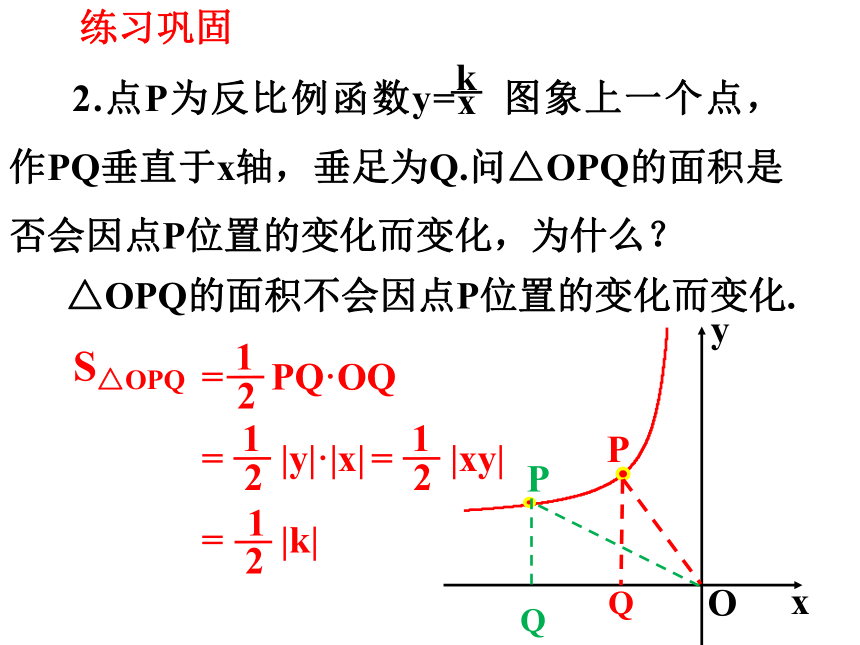
2.点P为反比例函数y= 图象上一个点, 作PQ垂直于x轴,垂足为Q.问△OPQ的面积是否会因点P位置的变化而变化,为什么?
k
x
x
O
y
P
Q
P
S△OPQ
= |xy|
= |y|·|x|
= |k|
= PQ·OQ
1
2
1
2
1
2
1
2
△OPQ的面积不会因点P位置的变化而变化.
Q
练习巩固
3.如图,点A是反比例函数y= (x>0)图象上任意一点, AB平行于x轴交反比例函数y=- (x<0)的图象于点B,作以AB为边的平行四边形ABCD,其顶点C,D在x轴上,则S□ABCD为多少?
2
x
3
x
x
O
y
A
B
C
D
y=
2
x
y=-
3
x
F
E
G
过点A作AE垂直x轴,垂足为E,
过点B作BF垂直x轴,垂足为F,
则有△AED≌△BFC (HL)
x
O
y
A
B
C
D
y=
2
x
y=-
3
x
F
E
G
∴ S□ABCD
=S矩形BFOG
+S矩形AEOG
过点A作AE垂直x轴,垂足为E,
过点B作BF垂直x轴,垂足为F,
则有△AED≌△BFC (HL)
=BF·OF
+ AE·OE
=3+2
=5
5.如图,点A,B是反比例函数y= 图象上的两点,
9
x
x
O
y
A
y=
9
x
B
分别过点A,B作AE作x轴、y轴的垂线,
构成图中的三个相邻且不重叠的小矩形S1,S2,S3.
已知S2=3,求S1+S3的值
S1
S2
S3
解:
∵ S1+S2
=9
S2+S3
=9
∴ S1+2S2+S3
=18
∵ S2=3,
∴ S1+S3
=12.
例1 如图,两个反比例函数 y= 和 y=- 的图象分别是 L1 和 L2.设点 P 在 L1 上,PC⊥x 轴,垂足为 C,交L2 于点 A;PD⊥y 轴,垂足为 D,交L2 于点 B,则△PAB 的面积为( ).
1
x
2
x
A.3 B.4
C. D.5
x
y
P
A
O
B
C
D
L2
L1
9
2
C
(a, )
1
a
(a,- )
2
a
(-2a, )
1
a
PA=
1
a
-
-
2
a
( )
=
3
a
PB =
a
-
-
2a
( )
=3a
x
O
y
A
B
C
D
y=
k
x
y=-
3k
x
P
Q
y=2t
x=t
( ,2t)
k
2t
( ,2t)
-
3k
2t
(t, )
k
t
(t, )
-
3k
t
CD=
-
=
k
2t
( )
-
3k
2t
2k
t
AB=
-
=
k
t
( )
-
3k
t
4k
t
S△PCD
= ·
1
2
2k
t
2t
=2k
S△QAB
= ·
1
2
4k
t
t
=2k
例2 如图,一次函数 y=ax+b 的图象与反比例函数
的图象交于第一象限 C,D 两点,与坐标轴交于
A、B 两点,连接 OC,OD(O 是坐标原点).
① 利用图中条件,求反比例函数的解析式和 m 的值;
② 双曲线上是否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明,并求出点 P 的坐标;若不存在,说明理由.
O
x
A
B
C(1,4)
y
D(4,m)
y=
k
x
∵ 的图象经过点 C(1,4).
例2 如图,一次函数 y=ax+b 的图象与反比例函数
的图象交于第一象限 C,D 两点,与坐标轴交于
A、B 两点,连接 OC,OD(O 是坐标原点).
① 利用图中条件,求反比例函数的解析式和 m 的值;
O
x
A
B
C(1,4)
y
D(4,m)
y=
k
x
y=
k
x
∴ 4 = .
k
1
∴ k =4 .
∴ y = .
4
x
∴当x=4时,
m=
4
4
=1 .
①
② 双曲线上是否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明,并求出点 P 的坐标;若不存在,说明理由.
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ y=ax+b的图象经过点 C(1,4),D(4,1).
a+b =4 ,
4a+b =1 ,
a =-1
∴y =-x+5 ,
∴A(5,0),B(0,5)
∴ OA =OB .
双曲线上存在一点 P,使得△POC和△POD 的面积相等.
∴
b=5.
∴
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ y=ax+b的图象经过点 C(1,4),D(4,1).
∴ a+b =4 ,
4a+b =1 ,
∴ a =-1 ,b=5.
∴y =-x+5 ,
∴A(5,0),B(0,5),
∴ OA =OB .
双曲线上存在一点 P,使得△POC 和△POD 的面积相等.
过点 O作OP⊥AB,交双曲线于点P.
连接PC、PD,
则PC=PD.
∵ OC =OD,OP=OP .
∴ △OPC ≌△OPD .
∴ S△OPC =S△OPD .
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ OP⊥AB,
yAB =-x+5 ,
∴ yOP =x
∵ y=x,
∴ x = .
4
x
∴ x2 = 4 .
∴ x =2,
x =-2 (不合题意,舍去)
y = ,
4
x
当x=2时 ,
y =2 ,
∴点P的坐标为
(2,2).
本节课学习了哪些知识
在知识应用过程中需要注意什么 你有什么收获
课堂小结
1.如图,点B在反比例函数y= (x>0)的图象
上,过点B分别向x轴、y轴作垂线,垂足分
别为点A,C,则矩形OABC的面积是 .
巩固提高
O
x
B
y
A
C
5
x
5
2.如图是反比例函数y= (k>0)在第一象限
内的图象,点M是图象上一点,MP垂直x轴
于点P,如果△MOP的面积为1,那么k的值
是 _____ .
k
x
O
x
M
y
P
2
3.如图,A,B,C为反比例 函数图象上的三个
点,分别过点 A,B,C向x轴、y轴作垂线,
构成三个矩形,它们的面积分别是 S1,S2,
S3,则S1,S2,S3的大小关系是( ).
A.S1=S2>S3
B. S1C.S1>S2>S3
D.S1=S2=S3
x
O
y
A
B
C
D
4.如图,A,B是反比例数y= 图象上的两点,
分别经过点A,B作x轴、y轴的垂线,构成图
中三个相邻且互不重叠的小矩形,它们的面积
分别为S1,S2,S3.已知S3=1,则S1+S2=( ).
A.3 B. 4
C.5 D.6
O
x
A
B
y
S3
S1
S2
4
x
D
5.如图,在平面直角坐标系中,过点M(- 3,2)
分别作x轴、y轴的垂线,与反比例数y= 图
象交于A,B两点,则S四边形MAOB为( ).
A.8 B. 10
C.12 D.14
4
x
x
O
y
A
B
M
B
今天作业
课本P49页第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.5反比例函数的图象和性质(4)
教学目标:
1.理解反比例函数的比例常数k的几何意义,会用k的几何意义求相关的图形面积;
2.结合实例引导学生理解k的几何意义,是从感性认识到理性认识的转化过程,发展学生的思维.
教学重点:理解和领会反比例函数的几何意义;
教学难点:图象不在第一象限时的线段长的表示.
1.反比例函数的定义
若两个变量x、y之间可以表示成y= ( k是常数,k≠0),则称y是x反比例函数.
反比例函数的解析式可以写成 , 或写成 的形式.它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数 .
k
x
xy=k(k≠0)
y=kx-1
k
复习旧知
2.反比例函数的图象
反比例函数y= (k≠0)的图象是 .
双曲线
k
x
因为x≠0,k≠0,相应地y值也不能为0,所以反比例函数的图象永不与x轴、y轴相交.
x
O
y
x
O
y
3.反比例函数的性质
当k > 0时,图象分布在第 象限,在每个象限内,y随的增大x而 ;
当k < 0时,图象分布在第 象限,在每个象限内,y随x的增大而 .
一、三
减小
二、四
增大
k>0
k < 0
图象
性质
所在
象限
一、三
二、四
在每个象限内,y随x的增大而减小.
在每个象限内,y随x的增大而增大.
y=
k
x
(k≠0)
x
O
y
x
O
y
(x,y同号)
(x,y异号)
反比例函数的图象和性质
反比例函数y= (k≠0)中 k的几何意义:
由双曲线上任意一点向两坐标轴作垂线,两垂线与坐标轴围成的矩形的面积为 .
k
x
|k|
x
O
y
A
B
P
P
x
O
y
A
B
P
P
S矩形PAOB=
=|xy|
=|y|·|x|
=|k|
PA·PB
学习新知
反比例函数y= (k≠0)中 k的几何意义:
由双曲线上任意一点向两坐标轴作垂线,
两垂线与坐标轴围成的矩形的面积为 .
O
y
x
M
N
A(M,N)
k
x
B(P,Q)
P
Q
S矩形AMON
=S矩形BPOQ
=k
|k|
2.点P为反比例函数y= 图象上一个点, 作PQ垂直于x轴,垂足为Q.问△OPQ的面积是否会因点P位置的变化而变化,为什么?
k
x
x
O
y
P
Q
P
S△OPQ
= |xy|
= |y|·|x|
= |k|
= PQ·OQ
1
2
1
2
1
2
1
2
△OPQ的面积不会因点P位置的变化而变化.
Q
练习巩固
3.如图,点A是反比例函数y= (x>0)图象上任意一点, AB平行于x轴交反比例函数y=- (x<0)的图象于点B,作以AB为边的平行四边形ABCD,其顶点C,D在x轴上,则S□ABCD为多少?
2
x
3
x
x
O
y
A
B
C
D
y=
2
x
y=-
3
x
F
E
G
过点A作AE垂直x轴,垂足为E,
过点B作BF垂直x轴,垂足为F,
则有△AED≌△BFC (HL)
x
O
y
A
B
C
D
y=
2
x
y=-
3
x
F
E
G
∴ S□ABCD
=S矩形BFOG
+S矩形AEOG
过点A作AE垂直x轴,垂足为E,
过点B作BF垂直x轴,垂足为F,
则有△AED≌△BFC (HL)
=BF·OF
+ AE·OE
=3+2
=5
5.如图,点A,B是反比例函数y= 图象上的两点,
9
x
x
O
y
A
y=
9
x
B
分别过点A,B作AE作x轴、y轴的垂线,
构成图中的三个相邻且不重叠的小矩形S1,S2,S3.
已知S2=3,求S1+S3的值
S1
S2
S3
解:
∵ S1+S2
=9
S2+S3
=9
∴ S1+2S2+S3
=18
∵ S2=3,
∴ S1+S3
=12.
例1 如图,两个反比例函数 y= 和 y=- 的图象分别是 L1 和 L2.设点 P 在 L1 上,PC⊥x 轴,垂足为 C,交L2 于点 A;PD⊥y 轴,垂足为 D,交L2 于点 B,则△PAB 的面积为( ).
1
x
2
x
A.3 B.4
C. D.5
x
y
P
A
O
B
C
D
L2
L1
9
2
C
(a, )
1
a
(a,- )
2
a
(-2a, )
1
a
PA=
1
a
-
-
2
a
( )
=
3
a
PB =
a
-
-
2a
( )
=3a
x
O
y
A
B
C
D
y=
k
x
y=-
3k
x
P
Q
y=2t
x=t
( ,2t)
k
2t
( ,2t)
-
3k
2t
(t, )
k
t
(t, )
-
3k
t
CD=
-
=
k
2t
( )
-
3k
2t
2k
t
AB=
-
=
k
t
( )
-
3k
t
4k
t
S△PCD
= ·
1
2
2k
t
2t
=2k
S△QAB
= ·
1
2
4k
t
t
=2k
例2 如图,一次函数 y=ax+b 的图象与反比例函数
的图象交于第一象限 C,D 两点,与坐标轴交于
A、B 两点,连接 OC,OD(O 是坐标原点).
① 利用图中条件,求反比例函数的解析式和 m 的值;
② 双曲线上是否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明,并求出点 P 的坐标;若不存在,说明理由.
O
x
A
B
C(1,4)
y
D(4,m)
y=
k
x
∵ 的图象经过点 C(1,4).
例2 如图,一次函数 y=ax+b 的图象与反比例函数
的图象交于第一象限 C,D 两点,与坐标轴交于
A、B 两点,连接 OC,OD(O 是坐标原点).
① 利用图中条件,求反比例函数的解析式和 m 的值;
O
x
A
B
C(1,4)
y
D(4,m)
y=
k
x
y=
k
x
∴ 4 = .
k
1
∴ k =4 .
∴ y = .
4
x
∴当x=4时,
m=
4
4
=1 .
①
② 双曲线上是否存在一点 P,使得△POC 和△POD 的面积相等?若存在,给出证明,并求出点 P 的坐标;若不存在,说明理由.
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ y=ax+b的图象经过点 C(1,4),D(4,1).
a+b =4 ,
4a+b =1 ,
a =-1
∴y =-x+5 ,
∴A(5,0),B(0,5)
∴ OA =OB .
双曲线上存在一点 P,使得△POC和△POD 的面积相等.
∴
b=5.
∴
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ y=ax+b的图象经过点 C(1,4),D(4,1).
∴ a+b =4 ,
4a+b =1 ,
∴ a =-1 ,b=5.
∴y =-x+5 ,
∴A(5,0),B(0,5),
∴ OA =OB .
双曲线上存在一点 P,使得△POC 和△POD 的面积相等.
过点 O作OP⊥AB,交双曲线于点P.
连接PC、PD,
则PC=PD.
∵ OC =OD,OP=OP .
∴ △OPC ≌△OPD .
∴ S△OPC =S△OPD .
O
x
A
B
C(1,4)
y
D(4,m)
P
②
∵ OP⊥AB,
yAB =-x+5 ,
∴ yOP =x
∵ y=x,
∴ x = .
4
x
∴ x2 = 4 .
∴ x =2,
x =-2 (不合题意,舍去)
y = ,
4
x
当x=2时 ,
y =2 ,
∴点P的坐标为
(2,2).
本节课学习了哪些知识
在知识应用过程中需要注意什么 你有什么收获
课堂小结
1.如图,点B在反比例函数y= (x>0)的图象
上,过点B分别向x轴、y轴作垂线,垂足分
别为点A,C,则矩形OABC的面积是 .
巩固提高
O
x
B
y
A
C
5
x
5
2.如图是反比例函数y= (k>0)在第一象限
内的图象,点M是图象上一点,MP垂直x轴
于点P,如果△MOP的面积为1,那么k的值
是 _____ .
k
x
O
x
M
y
P
2
3.如图,A,B,C为反比例 函数图象上的三个
点,分别过点 A,B,C向x轴、y轴作垂线,
构成三个矩形,它们的面积分别是 S1,S2,
S3,则S1,S2,S3的大小关系是( ).
A.S1=S2>S3
B. S1
D.S1=S2=S3
x
O
y
A
B
C
D
4.如图,A,B是反比例数y= 图象上的两点,
分别经过点A,B作x轴、y轴的垂线,构成图
中三个相邻且互不重叠的小矩形,它们的面积
分别为S1,S2,S3.已知S3=1,则S1+S2=( ).
A.3 B. 4
C.5 D.6
O
x
A
B
y
S3
S1
S2
4
x
D
5.如图,在平面直角坐标系中,过点M(- 3,2)
分别作x轴、y轴的垂线,与反比例数y= 图
象交于A,B两点,则S四边形MAOB为( ).
A.8 B. 10
C.12 D.14
4
x
x
O
y
A
B
M
B
今天作业
课本P49页第4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
