沪科版数学七年级上册 4.5.2补(余)角 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 4.5.2补(余)角 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
4.5 角的比较与补(余)角
第2课时 补(余)角
第4章 直线与角
知识要点
1.余角和补角
2.余角、补角的性质
新知导入
想一想:观察下图中的角,想一想它们之间存在怎样的数量关系。
新知导入
想一想:观察下图中的角,想一想它们之间存在怎样的数量关系。
课程讲授
1
余角和补角
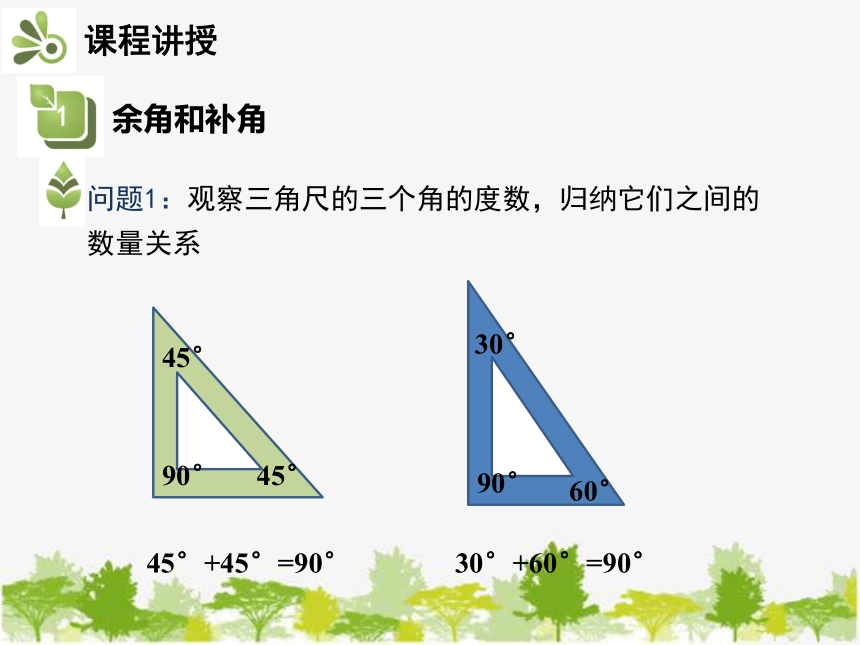
问题1:观察三角尺的三个角的度数,归纳它们之间的数量关系
60°
90°
30°
90°
45°
45°
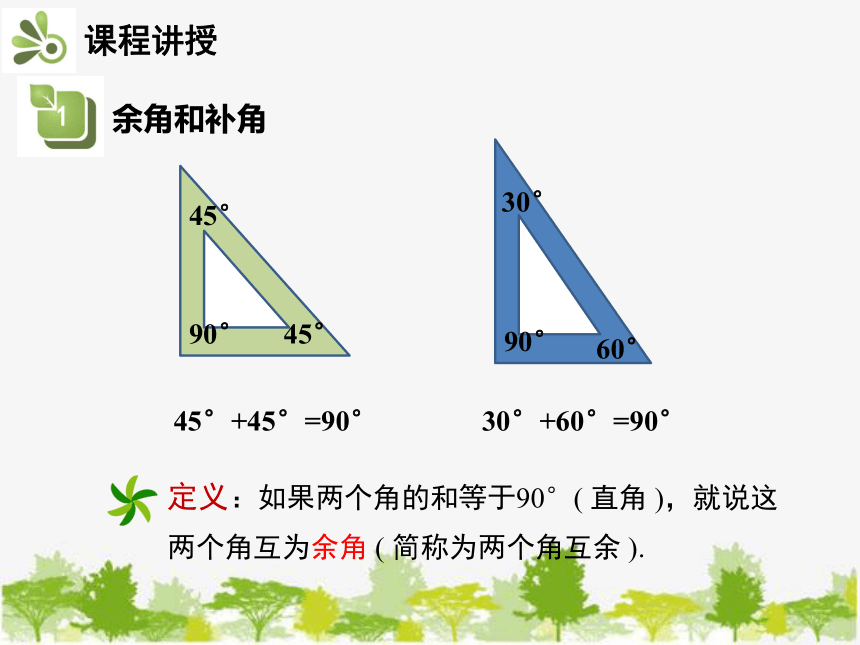
45°+45°=90°
30°+60°=90°
课程讲授
1
余角和补角
60°
90°
30°
90°
45°
45°
45°+45°=90°
30°+60°=90°
定义:如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
课程讲授
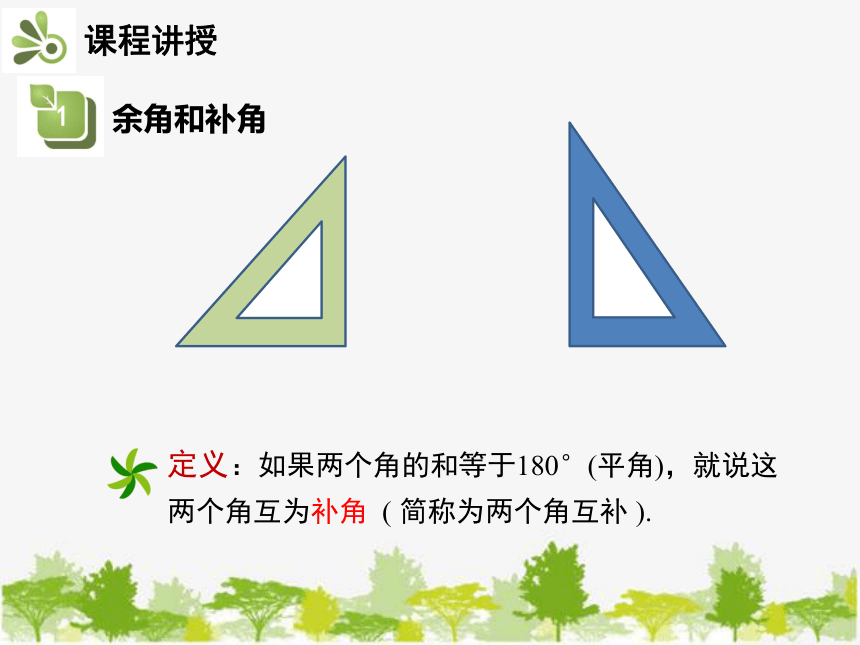
定义:如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
1
余角和补角
课程讲授
练一练:已知∠α=35°,那么∠α的余角等于( )
A.35°
B.55°
C.65°
D.145°
B
1
余角和补角
课程讲授
2
余角、补角的性质
问题1:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
3
∠2=180°-∠1
∠3=180°-∠1
∠2=∠3
课程讲授
2
余角、补角的性质
余角的性质:
同角 (等角) 的补角相等.
补角的性质:
同角 (等角) 的余角相等.
课程讲授
2
余角、补角的性质
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
C
D
E
解:因为点A,O,B在同一直线上,所以 ∠AOC 和 ∠BOC 互为补角.
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以
∠COD+∠COE= ∠AOC+ ∠BOC
2
1
2
1
= (∠AOC+∠BOC ) = 90°.
2
1
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
课程讲授
2
余角、补角的性质
例2 如图,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
29.66°
60.34°
30.17°
解:因为∠AOB与∠BOD互为余角,
所以∠BOD = 90°-∠AOB
= 90°-29.66°= 60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以
课程讲授
2
余角、补角的性质
例3 已知一个角的余角是这个角的补角的三分之一,
求这个角的度数
解:设这个角为x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得
解得 x = 45.
因此,这个角的度数为45°.
课程讲授
练一练:如图,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD的度数为( )
A.35°
B.45°
C.55°
D.65°
C
2
余角、补角的性质
随堂练习
1.若∠A=34°,则∠A的补角的度数为( )
A.56°
B.146°
C.156°
D.166°
B
随堂练习
2.下列说法正确的是( )
A.一个角的余角一定是钝角
B.一个角的补角一定是钝角
C.锐角的余角一定是锐角
D.锐角的补角一定是锐角
C
随堂练习
3.将一副直角三角尺按如图所示放置,若∠AOD=20°,则∠BOC的大小为( )
A.140°
B.160°
C.170°
D.150°
B
随堂练习
4.已知岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )
D
课堂小结
余角和补角
余角和补角的定义
余角和补角的性质
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
4.5 角的比较与补(余)角
第2课时 补(余)角
第4章 直线与角
知识要点
1.余角和补角
2.余角、补角的性质
新知导入
想一想:观察下图中的角,想一想它们之间存在怎样的数量关系。
新知导入
想一想:观察下图中的角,想一想它们之间存在怎样的数量关系。
课程讲授
1
余角和补角
问题1:观察三角尺的三个角的度数,归纳它们之间的数量关系
60°
90°
30°
90°
45°
45°
45°+45°=90°
30°+60°=90°
课程讲授
1
余角和补角
60°
90°
30°
90°
45°
45°
45°+45°=90°
30°+60°=90°
定义:如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
课程讲授
定义:如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
1
余角和补角
课程讲授
练一练:已知∠α=35°,那么∠α的余角等于( )
A.35°
B.55°
C.65°
D.145°
B
1
余角和补角
课程讲授
2
余角、补角的性质
问题1:∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
3
∠2=180°-∠1
∠3=180°-∠1
∠2=∠3
课程讲授
2
余角、补角的性质
余角的性质:
同角 (等角) 的补角相等.
补角的性质:
同角 (等角) 的余角相等.
课程讲授
2
余角、补角的性质
例1 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
C
D
E
解:因为点A,O,B在同一直线上,所以 ∠AOC 和 ∠BOC 互为补角.
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以
∠COD+∠COE= ∠AOC+ ∠BOC
2
1
2
1
= (∠AOC+∠BOC ) = 90°.
2
1
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
课程讲授
2
余角、补角的性质
例2 如图,∠AOB与∠BOD互为余角,OC是∠BOD的平分线,∠AOB=29.66°,求∠COD的度数.
29.66°
60.34°
30.17°
解:因为∠AOB与∠BOD互为余角,
所以∠BOD = 90°-∠AOB
= 90°-29.66°= 60.34°.
又因为OC是∠BOD的平分线,
因此,∠COD 的度数为 30.17°.
所以
课程讲授
2
余角、补角的性质
例3 已知一个角的余角是这个角的补角的三分之一,
求这个角的度数
解:设这个角为x°,则这个角的余角为(90-x)°,
补角为(180-x)°.
根据题意,得
解得 x = 45.
因此,这个角的度数为45°.
课程讲授
练一练:如图,已知∠BOC=55°,∠AOC=∠BOD=90°,则∠AOD的度数为( )
A.35°
B.45°
C.55°
D.65°
C
2
余角、补角的性质
随堂练习
1.若∠A=34°,则∠A的补角的度数为( )
A.56°
B.146°
C.156°
D.166°
B
随堂练习
2.下列说法正确的是( )
A.一个角的余角一定是钝角
B.一个角的补角一定是钝角
C.锐角的余角一定是锐角
D.锐角的补角一定是锐角
C
随堂练习
3.将一副直角三角尺按如图所示放置,若∠AOD=20°,则∠BOC的大小为( )
A.140°
B.160°
C.170°
D.150°
B
随堂练习
4.已知岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )
D
课堂小结
余角和补角
余角和补角的定义
余角和补角的性质
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如果两个角的和等于180°(平角),就说这两个角互为补角 ( 简称为两个角互补 ).
同角 (等角) 的补角相等.
同角 (等角) 的余角相等.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
