高中数学人教A版(2019)选择性必修第一册单元过关卷——第一章空间向量与立体几何A(有答案)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第一册单元过关卷——第一章空间向量与立体几何A(有答案) | 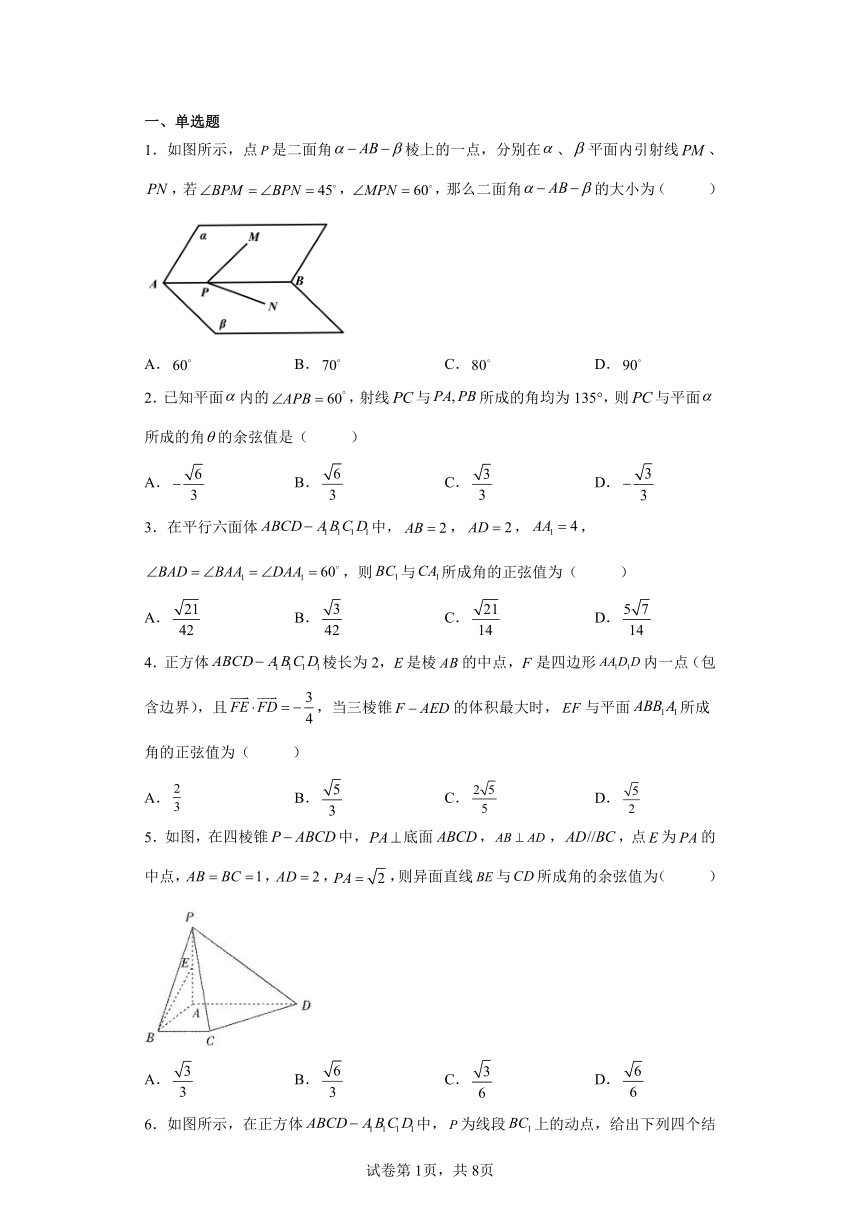 | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 10:44:58 | ||
图片预览





文档简介
一、单选题
1.如图所示,点是二面角棱上的一点,分别在、平面内引射线、,若,,那么二面角的大小为( )
A. B. C. D.
2.已知平面内的,射线与所成的角均为135°,则与平面所成的角的余弦值是( )
A. B. C. D.
3.在平行六面体中,,,,,则与所成角的正弦值为( )
A. B. C. D.
4.正方体棱长为2,是棱的中点,是四边形内一点(包含边界),且,当三棱锥的体积最大时,与平面所成角的正弦值为( )
A. B. C. D.
5.如图,在四棱锥中,底面,,,点为的中点,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
6.如图所示,在正方体中,为线段上的动点,给出下列四个结论:①DP长度为定值;②三棱锥的体积为定值;③任意点P,都有;④存在点P,使得平面其中正确的是( )
A.①③ B.②④ C.②③ D.①④
7.在棱长为2的正四面体ABCD中,点M满足=x+y-(x+y-1),点N满足=λ+(1-λ),当AM、BN最短时,·=( )
A.- B. C.- D.
8.如图,正方体的棱长为a,E是棱的动点,则下列说法正确的( )个.
①若E为的中点,则直线平面
②三棱锥的体积为定值
③E为的中点时,直线与平面所成的角正切值为
④过点,C,E的截面的面积的范围是
A.1 B.2 C.3 D.4
二、多选题
9.设是空间一个基底,下列选项中正确的是( )
A.若,,则
B.则两两共面,但不可能共面
C.对空间任一向量,总存在有序实数组,使
D.则,,一定能构成空间的一个基底
10.在平行六面体中,,,则下列说法正确的是( )
A.线段的长度为
B.异面直线夹角的余弦值为
C.对角面的面积为
D.平行六面体的体积为
11.已知ABCD﹣A1B1C1D1为正方体,下列说法中正确的是( )
A.
B.
C.向量与向量的夹角是60°
D.正方体ABCD﹣A1B1C1D1的体积为
12.正方体的棱长为,,,分别为,,的中点.则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点与点到平面的距离相等
三、填空题
13.如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为_____.
14.如图所示,三棱锥的侧棱长都相等,底面与侧面都是以为斜边的等腰直角三角形,为线段的中点,为直线上的动点,若平面与平面所成锐二面角的平面角为,则的最大值为_________.
15.如图,多面体中,面为正方形,平面,,且,,为棱的中点,为棱上的动点,有下列结论:
①当为棱的中点时,平面;
②存在点,使得;
③三棱锥的体积为定值;
④三棱锥的外接球表面积为.
其中正确的结论序号为______.(填写所有正确结论的序号)
16.在直三棱柱中,,二面角的大小为,点到平面的距离为,点到平面的距离为,则异面直线与所成角的余弦值为_______.
四、解答题
17.如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
18.如图,在正方体中, E为的中点.
(Ⅰ)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值.
19.如图1,四棱锥中,底面,底面是直角梯形,,,,,,,为侧棱上靠近点的四等分点.
(1)证明:平面;
(2)求二面角的平面角的余弦值.
20.如图所示,在直三棱柱中,,,,.
(1)求证:;
(2)在上是否存在点,使得平面,若存在,确定点位置并说明理由,若不存在,说明理由.
21.如图所示,在直三棱柱中,侧面为长方形,,,,.
(1)求证:平面平面;
(2)求直线和平面所成角的正弦值;
(3)在线段上是否存在一点T,使得点T到直线的距离是,若存在求的长,不存在说明理由.
22.如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】过上一点分别在、内做的垂线,交、于点、,则即为二面角的平面角,设,通过解三角形即可求出答案.
【详解】解:过上一点分别在、内做的垂线,交、于点、,
则即为二面角的平面角,如下图所示:
设,∵,
∴,,
又∵,∴为等边三角形,则,
∴,
∴,
故选:D.
2.B
【分析】作出图形,如图,通过分析,可得为与平面所成的角的补角,利用余弦定理可以计算.
【详解】作出如下图形,令,则,,
取中点,连接,则即为与平面所成的角的补角,
在中,,
在中,,
,
,
与平面所成的角的余弦值是.
故选:B.
【点睛】本题考查线面角的求法,找出所成角,构造三角形是解题的关键.
3.D
【分析】先利用基底表示向量,再利用向量的夹角公式求解.
【详解】解:,
则,
,
,
,
,
,
所以,
故选:D
4.A
【分析】建立空间直角坐标系,设出,利用向量的数量积及体积最大值求得,从而得到与平面所成角的正弦值.
【详解】如图,以A为坐标原点,AB,AD,所在直线分别为轴,建立空间直角坐标系,
则,,,设,,
则,
由于为定值,要想三棱锥的体积最大,则F到底面ADE的距离最大,
其中,
所以当时,取得最大值,
因为,
所以的最大值为,
所以,,
平面的法向量,
所以与平面所成角的正弦值为
故选:A
5.A
【分析】建立空间直角坐标,根据条件写出相关点的坐标,再求出向量,的坐标,再根据向量的夹角公式计算即可.
【详解】以为原点,以,,所在直线分别为轴、轴、轴,
建立如图所示的空间直角坐标系,
则,,,,
,,
,
则异面直线与所成角的余弦值为,
故选:A.
6.C
【分析】设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间中两点间的距离公式可判断①的正误,利用锥体的体积公式可判断②的正误,利用空间向量法可判断③④的正误.
【详解】如下图所示:
设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、、、、、,设点,其中.
对于①,不是定值,①错误;
对于②, 在正方体中,且,
所以,四边形为平行四边形,则,
平面,平面,则平面,
,则点到平面的距离为定值,而的面积也为定值,
所以,三棱锥的体积为定值,②正确;
对于③,,,所以,,
因此,对任意点,都有,③正确;
对于④,,,,
,这样的不存在,所以,不存在点,使得平面,④错误.
故选:C.
【点睛】关键点点睛:本题的关键在于建系,设出点的坐标,然后根据向量的运算求解判断.
7.A
【分析】首先由向量的关系式得M∈平面BCD,N∈直线AC,由条件判断点,线,面的位置关系,结合向量数量积的运算,即可求解.
【详解】由共面向量定理和共线向量定理可知,M∈平面BCD,N∈直线AC,当AM、BN最短时,AM⊥平面BCD,BN⊥AC,
所以M为△BCD的中心,N为AC的中点,
此时,2||==,∴||=,
∵AM⊥平面BCD,MC 平面BCD,
∴AM⊥MC,
∴||=
==.
又=(+),
∴·=(·+·)
=-||2=-.
故选:A.
8.B
【分析】如图,以A为原点,AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,对于①、③、④利用向量法计算证明;对于②利用等体积法计算即可判断.
【详解】如图,以A为原点,AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,
则B(a,0,0),C(a,a,0),D(0,a,0),,.
所以,.
对于①:当E为的中点时,.设平面的一个法向量为,
则,不妨令x =1,则,
所以平面A1BD的一个法向量为.
又因为,所以与不垂直,所以直线平面不成立.故①错误;
对于②:三棱锥的体积等于三棱锥的体积.
又,高为a,所以.故②错误;
对于③:当E为的中点时,.平面的一个法向量为,
而.
设直线B1E与平面所成的角为,所以.
所以,所以,
即直线与平面所成的角正切值为.故③正确;
对于④:设.因为,,
所以在上得到投影为.
所以点E到直线的距离为.
当z=0,即D、E重合时,截面为矩形,其面积为.
当时,截面为等腰梯形.设截面交于F.所以,
高,所以其面积为.
记,
所以,所以在上单调递减函数,
所以,即.
因为,所以
当z=a,即D1、E重合时,截面为边长为的正三角形,其面积为.
综上所述:.故④正确.
故选:B
9.BCD
【解析】根据空间向量的基底的概念,对选项逐一分析,可得正确选项.
【详解】由是空间一个基底,知:
在A中,若,,则与的夹角不一定是,故A错误;
在B中,两两共面,但不可能共面,故B正确;
在C中,根据空间向量的基本定理可知C正确;
在D中,因为不共面,假设,,共面,设,化简得,可得共面,与已知矛盾,所以,,不共面,可作为基底,故D正确.
故选:BCD.
【点睛】本题主要考查向量的基底的概念,需要注意:
(1)如果是基底,则一定不共面;
(2)对空间中任意向量,都可以用基底向量进行表示;
(3)如果,则共面.
10.AD
【分析】设,求得,根据,求得的值,可判定A正确;由,可判定B错误;由为正三角形,根据,得到对角面为矩形,可判定C错误;由,可判定D正确.
【详解】设,则,
对于A中,因为,
可得,
所以A正确;
对于B中,因为,
可得异面直线与夹角的余弦值为0,所以B错误;
对于C中,因为,所以为正三角形,可得,
因为,所以,
所以对角面为矩形,其面积为,所以C错误;
对于D中,设与交于点,连接,取的中点,连接,
可得,所以D正确.
故选:AD.
11.AB
【分析】根据正方体ABCD﹣A1B1C1D1的特征,利用空间向量的线性运算以及数量积公式即可求解.
【详解】由题意,正方体ABCD﹣A1B1C1D1如下图所示:
由向量的加法得到:,
∵,∴,所以A正确;
∵,AB1⊥A1C,∴,故B正确;
∵△ACD1是等边三角形,∴∠AD1C=60°,
又∵A1BD1C,
∴异面直线AD1与A1B所成的夹角为60°,
但是向量与向量的夹角是120°,故C错误;
∵AB⊥AA1,∴,
故0,故D错误.
故选:AB.
12.BC
【分析】由,得出平面,进而得出,可判断A;取的中点,连接,利用线面平行的判定定理,可判断B;连接,,得到平面为平面截正方体所得的截面,再计算其面积即可判断C;利用反证法即可判断D.
【详解】对于A,若,
因为且,所以平面,
所以,所以,此时不成立,所以线与直线不垂直,故A错误;
对于B,如图所示,取的中点,连接,
由条件可知:,且,
又平面,平面,平面,平面,
∴平面,平面,又,
所以平面平面,又因为平面,
所以平面,故B正确;
对于C,因为为的中点,所以,
所以四点共面,所以截面即为梯形,
由题得该等腰梯形的上底下底,腰长为,所以梯形面积为,故C正确;
对于D,假设与到平面的距离相等,即平面将平分,则平面必过的中点,连接交于,而不是中点,则假设不成立,故D错误.
故选:BC.
13.4
【解析】以为坐标原点,所在直线分别为轴,轴,轴建立空间直角坐标系, 设,求出平面的一个法向量,则,则可以得到答案.
【详解】解:以为坐标原点,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
设,则,,,故,,,
设平面的一个法向量为,则,可取,
故,
又直线与平面所成角的正弦值为,
,解得.
故答案为:4.
【点睛】本题考查根据线面角,利用向量法求柱体的高,属于中档题.
14.
【分析】由题设可得构建为原点的空间直角坐标系,根据已知标注相关点的坐标,设,,,可得的坐标,进而求面与面的法向量,利用空间向量夹角的坐标表示得到关于的表达式,由二次函数的性质即可求其最大值.
【详解】底面与侧面都是以为斜边的等腰直角三角形,则≌,
∴,设,则,
∵为的中点,则,
∴,即,
以为原点,如图建立空间直角坐标系,则、、、,
设,,,则,而,,
∴、、,
∴,
∴、、、,
设面的一个法向量,则,
即,令,则,
设面的一个法向量 ,则,即,
令,则,
面与面所成锐二面角的平面角为,则,
当时 ,即的最大值为.
故答案为:.
15.①③④
【分析】根据线面平行的判定定理,以及线线垂直的判定,结合棱锥体积的计算公式,以及棱锥外接球半径的求解,对每一项进行逐一求解和分析即可.
【详解】对①:当H为DE的中点时,取中点为,连接,
因为分别为的中点,
故可得//,,
根据已知条件可知://,
故//,
故四边形为平行四边形,则//,又平面平面,
故//面,故①正确;
对②:因为平面平面,
故,
又四边形为矩形,
故,则两两垂直,
以为坐标原点,建立空间直角坐标系如图所示:
则,设,,
若GH⊥AE,则,
即,解得,不满足题意,故②错误;
对③:,因为均为定点,故为定值,
又//平面平面,
故//面,
又点在上运动,故点到平面的距离是定值,
故三棱锥的体积为定值,则③正确;
对④:由题可得平面,又面为正方形,
∴,
∴AB⊥平面BCF,则AB,BC,CF两两垂直,
∴AF为三棱锥的外接球的直径,
又,
∴三棱锥的外接球表面积为,故④正确.
故答案为:①③④.
16.
【分析】根据二面角的定义可得,再由点到面的距离可得,,,,建立空间直角坐标系,求出各点坐标,利用空间向量夹角公式即可求解.
【详解】因为三棱柱是直三棱柱,所以面,
因为面, 面,所以,,
所以即为二面角的平面角,所以,
点到平面的距离为,点到平面的距离为,
由面面垂直的性质可得: 点到平面的距离为,点到平面的距离为,
因为,所以,,
由余弦定理可得:,
可得,
因为,所以,
如图:以为原点,分别以,,所在的直线为,,轴建立空间直角坐标系,则,,,,
所以,
,.
.
所以异面直线与所成角的余弦值为.
故答案为:.
17.(1)见解析;(2).
【分析】(1)利用三角形中位线和可证得,证得四边形为平行四边形,进而证得,根据线面平行判定定理可证得结论;(2)以菱形对角线交点为原点可建立空间直角坐标系,通过取中点,可证得平面,得到平面的法向量;再通过向量法求得平面的法向量,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
【详解】(1)连接,
,分别为,中点 为的中位线
且
又为中点,且 且
四边形为平行四边形
,又平面,平面
平面
(2)设,
由直四棱柱性质可知:平面
四边形为菱形
则以为原点,可建立如下图所示的空间直角坐标系:
则:,,,D(0,-1,0)
取中点,连接,则
四边形为菱形且 为等边三角形
又平面,平面
平面,即平面
为平面的一个法向量,且
设平面的法向量,又,
,令,则,
二面角的正弦值为:
【点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系,从而通过求解法向量夹角的余弦值来得到二面角的正弦值,属于常规题型.
18.(Ⅰ)证明见解析;(Ⅱ).
【分析】(Ⅰ)证明出四边形为平行四边形,可得出,然后利用线面平行的判定定理可证得结论;也可利用空间向量计算证明;
(Ⅱ)可以将平面扩展,将线面角转化,利用几何方法作出线面角,然后计算;也可以建立空间直角坐标系,利用空间向量计算求解 .
【详解】(Ⅰ)[方法一]:几何法
如下图所示:
在正方体中,且,且,
且,所以,四边形为平行四边形,则,
平面,平面,平面;
[方法二]:空间向量坐标法
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
设正方体的棱长为,则、、、,,,
设平面的法向量为,由,得,
令,则,,则.
又∵向量,,
又平面,平面;
(Ⅱ)[方法一]:几何法
延长到,使得,连接,交于,
又∵,∴四边形为平行四边形,∴,
又∵,∴,所以平面即平面,
连接,作,垂足为,连接,
∵平面,平面,∴,
又∵,∴直线平面,
又∵直线平面,∴平面平面,
∴在平面中的射影在直线上,∴直线为直线在平面中的射影,∠为直线与平面所成的角,
根据直线直线,可知∠为直线与平面所成的角.
设正方体的棱长为2,则,,∴,
∴,
∴,
即直线与平面所成角的正弦值为.
[方法二]:向量法
接续(I)的向量方法,求得平面平面的法向量,
又∵,∴,
∴直线与平面所成角的正弦值为.
[方法三]:几何法+体积法
如图,设的中点为F,延长,易证三线交于一点P.
因为,
所以直线与平面所成的角,即直线与平面所成的角.
设正方体的棱长为2,在中,易得,
可得.
由,得,
整理得.
所以.
所以直线与平面所成角的正弦值为.
[方法四]:纯体积法
设正方体的棱长为2,点到平面的距离为h,
在中,,
,
所以,易得.
由,得,解得,
设直线与平面所成的角为,所以.
【整体点评】(Ⅰ)的方法一使用线面平行的判定定理证明,方法二使用空间向量坐标运算进行证明;
(II)第一种方法中使用纯几何方法,适合于没有学习空间向量之前的方法,有利用培养学生的集合论证和空间想象能力,第二种方法使用空间向量方法,两小题前后连贯,利用计算论证和求解,定为最优解法;方法三在几何法的基础上综合使用体积方法,计算较为简洁;方法四不作任何辅助线,仅利用正余弦定理和体积公式进行计算,省却了辅助线和几何的论证,不失为一种优美的方法.
19.(1)证明见解析
(2)
【分析】(1)取上取一点,使,连接、,证明出四边形为平行四边形,可得出,再利用线面平行的判定定理可证得结论成立;
(2)以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间向量法可求得二面角的平面角的余弦值.
(1)
证明:取上取一点,使,连接、,
由题知,所以,.
又因为,,所以,,
所以四边形为平行四边形,所以.
因为平面,平面,所以直线平面.
(2)
解:因为平面,,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
所以、、、、,
设平面的法向量为,,,
则,取,则,
易知平面的一个法向量为,
所以,,
由图可知,二面角的平面角为锐角,故二面角的余弦值为.
20.(1)证明见解析;
(2)在上存在点使得平面,且为的中点.
【分析】(1)本题首先以为坐标原点建立空间直角坐标系,然后得出、,最后根据即可证得;
(2)本题可假设点存在,则,然后通过得出,最后求出的值,即可得出结论.
(1)
因为,,,所以,
如图所示,在直三棱柱中,以为坐标原点,直线、、分别为轴、轴、轴,建立空间直角坐标系,
则,,,,,
因为,,
所以,,即.
(2)
若存在点使平面,则,,
,,,,
因为平面,所以存在实数、,使成立,
则,解得,
故在上存在点使平面,此时点为中点.
21.(1)证明见解析
(2)
(3)存在,
【解析】(1)
由于,所以,
根据直三棱柱的性质可知,由于,所以平面,
由于平面,所以平面平面.
(2)
设N是的中点,连接,则,MA,MB,MN,两两相互垂直.
以M为空间坐标原点建立如图所示空间直角坐标系,
,,
设平面的法向量为,
则,令,可得,
设直线和平面所成角为,则;
(3)
设,则,
过T作,则,
∵,
∴,
∴,∴或(舍)
∴.
22.(1)证明见解析;(2).
【分析】(1)首先将平面进行扩展,然后结合所得的平面与直线的交点即可证得题中的结论;
(2)建立空间直角坐标系,利用空间直角坐标系求得相应平面的法向量,然后解方程即可求得实数的值.
【详解】(1)如图所示,取的中点,连结,
由于为正方体,为中点,故,
从而四点共面,即平面CDE即平面,
据此可得:直线交平面于点,
当直线与平面相交时只有唯一的交点,故点与点重合,
即点为中点.
(2)以点为坐标原点,方向分别为轴,轴,轴正方向,建立空间直角坐标系,
不妨设正方体的棱长为2,设,
则:,
从而:,
设平面的法向量为:,则:
,
令可得:,
设平面的法向量为:,则:
,
令可得:,
从而:,
则:,
整理可得:,故(舍去).
【点睛】本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
答案第1页,共2页
答案第1页,共2页
1.如图所示,点是二面角棱上的一点,分别在、平面内引射线、,若,,那么二面角的大小为( )
A. B. C. D.
2.已知平面内的,射线与所成的角均为135°,则与平面所成的角的余弦值是( )
A. B. C. D.
3.在平行六面体中,,,,,则与所成角的正弦值为( )
A. B. C. D.
4.正方体棱长为2,是棱的中点,是四边形内一点(包含边界),且,当三棱锥的体积最大时,与平面所成角的正弦值为( )
A. B. C. D.
5.如图,在四棱锥中,底面,,,点为的中点,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
6.如图所示,在正方体中,为线段上的动点,给出下列四个结论:①DP长度为定值;②三棱锥的体积为定值;③任意点P,都有;④存在点P,使得平面其中正确的是( )
A.①③ B.②④ C.②③ D.①④
7.在棱长为2的正四面体ABCD中,点M满足=x+y-(x+y-1),点N满足=λ+(1-λ),当AM、BN最短时,·=( )
A.- B. C.- D.
8.如图,正方体的棱长为a,E是棱的动点,则下列说法正确的( )个.
①若E为的中点,则直线平面
②三棱锥的体积为定值
③E为的中点时,直线与平面所成的角正切值为
④过点,C,E的截面的面积的范围是
A.1 B.2 C.3 D.4
二、多选题
9.设是空间一个基底,下列选项中正确的是( )
A.若,,则
B.则两两共面,但不可能共面
C.对空间任一向量,总存在有序实数组,使
D.则,,一定能构成空间的一个基底
10.在平行六面体中,,,则下列说法正确的是( )
A.线段的长度为
B.异面直线夹角的余弦值为
C.对角面的面积为
D.平行六面体的体积为
11.已知ABCD﹣A1B1C1D1为正方体,下列说法中正确的是( )
A.
B.
C.向量与向量的夹角是60°
D.正方体ABCD﹣A1B1C1D1的体积为
12.正方体的棱长为,,,分别为,,的中点.则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点与点到平面的距离相等
三、填空题
13.如图,在正四棱柱中,底面边长为2,直线与平面所成角的正弦值为,则正四棱柱的高为_____.
14.如图所示,三棱锥的侧棱长都相等,底面与侧面都是以为斜边的等腰直角三角形,为线段的中点,为直线上的动点,若平面与平面所成锐二面角的平面角为,则的最大值为_________.
15.如图,多面体中,面为正方形,平面,,且,,为棱的中点,为棱上的动点,有下列结论:
①当为棱的中点时,平面;
②存在点,使得;
③三棱锥的体积为定值;
④三棱锥的外接球表面积为.
其中正确的结论序号为______.(填写所有正确结论的序号)
16.在直三棱柱中,,二面角的大小为,点到平面的距离为,点到平面的距离为,则异面直线与所成角的余弦值为_______.
四、解答题
17.如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
18.如图,在正方体中, E为的中点.
(Ⅰ)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值.
19.如图1,四棱锥中,底面,底面是直角梯形,,,,,,,为侧棱上靠近点的四等分点.
(1)证明:平面;
(2)求二面角的平面角的余弦值.
20.如图所示,在直三棱柱中,,,,.
(1)求证:;
(2)在上是否存在点,使得平面,若存在,确定点位置并说明理由,若不存在,说明理由.
21.如图所示,在直三棱柱中,侧面为长方形,,,,.
(1)求证:平面平面;
(2)求直线和平面所成角的正弦值;
(3)在线段上是否存在一点T,使得点T到直线的距离是,若存在求的长,不存在说明理由.
22.如图:在正方体中,为中点,与平面交于点.
(1)求证:为的中点;
(2)点是棱上一点,且二面角的余弦值为,求的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】过上一点分别在、内做的垂线,交、于点、,则即为二面角的平面角,设,通过解三角形即可求出答案.
【详解】解:过上一点分别在、内做的垂线,交、于点、,
则即为二面角的平面角,如下图所示:
设,∵,
∴,,
又∵,∴为等边三角形,则,
∴,
∴,
故选:D.
2.B
【分析】作出图形,如图,通过分析,可得为与平面所成的角的补角,利用余弦定理可以计算.
【详解】作出如下图形,令,则,,
取中点,连接,则即为与平面所成的角的补角,
在中,,
在中,,
,
,
与平面所成的角的余弦值是.
故选:B.
【点睛】本题考查线面角的求法,找出所成角,构造三角形是解题的关键.
3.D
【分析】先利用基底表示向量,再利用向量的夹角公式求解.
【详解】解:,
则,
,
,
,
,
,
所以,
故选:D
4.A
【分析】建立空间直角坐标系,设出,利用向量的数量积及体积最大值求得,从而得到与平面所成角的正弦值.
【详解】如图,以A为坐标原点,AB,AD,所在直线分别为轴,建立空间直角坐标系,
则,,,设,,
则,
由于为定值,要想三棱锥的体积最大,则F到底面ADE的距离最大,
其中,
所以当时,取得最大值,
因为,
所以的最大值为,
所以,,
平面的法向量,
所以与平面所成角的正弦值为
故选:A
5.A
【分析】建立空间直角坐标,根据条件写出相关点的坐标,再求出向量,的坐标,再根据向量的夹角公式计算即可.
【详解】以为原点,以,,所在直线分别为轴、轴、轴,
建立如图所示的空间直角坐标系,
则,,,,
,,
,
则异面直线与所成角的余弦值为,
故选:A.
6.C
【分析】设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间中两点间的距离公式可判断①的正误,利用锥体的体积公式可判断②的正误,利用空间向量法可判断③④的正误.
【详解】如下图所示:
设正方体的棱长为,以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,
则、、、、、、、,设点,其中.
对于①,不是定值,①错误;
对于②, 在正方体中,且,
所以,四边形为平行四边形,则,
平面,平面,则平面,
,则点到平面的距离为定值,而的面积也为定值,
所以,三棱锥的体积为定值,②正确;
对于③,,,所以,,
因此,对任意点,都有,③正确;
对于④,,,,
,这样的不存在,所以,不存在点,使得平面,④错误.
故选:C.
【点睛】关键点点睛:本题的关键在于建系,设出点的坐标,然后根据向量的运算求解判断.
7.A
【分析】首先由向量的关系式得M∈平面BCD,N∈直线AC,由条件判断点,线,面的位置关系,结合向量数量积的运算,即可求解.
【详解】由共面向量定理和共线向量定理可知,M∈平面BCD,N∈直线AC,当AM、BN最短时,AM⊥平面BCD,BN⊥AC,
所以M为△BCD的中心,N为AC的中点,
此时,2||==,∴||=,
∵AM⊥平面BCD,MC 平面BCD,
∴AM⊥MC,
∴||=
==.
又=(+),
∴·=(·+·)
=-||2=-.
故选:A.
8.B
【分析】如图,以A为原点,AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,对于①、③、④利用向量法计算证明;对于②利用等体积法计算即可判断.
【详解】如图,以A为原点,AB,AD,AA1所在直线为x,y,z轴建立空间直角坐标系,
则B(a,0,0),C(a,a,0),D(0,a,0),,.
所以,.
对于①:当E为的中点时,.设平面的一个法向量为,
则,不妨令x =1,则,
所以平面A1BD的一个法向量为.
又因为,所以与不垂直,所以直线平面不成立.故①错误;
对于②:三棱锥的体积等于三棱锥的体积.
又,高为a,所以.故②错误;
对于③:当E为的中点时,.平面的一个法向量为,
而.
设直线B1E与平面所成的角为,所以.
所以,所以,
即直线与平面所成的角正切值为.故③正确;
对于④:设.因为,,
所以在上得到投影为.
所以点E到直线的距离为.
当z=0,即D、E重合时,截面为矩形,其面积为.
当时,截面为等腰梯形.设截面交于F.所以,
高,所以其面积为.
记,
所以,所以在上单调递减函数,
所以,即.
因为,所以
当z=a,即D1、E重合时,截面为边长为的正三角形,其面积为.
综上所述:.故④正确.
故选:B
9.BCD
【解析】根据空间向量的基底的概念,对选项逐一分析,可得正确选项.
【详解】由是空间一个基底,知:
在A中,若,,则与的夹角不一定是,故A错误;
在B中,两两共面,但不可能共面,故B正确;
在C中,根据空间向量的基本定理可知C正确;
在D中,因为不共面,假设,,共面,设,化简得,可得共面,与已知矛盾,所以,,不共面,可作为基底,故D正确.
故选:BCD.
【点睛】本题主要考查向量的基底的概念,需要注意:
(1)如果是基底,则一定不共面;
(2)对空间中任意向量,都可以用基底向量进行表示;
(3)如果,则共面.
10.AD
【分析】设,求得,根据,求得的值,可判定A正确;由,可判定B错误;由为正三角形,根据,得到对角面为矩形,可判定C错误;由,可判定D正确.
【详解】设,则,
对于A中,因为,
可得,
所以A正确;
对于B中,因为,
可得异面直线与夹角的余弦值为0,所以B错误;
对于C中,因为,所以为正三角形,可得,
因为,所以,
所以对角面为矩形,其面积为,所以C错误;
对于D中,设与交于点,连接,取的中点,连接,
可得,所以D正确.
故选:AD.
11.AB
【分析】根据正方体ABCD﹣A1B1C1D1的特征,利用空间向量的线性运算以及数量积公式即可求解.
【详解】由题意,正方体ABCD﹣A1B1C1D1如下图所示:
由向量的加法得到:,
∵,∴,所以A正确;
∵,AB1⊥A1C,∴,故B正确;
∵△ACD1是等边三角形,∴∠AD1C=60°,
又∵A1BD1C,
∴异面直线AD1与A1B所成的夹角为60°,
但是向量与向量的夹角是120°,故C错误;
∵AB⊥AA1,∴,
故0,故D错误.
故选:AB.
12.BC
【分析】由,得出平面,进而得出,可判断A;取的中点,连接,利用线面平行的判定定理,可判断B;连接,,得到平面为平面截正方体所得的截面,再计算其面积即可判断C;利用反证法即可判断D.
【详解】对于A,若,
因为且,所以平面,
所以,所以,此时不成立,所以线与直线不垂直,故A错误;
对于B,如图所示,取的中点,连接,
由条件可知:,且,
又平面,平面,平面,平面,
∴平面,平面,又,
所以平面平面,又因为平面,
所以平面,故B正确;
对于C,因为为的中点,所以,
所以四点共面,所以截面即为梯形,
由题得该等腰梯形的上底下底,腰长为,所以梯形面积为,故C正确;
对于D,假设与到平面的距离相等,即平面将平分,则平面必过的中点,连接交于,而不是中点,则假设不成立,故D错误.
故选:BC.
13.4
【解析】以为坐标原点,所在直线分别为轴,轴,轴建立空间直角坐标系, 设,求出平面的一个法向量,则,则可以得到答案.
【详解】解:以为坐标原点,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
设,则,,,故,,,
设平面的一个法向量为,则,可取,
故,
又直线与平面所成角的正弦值为,
,解得.
故答案为:4.
【点睛】本题考查根据线面角,利用向量法求柱体的高,属于中档题.
14.
【分析】由题设可得构建为原点的空间直角坐标系,根据已知标注相关点的坐标,设,,,可得的坐标,进而求面与面的法向量,利用空间向量夹角的坐标表示得到关于的表达式,由二次函数的性质即可求其最大值.
【详解】底面与侧面都是以为斜边的等腰直角三角形,则≌,
∴,设,则,
∵为的中点,则,
∴,即,
以为原点,如图建立空间直角坐标系,则、、、,
设,,,则,而,,
∴、、,
∴,
∴、、、,
设面的一个法向量,则,
即,令,则,
设面的一个法向量 ,则,即,
令,则,
面与面所成锐二面角的平面角为,则,
当时 ,即的最大值为.
故答案为:.
15.①③④
【分析】根据线面平行的判定定理,以及线线垂直的判定,结合棱锥体积的计算公式,以及棱锥外接球半径的求解,对每一项进行逐一求解和分析即可.
【详解】对①:当H为DE的中点时,取中点为,连接,
因为分别为的中点,
故可得//,,
根据已知条件可知://,
故//,
故四边形为平行四边形,则//,又平面平面,
故//面,故①正确;
对②:因为平面平面,
故,
又四边形为矩形,
故,则两两垂直,
以为坐标原点,建立空间直角坐标系如图所示:
则,设,,
若GH⊥AE,则,
即,解得,不满足题意,故②错误;
对③:,因为均为定点,故为定值,
又//平面平面,
故//面,
又点在上运动,故点到平面的距离是定值,
故三棱锥的体积为定值,则③正确;
对④:由题可得平面,又面为正方形,
∴,
∴AB⊥平面BCF,则AB,BC,CF两两垂直,
∴AF为三棱锥的外接球的直径,
又,
∴三棱锥的外接球表面积为,故④正确.
故答案为:①③④.
16.
【分析】根据二面角的定义可得,再由点到面的距离可得,,,,建立空间直角坐标系,求出各点坐标,利用空间向量夹角公式即可求解.
【详解】因为三棱柱是直三棱柱,所以面,
因为面, 面,所以,,
所以即为二面角的平面角,所以,
点到平面的距离为,点到平面的距离为,
由面面垂直的性质可得: 点到平面的距离为,点到平面的距离为,
因为,所以,,
由余弦定理可得:,
可得,
因为,所以,
如图:以为原点,分别以,,所在的直线为,,轴建立空间直角坐标系,则,,,,
所以,
,.
.
所以异面直线与所成角的余弦值为.
故答案为:.
17.(1)见解析;(2).
【分析】(1)利用三角形中位线和可证得,证得四边形为平行四边形,进而证得,根据线面平行判定定理可证得结论;(2)以菱形对角线交点为原点可建立空间直角坐标系,通过取中点,可证得平面,得到平面的法向量;再通过向量法求得平面的法向量,利用向量夹角公式求得两个法向量夹角的余弦值,进而可求得所求二面角的正弦值.
【详解】(1)连接,
,分别为,中点 为的中位线
且
又为中点,且 且
四边形为平行四边形
,又平面,平面
平面
(2)设,
由直四棱柱性质可知:平面
四边形为菱形
则以为原点,可建立如下图所示的空间直角坐标系:
则:,,,D(0,-1,0)
取中点,连接,则
四边形为菱形且 为等边三角形
又平面,平面
平面,即平面
为平面的一个法向量,且
设平面的法向量,又,
,令,则,
二面角的正弦值为:
【点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系,从而通过求解法向量夹角的余弦值来得到二面角的正弦值,属于常规题型.
18.(Ⅰ)证明见解析;(Ⅱ).
【分析】(Ⅰ)证明出四边形为平行四边形,可得出,然后利用线面平行的判定定理可证得结论;也可利用空间向量计算证明;
(Ⅱ)可以将平面扩展,将线面角转化,利用几何方法作出线面角,然后计算;也可以建立空间直角坐标系,利用空间向量计算求解 .
【详解】(Ⅰ)[方法一]:几何法
如下图所示:
在正方体中,且,且,
且,所以,四边形为平行四边形,则,
平面,平面,平面;
[方法二]:空间向量坐标法
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
设正方体的棱长为,则、、、,,,
设平面的法向量为,由,得,
令,则,,则.
又∵向量,,
又平面,平面;
(Ⅱ)[方法一]:几何法
延长到,使得,连接,交于,
又∵,∴四边形为平行四边形,∴,
又∵,∴,所以平面即平面,
连接,作,垂足为,连接,
∵平面,平面,∴,
又∵,∴直线平面,
又∵直线平面,∴平面平面,
∴在平面中的射影在直线上,∴直线为直线在平面中的射影,∠为直线与平面所成的角,
根据直线直线,可知∠为直线与平面所成的角.
设正方体的棱长为2,则,,∴,
∴,
∴,
即直线与平面所成角的正弦值为.
[方法二]:向量法
接续(I)的向量方法,求得平面平面的法向量,
又∵,∴,
∴直线与平面所成角的正弦值为.
[方法三]:几何法+体积法
如图,设的中点为F,延长,易证三线交于一点P.
因为,
所以直线与平面所成的角,即直线与平面所成的角.
设正方体的棱长为2,在中,易得,
可得.
由,得,
整理得.
所以.
所以直线与平面所成角的正弦值为.
[方法四]:纯体积法
设正方体的棱长为2,点到平面的距离为h,
在中,,
,
所以,易得.
由,得,解得,
设直线与平面所成的角为,所以.
【整体点评】(Ⅰ)的方法一使用线面平行的判定定理证明,方法二使用空间向量坐标运算进行证明;
(II)第一种方法中使用纯几何方法,适合于没有学习空间向量之前的方法,有利用培养学生的集合论证和空间想象能力,第二种方法使用空间向量方法,两小题前后连贯,利用计算论证和求解,定为最优解法;方法三在几何法的基础上综合使用体积方法,计算较为简洁;方法四不作任何辅助线,仅利用正余弦定理和体积公式进行计算,省却了辅助线和几何的论证,不失为一种优美的方法.
19.(1)证明见解析
(2)
【分析】(1)取上取一点,使,连接、,证明出四边形为平行四边形,可得出,再利用线面平行的判定定理可证得结论成立;
(2)以点为坐标原点,、、所在直线分别为、、轴建立空间直角坐标系,利用空间向量法可求得二面角的平面角的余弦值.
(1)
证明:取上取一点,使,连接、,
由题知,所以,.
又因为,,所以,,
所以四边形为平行四边形,所以.
因为平面,平面,所以直线平面.
(2)
解:因为平面,,
以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
所以、、、、,
设平面的法向量为,,,
则,取,则,
易知平面的一个法向量为,
所以,,
由图可知,二面角的平面角为锐角,故二面角的余弦值为.
20.(1)证明见解析;
(2)在上存在点使得平面,且为的中点.
【分析】(1)本题首先以为坐标原点建立空间直角坐标系,然后得出、,最后根据即可证得;
(2)本题可假设点存在,则,然后通过得出,最后求出的值,即可得出结论.
(1)
因为,,,所以,
如图所示,在直三棱柱中,以为坐标原点,直线、、分别为轴、轴、轴,建立空间直角坐标系,
则,,,,,
因为,,
所以,,即.
(2)
若存在点使平面,则,,
,,,,
因为平面,所以存在实数、,使成立,
则,解得,
故在上存在点使平面,此时点为中点.
21.(1)证明见解析
(2)
(3)存在,
【解析】(1)
由于,所以,
根据直三棱柱的性质可知,由于,所以平面,
由于平面,所以平面平面.
(2)
设N是的中点,连接,则,MA,MB,MN,两两相互垂直.
以M为空间坐标原点建立如图所示空间直角坐标系,
,,
设平面的法向量为,
则,令,可得,
设直线和平面所成角为,则;
(3)
设,则,
过T作,则,
∵,
∴,
∴,∴或(舍)
∴.
22.(1)证明见解析;(2).
【分析】(1)首先将平面进行扩展,然后结合所得的平面与直线的交点即可证得题中的结论;
(2)建立空间直角坐标系,利用空间直角坐标系求得相应平面的法向量,然后解方程即可求得实数的值.
【详解】(1)如图所示,取的中点,连结,
由于为正方体,为中点,故,
从而四点共面,即平面CDE即平面,
据此可得:直线交平面于点,
当直线与平面相交时只有唯一的交点,故点与点重合,
即点为中点.
(2)以点为坐标原点,方向分别为轴,轴,轴正方向,建立空间直角坐标系,
不妨设正方体的棱长为2,设,
则:,
从而:,
设平面的法向量为:,则:
,
令可得:,
设平面的法向量为:,则:
,
令可得:,
从而:,
则:,
整理可得:,故(舍去).
【点睛】本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
答案第1页,共2页
答案第1页,共2页
