21.4实际问题与二次函数(4) 课件(共35张PPT)
文档属性
| 名称 | 21.4实际问题与二次函数(4) 课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-15 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
沪科版 九年级上册
21.4实际问题与二次函数(4)
二次函数是单变量最优化问题的数学模型,如生活中涉及的求最大利润,最大面积等.这体现了数学的实 用性,是理论与实践结合的集中体现.本节课主要来 研究利润问题.
课件说明
x
y
O
b
2a
-
x=
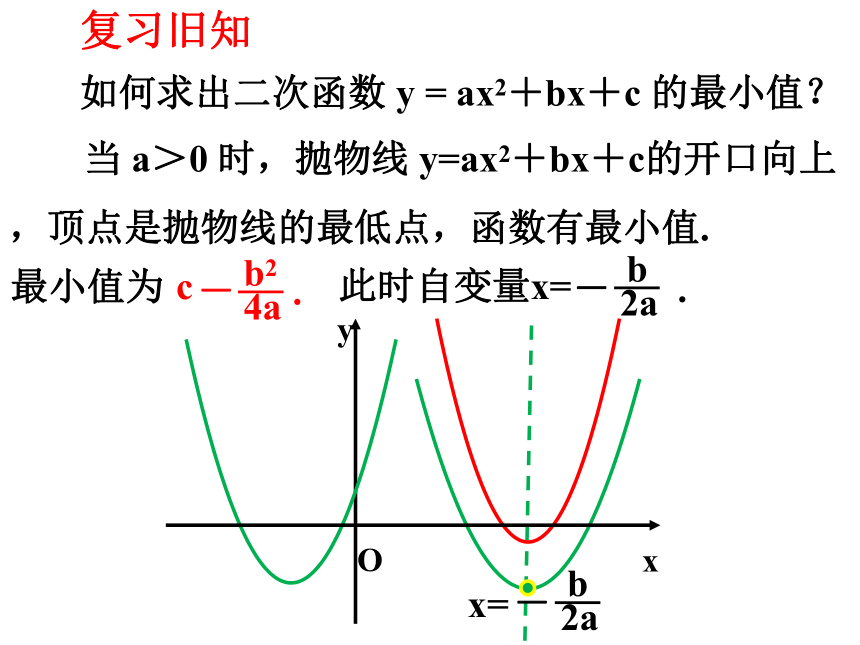
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
c
b2
4a
- .
最小值为
如何求出二次函数 y = ax2+bx+c 的最小值?
此时自变量x=
b
2a
- .
复习旧知
x
y
O
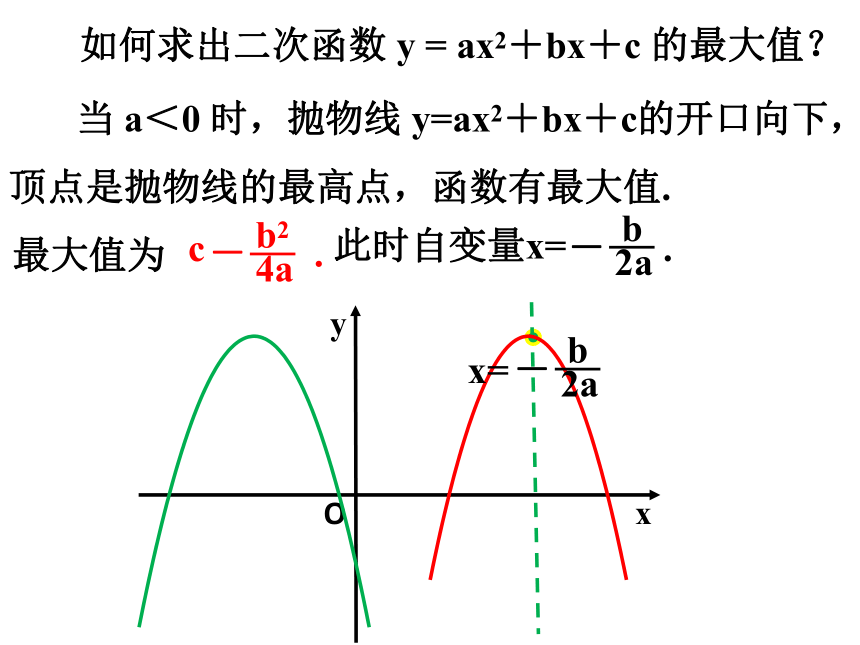
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
- .
最大值为
如何求出二次函数 y = ax2+bx+c 的最大值?
此时自变量x=
b
2a
- .
b
2a
-
x=
求出下列函数的最大值或最小值,并求出相应的x值.
① y= x2- x+2, ② y=(x+1)(2 - x)
解:
①
∴函数有最小值,
相应的x值为
b
2a
-
=
∵ a=
=
-
1
2
∴最小值y=
=
c
b2
4a
-
=
2-
3
3
3
> 0,
∵ b=- , c=2
3
(- )2
4×
3
3
4
3
2-
x =
-
2×
3
3
求出下列函数的最大值或最小值,并求出相应的x值.
① y= x2- x+2, ② y=(x+1)(2-x)
解:
∴函数有最大值,
相应的x值为
b
2a
-
=
∵ a=
=
-
1
2
∴最大值y=
=
c
b2
4a
-
=
2-
3
3
-1
< 0,
∵ b= 1 , c=2
2
4×
(-1)
1
4
9
x =
(-1)
2×
1
②
整理,得,
y =-x2+x+2
1.小李在今年的校运动会跳远比赛中跳出了满 意
一跳.函数h=3.5t-4.9t2(t的单位s,h的单位:m)
可以描述他跳跃时重心高度的变化,则他起跳
后到重心最高时所用的时间约是( ).
A.0.71 s B.0.70 s C.0.63 s D.0.36 s
D
2.某商店销售一种练习本,所获利润y元与销售
单价x元之间的关系为y=-2x + 8x+40,则
所获利润最多为( ).
A.36元 B.40元 C.48元 D.44元
C
例4.行驶中的汽车,在制动后由于惯性作用,还要继续往前滑行一段距离才能停止,这段距离称为“制动距离”。为了测定某型号汽车的制动性能,对其进行了测试,测得数据如下表:
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
现有一辆该型号汽车在公路上发生了交通事故,现场测得制动距离为46.5m.则交通事故发生时车速是多少?是否因超速(该段公路最高限速为110km/h)行驶导致了交通事故?
制动时车速 0 10 20 30 40 50
要解答例4这个问题,就是要解决在知道了制动距离时,如何求得相应的制动时车速。因此,可以把制动时的车速看作是制动距离的函数。题中通过列表法给出了几组制动距离与制动时车速有关系的数据,为此,求出制动距离与制动时车速的函数关系式是解答本题的关键。推断问题,它要经历哪些解题过程呢?
从列表数据 函数图象 解析式
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
制动时车速 0 10 20 30 40 50
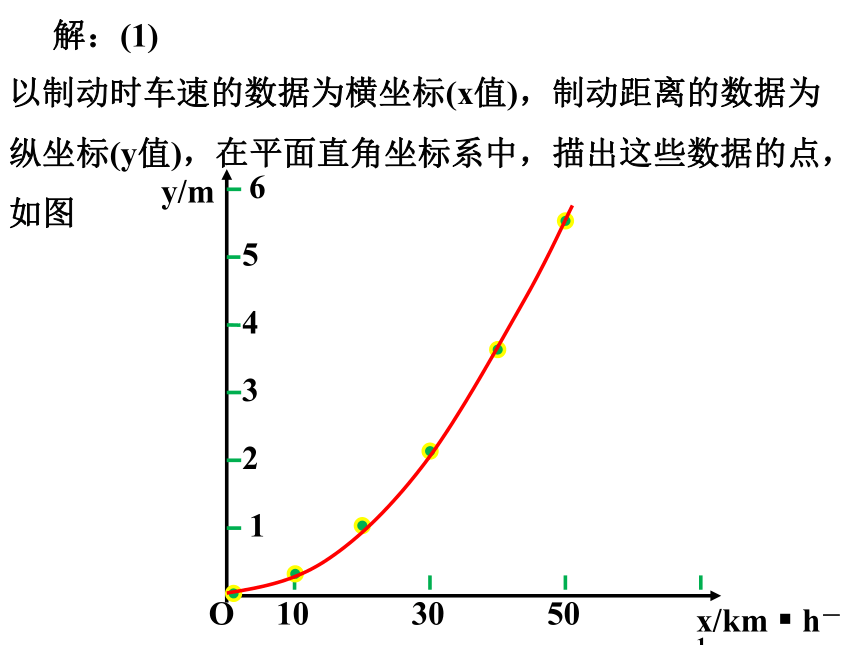
以制动时车速的数据为横坐标(x值),制动距离的数据为纵坐标(y值),在平面直角坐标系中,描出这些数据的点,如图
解:(1)
x/km h-1
y/m
O
2
4
3
10
30
50
1
5
6
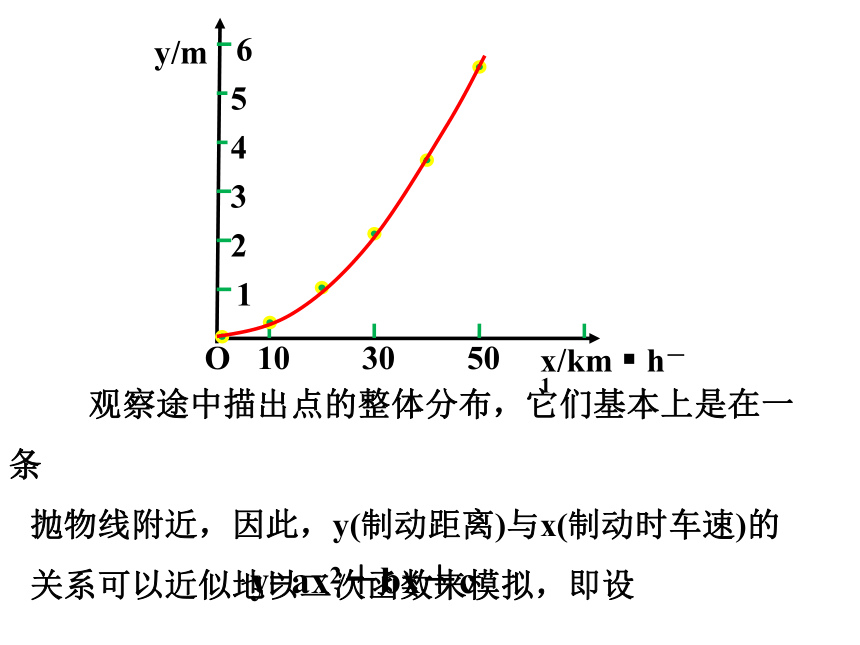
观察途中描出点的整体分布,它们基本上是在一条
抛物线附近,因此,y(制动距离)与x(制动时车速)的
关系可以近似地以二次函数来模拟,即设
y=ax2+bx+c
x/km h-1
y/m
O
2
4
3
10
30
50
1
5
6
y(制动距离)与x(制动时车速)的关系可以近似地以二次函数来模拟,即设
在已知数据中,任选三组,
y=ax2+bx+c
如取(0,0)、(10,0.3)、(20,1.0)
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
制动时车速 0 10 20 30 40 50
分别代入所设函数关系式.
在已知数据中,任选三组,如取(0,0)、(10,0.3)、(20,1.0)分别代入所设函数关系式,得
y=ax2+bx+c
c=0
100a+10b+c=0.3
400a+20b+c=1.0
200a+20b=0.6
400a+20b=1.0
∴
a=0.002
c=0
b=0.01
∴所求函数的表达式为
y=0.002x2+0.01x
把y=46.5m代入y=0.002x2+0.01x,得
解方程,得
x1=150(km/h),x2= -155(km/h)(舍去)
因而,制动46.5m代入函数关系式,得
时车速为150km/h(>110km/h),
即在事故发生时,该车属超速行驶.
0.002x2+0.01x=46.5
2x2+10x=46500
x2+5x=23250
(x-150)(x+155)=0
0.002x2+0.01x=46.5
150
155
-
1
1
x2+5x-23250=0
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
(1)写出图中表示的种植
成本Q元/kg与时间t天
之间的函数表达式 ;
(2)西红柿上市多少天其
种植成本最低?
最低成本是多少?
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
Q=at2+bt+c
(1)设种植成本Q元/kg与
时间t天之间的函数表达式
为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
Q=at2+bt+c
(1)设种植成本Q元/kg与时间t天之间的函数表达式为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
c=2.125
∴
a=0.00005
b=-0.015
⑤-④
①
②
③
③-①
60000a+200b=0
③-②
40000a+100b=0.5
30000a+100b=0
④
⑤
10000a=0.5
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
Q=at2+bt+c
(1)设种植成本Q元/kg与时间t天之间的函数表达式为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
c=2.125
∴
a=0.00005
b=-0.015
∴所求函数的表达式为
Q=0.00005t2 - 0.015t+2.125
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
(2)西红柿上市多少天其
种植成本最低?
最低成本是多少?
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
(2)西红柿上市多少天其种植成本最低?
最低成本是多少?
Q=0.00005t2 - 0.015t+2.125
∴函数有最小值.
∵ a= 0.00005
> 0,
∵ b=-0.015 ,c=2. 125
(2)
相应的t值为
=150
-
∴最小值Q=
2.125-
2
4×
0.00005
(-0.015)
=1
t =
0.00005
2×
-0.015
∴西红柿上市150天其种植成本最低;
最低成本是1元.
(1)这节课学习了用什么知识解决哪类问题? (2)解决问题的一般步骤是什么?应注意哪些问题? (3)你学到了哪些思考问题的方法?
课堂小结
今天作业
课本P58页第11题
现实问题数学化的典型范例
数学花絮
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点
这个线图不能一笔画成
因此,不能不重复地一次走遍这七座桥.
A
B
C
D
什么是一笔画呢
通俗地说,就是笔不离开纸面,能将线图上每一条线都画到而又不重复.
譬如'双钱牌”商标图案就是个一笔画.
怎样来判别是一笔画或不是一笔画呢
如果把线图中偶数条线的交叉点叫做偶点,把奇数条线的交叉点叫做奇点,则有:
若线图中奇点数目不大于2个,这个线图就是一笔画,否则就不是一笔画.
A
B
C
D
奇点
奇点
奇点
奇点
4个奇点>2
∴不是一笔画.
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
21.4实际问题与二次函数(4)
二次函数是单变量最优化问题的数学模型,如生活中涉及的求最大利润,最大面积等.这体现了数学的实 用性,是理论与实践结合的集中体现.本节课主要来 研究利润问题.
课件说明
x
y
O
b
2a
-
x=
当 a>0 时,抛物线 y=ax2+bx+c的开口向上,顶点是抛物线的最低点,函数有最小值.
c
b2
4a
- .
最小值为
如何求出二次函数 y = ax2+bx+c 的最小值?
此时自变量x=
b
2a
- .
复习旧知
x
y
O
当 a<0 时,抛物线 y=ax2+bx+c的开口向下,顶点是抛物线的最高点,函数有最大值.
c
b2
4a
- .
最大值为
如何求出二次函数 y = ax2+bx+c 的最大值?
此时自变量x=
b
2a
- .
b
2a
-
x=
求出下列函数的最大值或最小值,并求出相应的x值.
① y= x2- x+2, ② y=(x+1)(2 - x)
解:
①
∴函数有最小值,
相应的x值为
b
2a
-
=
∵ a=
=
-
1
2
∴最小值y=
=
c
b2
4a
-
=
2-
3
3
3
> 0,
∵ b=- , c=2
3
(- )2
4×
3
3
4
3
2-
x =
-
2×
3
3
求出下列函数的最大值或最小值,并求出相应的x值.
① y= x2- x+2, ② y=(x+1)(2-x)
解:
∴函数有最大值,
相应的x值为
b
2a
-
=
∵ a=
=
-
1
2
∴最大值y=
=
c
b2
4a
-
=
2-
3
3
-1
< 0,
∵ b= 1 , c=2
2
4×
(-1)
1
4
9
x =
(-1)
2×
1
②
整理,得,
y =-x2+x+2
1.小李在今年的校运动会跳远比赛中跳出了满 意
一跳.函数h=3.5t-4.9t2(t的单位s,h的单位:m)
可以描述他跳跃时重心高度的变化,则他起跳
后到重心最高时所用的时间约是( ).
A.0.71 s B.0.70 s C.0.63 s D.0.36 s
D
2.某商店销售一种练习本,所获利润y元与销售
单价x元之间的关系为y=-2x + 8x+40,则
所获利润最多为( ).
A.36元 B.40元 C.48元 D.44元
C
例4.行驶中的汽车,在制动后由于惯性作用,还要继续往前滑行一段距离才能停止,这段距离称为“制动距离”。为了测定某型号汽车的制动性能,对其进行了测试,测得数据如下表:
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
现有一辆该型号汽车在公路上发生了交通事故,现场测得制动距离为46.5m.则交通事故发生时车速是多少?是否因超速(该段公路最高限速为110km/h)行驶导致了交通事故?
制动时车速 0 10 20 30 40 50
要解答例4这个问题,就是要解决在知道了制动距离时,如何求得相应的制动时车速。因此,可以把制动时的车速看作是制动距离的函数。题中通过列表法给出了几组制动距离与制动时车速有关系的数据,为此,求出制动距离与制动时车速的函数关系式是解答本题的关键。推断问题,它要经历哪些解题过程呢?
从列表数据 函数图象 解析式
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
制动时车速 0 10 20 30 40 50
以制动时车速的数据为横坐标(x值),制动距离的数据为纵坐标(y值),在平面直角坐标系中,描出这些数据的点,如图
解:(1)
x/km h-1
y/m
O
2
4
3
10
30
50
1
5
6
观察途中描出点的整体分布,它们基本上是在一条
抛物线附近,因此,y(制动距离)与x(制动时车速)的
关系可以近似地以二次函数来模拟,即设
y=ax2+bx+c
x/km h-1
y/m
O
2
4
3
10
30
50
1
5
6
y(制动距离)与x(制动时车速)的关系可以近似地以二次函数来模拟,即设
在已知数据中,任选三组,
y=ax2+bx+c
如取(0,0)、(10,0.3)、(20,1.0)
制动距离/m 0 0.3 1.0 2.1 3.6 5.5
制动时车速 0 10 20 30 40 50
分别代入所设函数关系式.
在已知数据中,任选三组,如取(0,0)、(10,0.3)、(20,1.0)分别代入所设函数关系式,得
y=ax2+bx+c
c=0
100a+10b+c=0.3
400a+20b+c=1.0
200a+20b=0.6
400a+20b=1.0
∴
a=0.002
c=0
b=0.01
∴所求函数的表达式为
y=0.002x2+0.01x
把y=46.5m代入y=0.002x2+0.01x,得
解方程,得
x1=150(km/h),x2= -155(km/h)(舍去)
因而,制动46.5m代入函数关系式,得
时车速为150km/h(>110km/h),
即在事故发生时,该车属超速行驶.
0.002x2+0.01x=46.5
2x2+10x=46500
x2+5x=23250
(x-150)(x+155)=0
0.002x2+0.01x=46.5
150
155
-
1
1
x2+5x-23250=0
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
(1)写出图中表示的种植
成本Q元/kg与时间t天
之间的函数表达式 ;
(2)西红柿上市多少天其
种植成本最低?
最低成本是多少?
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
Q=at2+bt+c
(1)设种植成本Q元/kg与
时间t天之间的函数表达式
为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
Q=at2+bt+c
(1)设种植成本Q元/kg与时间t天之间的函数表达式为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
c=2.125
∴
a=0.00005
b=-0.015
⑤-④
①
②
③
③-①
60000a+200b=0
③-②
40000a+100b=0.5
30000a+100b=0
④
⑤
10000a=0.5
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
Q=at2+bt+c
(1)设种植成本Q元/kg与时间t天之间的函数表达式为 :
2500a+50b+c=1.5
22500a+150b+c=1
62500a+250b+c=1.5
c=2.125
∴
a=0.00005
b=-0.015
∴所求函数的表达式为
Q=0.00005t2 - 0.015t+2.125
3.某蔬菜基地种植西红柿,由历年市场行情得知,西红
柿的种植成本Q元/kg与上市时间t天的关系式用如图
的抛物线表示.
(2)西红柿上市多少天其
种植成本最低?
最低成本是多少?
t/天
Q/元 kg-1
O
1
2
1.5
50
150
250
0.5
2.5
(2)西红柿上市多少天其种植成本最低?
最低成本是多少?
Q=0.00005t2 - 0.015t+2.125
∴函数有最小值.
∵ a= 0.00005
> 0,
∵ b=-0.015 ,c=2. 125
(2)
相应的t值为
=150
-
∴最小值Q=
2.125-
2
4×
0.00005
(-0.015)
=1
t =
0.00005
2×
-0.015
∴西红柿上市150天其种植成本最低;
最低成本是1元.
(1)这节课学习了用什么知识解决哪类问题? (2)解决问题的一般步骤是什么?应注意哪些问题? (3)你学到了哪些思考问题的方法?
课堂小结
今天作业
课本P58页第11题
现实问题数学化的典型范例
数学花絮
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点
这个线图不能一笔画成
因此,不能不重复地一次走遍这七座桥.
A
B
C
D
什么是一笔画呢
通俗地说,就是笔不离开纸面,能将线图上每一条线都画到而又不重复.
譬如'双钱牌”商标图案就是个一笔画.
怎样来判别是一笔画或不是一笔画呢
如果把线图中偶数条线的交叉点叫做偶点,把奇数条线的交叉点叫做奇点,则有:
若线图中奇点数目不大于2个,这个线图就是一笔画,否则就不是一笔画.
A
B
C
D
奇点
奇点
奇点
奇点
4个奇点>2
∴不是一笔画.
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
一笔画鉴赏
数学花絮
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
