幂的乘方与积的乘方说课课件[下学期]

课件30张PPT。 武义县新宅初中 周东 幂的乘方与积的乘方一 教材分析
1 教材的地位和作用
本章《整式的运算》是新课标第三学段（7—9年级）数与代数中的重要内容，是从具体数与数的运算过渡到整式与整式的运算，也是从一步步运算到运用公式运算的一个过渡。本节内容是有理数运算的基础，是今后学习整式乘除运算铺垫。同时，本节内容与现实世界的联系紧密，对解决实际问题起着非常重要的作用。
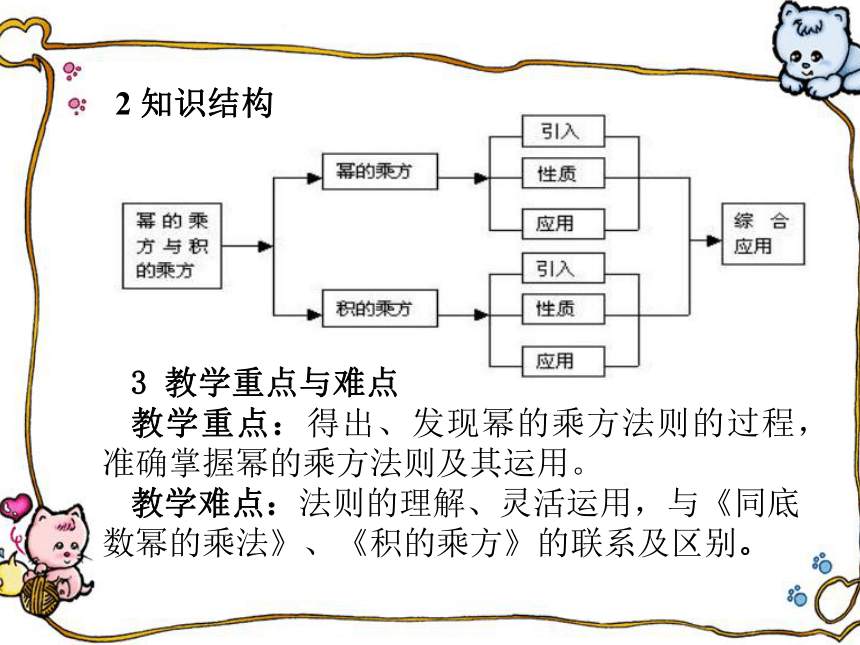
2 知识结构 3 教学重点与难点
教学重点：得出、发现幂的乘方法则的过程，准确掌握幂的乘方法则及其运用。
教学难点：法则的理解、灵活运用，与《同底数幂的乘法》、《积的乘方》的联系及区别。 二、学情分析
七年级学生年龄较小，思维正处在从具体形象思维向抽象逻辑思维转变的阶段。在七年级（上）学生已经学了《有理数的乘方》，认识了有理数乘方运算的意义；在本节课之前，学生又学了《同底数幂的乘法》，这些都为本节课的学习打下了基础。
通过七年级（上）一个学期的学
习，学生已经初步具备了发现问
题，分析、合作、讨论、解决问
题的经验。这为本节课的教学提
供了保证。 三、教学目标
以初步掌握一些有效地表示、处理和交流数量关系以及变化规律，提高运用代数知识与方法解决问题的能力为目标。在教学中教师要现代化教学手段，把传授知识和培养学生良好的数学素养结合起来，为创造性人才的成长打下坚实的基础。因此，结合本节课教材我制定以下教学目标：
知识目标：经历幂的乘方运算性质的过程；理解幂的乘
方性质并能应用它进行有关计算。能力目标：通过推导性质培养学生的抽象思维能力，通
过运用性质；培养学生综合运用知识的能力。情感目标：培养学生严谨的学习态度以及勇于创新的精
神；渗透数学公式的结构美、和谐美。 四、活动设计
组织学生自主发现、分析、讨论、解决问题，在思维受阻，缺乏勇气时，给予适当的引导和鼓励。为完成所定教学目标，特设计以下活动：
1、创设情境，以地球、木星、太阳的半径
和体积的倍数提出问题，引入新课。
2、回顾思考，复习有理数的乘方及同底数
幂的乘法，思考新的问题。
3、合作讨论，分组讨论幂的乘方的意义。
4、理解辨析，通过不同的题型，从不同的
角度加深对公式的理解。 五、教学过程木星地球太阳地球、木星、太阳可以近似地看作球体 .木星、太阳的半径分别约是地球的10倍和102倍，它们的体积分别约是地球的_____倍和 倍.103体积扩大的倍数比半径扩大的倍数大得多.(102)3 如果甲球的半径是乙球的n倍，那么甲球的体积是乙球的n3倍。 回顾 & 思考 a2=
a3=
(102)2=
(102)3=a·aa·a·a102·102=104102·102·102=106????练习&猜想(62)4=
(a2)3=
(am)2=
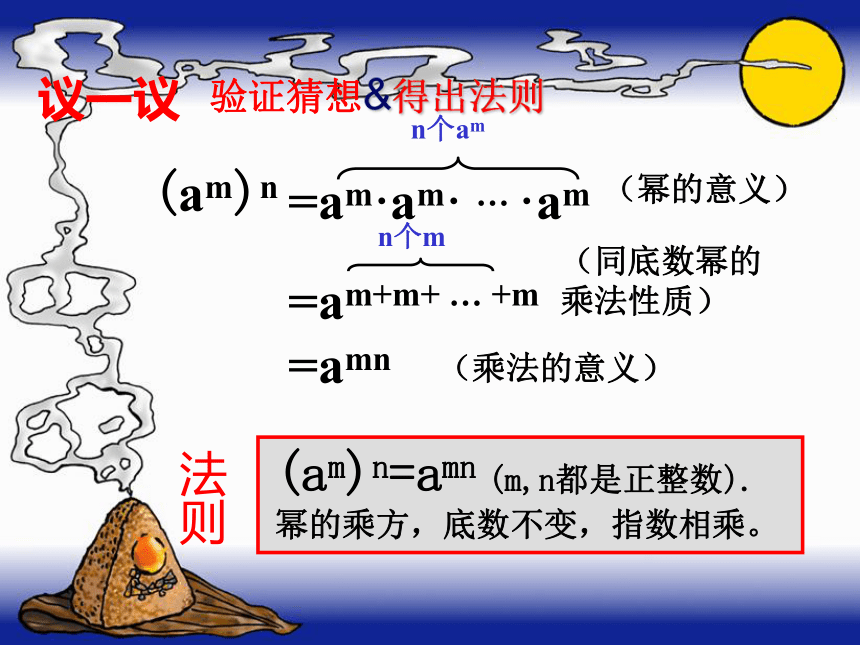
(am)n=62·62·62·62=68a2·a2·a2=a6am·am =a2mamn为什么?为什么?为什么?验证猜想&得出法则(am)n （幂的意义）（同底数幂的乘法性质） =amn （乘法的意义） (am)n=amn (m,n都是正整数).
幂的乘方，底数不变，指数相乘。 议一议法则(1) (107)2 (2) -(y4)m
(3) (x3)2·x
(4) [(x-y)2]3
(5) [(103)4]5
(6) 2(a2)5-(a3)4 试一试&想一想＝107×2＝1014 ＝-y4·m＝-y4m =x3×2·x=x6·x=x7 =(x-y)2×3=(x-y)6 =[103×4]5=[1012]5=1060 =2a2×6－a3×4=2a12－a12=a12 仔细观察,你认为幂的乘方有什么特点? (1)、公式中的底数a可以是具体的数，也可以是代数式。 (2)、注意幂的乘方中底数不变,指数相乘。
而同底数幂的乘法中是底数不变,指数相加。?(3)、多重乘方可以重复运用上述法则，
如［(am)n］p＝(amn)p＝amnp判断&改错 (23)3=26
a3×a3=59
(3) -(x5)2=x10
(4) (yx-1)2=y2x-1
比一比&赛一赛第1题第7题第6题第5题第2题第4题第3题第8题第9题看哪组的 多!第10题第11题第12题 每个组派一名代表参加比赛，第二组代表为第一组代表选题，答对第一组加星，答错第二组加星。以此类推。(1) (103)3 =(12) (x4)3 =(3) -(x3)5 =(4) (a2)3·a5 =(2) (x2)8·(x4)4 =(11) -(xm)5 = （7）[ 2]3 =（8）(xa-1)2=(6) (a2)3·(a3)4 =(9) [(x-y)2]3·(x-y)= (5) (c2)n·cn+1 =(10) (x2n)3m = 1、同底数幂的乘法和幂的乘方的
区别与联系。
2、公式中的底数a可以是具体的
数，也可以是代数式。
3、多重乘方可以重复
运用法则。 谈一谈：这节课你学到了什么？作业：
书本P16，习题1.5六、课堂教学设计说明 数学上的一些基本法则、公式，给出结论再去证明有时会让人觉得枯燥。创设情境，观察现象，猜测原因，容易引起学生的兴趣。?
借鉴其它学科的方法，在学生明确了（am）n的意义后，提问：“你能猜猜（am）n=？”， “为什么？”。引导学生先猜后证，逐步培养学生观察能力、自信心及抽象概括能力。
谢谢指导！